Методы минимизации логических функций

Понятие о полноте системы функций алгебры логики

Система элементарных булевых функций j ₁, j ₂,..., j_m называется функционально полной, если любую функцию алгебры логики можно представить в виде суперпозиции этих функций.

Примером функционально полной системы элементарных булевых функций служит система трех функций: . Это следует из того, что любую функцию алгебры логики можно представить в виде формулы с помощью конъюнкции, дизъюнкции и отрицания (4).

Однако это не единственная функционально полная система. Примерами функционально полных систем элементарных функций также являются:

1)

2)

3) ;

4)

5)

6)

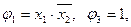
И другие

Доказательством полноты приведенных выше систем элементарных функций может служить возможность сведения любой из них к функционально полной системе из трех элементарных функций .

Минимизация — это процесс приведения булевых функций к такому виду, который допускает наиболее простую, с наименьшим числом элементов, физическую реализацию функции. Частная задача минимизации булевой функции сводится к такому представлению заданной функции, которое содержит наименьшее возможное число букв и наименьшее возможное число операций над ними.

Оценить различные представления одной и той же булевой функции можно по количеству входов логических элементов, реализующих заданную функцию. Такую оценку реализации булевой функции называют ценой реализации булевой функции по Квайну (или ценой покрытия булевой функции системой логических элементов).

Минимизация логических функций может осуществляться различными методами. В качестве таковых выступают:

1) аналитические методы, использующие законы и правила булевой алгебры;

2) метод Квайна, основанный на последовательном применении к парам дизъюнктивных членов логической формулы операций склеивания и элементарного поглощения;

3) карты Карно и диаграммы Вейча, использующие графические представления дизъюнктивных членов.

Аналитические методы, использующие законы и правила булевой алгебры, основаны на равносильных преобразованиях логических формул. Они служат для упрощения формул или приведения их к определённому виду путем использования основных законов алгебры логики.

Под упрощением формулы понимается равносильное преобразование, приводящее к формуле, которая либо содержит по сравнению с исходной меньшее число операций конъюнкции и дизъюнкции и не содержит отрицаний неэлементарных формул, либо содержит меньшее число вхождений переменных.

Некоторые преобразования логических формул похожи на преобразования формул в обычной алгебре (вынесение общего множителя за скобки, использование переместительного и сочетательного законов и т.п.), тогда как другие преобразования основаны на свойствах, которыми не обладают операции обычной алгебры (использование распределительного закона для конъюнкции, законов поглощения, склеивания, де-Моргана и др.).

Примеры приемов и способов, применяемых при упрощении логических формул:

1)

(применяется правило де-Моргана, сочетательный закон, правило операций переменной с её инверсией и правило операций с константами);

2)

(применяется правило де Моргана, выносится за скобки общий множитель, используется правило операций переменной с её инверсией);

3)

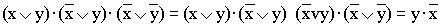
(повторяется второй сомножитель, что разрешено законом идемпотенции; затем комбинируются два первых и два последних сомножителя и используется закон склеивания);

4)

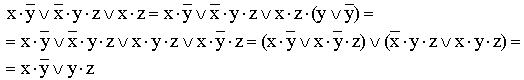
(вводится вспомогательный логический сомножитель ; затем комбинируются два крайних и два средних логических слагаемых и используется закон поглощения);

5)

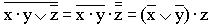
(сначала добиваются, чтобы знак отрицания стоял только перед отдельными переменными, а не перед их комбинациями, для этого дважды применяем правило де-Моргана; затем используем закон двойного отрицания);

6)

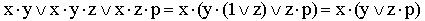
(выносятся за скобки общие множители; применяется правило операций с константами);

7)

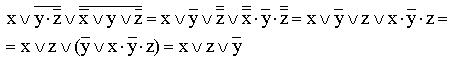
(к отрицаниям неэлементарных формул применяется правило де-Моргана; используются законы двойного отрицания и склеивания);

8)

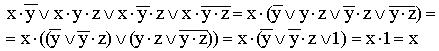
(общий множитель x выносится за скобки, комбинируются слагаемые в скобках — первое с третьим и второе с четвертым, к дизъюнкции применяется правило операции переменной с её инверсией);

9)

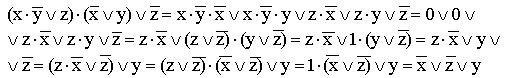
(используются распределительный закон для дизъюнкции, правило операции переменной с ее инверсией, правило операций с константами, переместительный закон и распределительный закон для конъюнкции);

10)

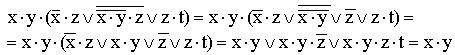
(используются правило де Моргана, закон двойного отрицания и закон поглощения).

Из этих примеров видно, что при упрощении логических формул не всегда очевидно, какой из законов алгебры логики следует применить на том или ином шаге.

Литература:

1. Информатика: Учебник. / Под ред. проф. Н.В.Макаровой. – М.: Финансы и статистика, 2001. с. 124-127.

2. Сергеев Н.П., Вашкевич Н.П. Основы вычислительной техники: Учеб. пособие. – М. Высшая школа, 1988. с. 54-64.

Дата добавления: 2013-12-13