Остаточные члены простейших формул численного дифференцирования

Чтобы получить представление о точности простейших аппроксимаций значений производных в узловых точках, определяемых формулами (20.6) – (20.10), (20.12), будем предполагать, что данная функция f (x) обладает достаточной для выведения остаточных членов гладкостью. Знание структуры приближенных выражений для производных, полученных из интерполяционных соображений, позволяет без особого труда (по крайней мере, для симметричных аппроксимаций) вывести формулы их остаточных членов, манипулируя разложениями f (x) по формуле Тейлора подходящих порядков. Покажем это.

Простейшая несимметричная аппроксимация f¢ (x_i) (формулы первого порядка точности). Запишем представление функции f (x) по формуле Тейлора в окрестности точки x_i:

Выразив отсюда f¢ (x), имеем

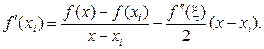(20.13)

Первый член правой части этого равенства – разностное отношение, аппроксимирующее производную вблизи x_i, а второй – остаточный член, характеризующий точность такой аппроксимации. При фиксировании в (20.13) х = x_i одновременно зафиксируется и неизвестная точка ; таким образом, приходим к формуле левой аппроксимации f¢ (x_i) с остаточным членом:

(20.14)

Аналогично при х = x_{i+ 1} из (20.13) получаем формулу правой аппроксимации f¢ (x_i) с остаточным членом:

(20.15)

В приближенных равенствах

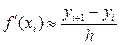(20.16)

при i =0,

(20.17)

при i =1 узнаём выведенные ранее формулы (20.6), (20.7), а остаточные члены в (20.14), (20.15) говорят о том, что, пользуясь аппроксимациями (20.16), (20.17), мы совершаем ошибку O (h), т.е. эти формулы имеют первый порядок точности. Определенную информацию об ошибках левой и правой аппроксимаций первого порядка дает знание знаков остаточных членов.

Простейшая симметричная аппроксимация f¢ (x_i) (формула второго порядка точности). Из разложения

при х = x_{i+ 1} и х = x_{i- 1} имеем соответственно

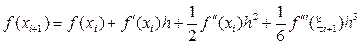
и

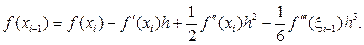
Выполнив почленное вычитание двух последних равенств, получаем

откуда с помощью теоремы о среднем, примененной к сумме третьих производных в квадратных скобках, приходим к формуле симметричной аппроксимации f¢ (x_i) с остаточным членом:

(20.18)

где x _i – некоторая точка интервала (x_{i- 1}, x_{i+ 1}). «Основная» часть формулы (20.18) —

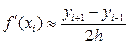(20.19)

a вид ее остаточного члена 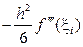означает, что аппроксимация (6.19) имеет второйпорядок точности относительно шага h.

Простейшие аппроксимации второй производной. Из представления

имеем

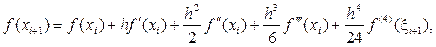
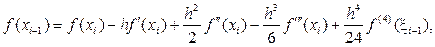
откуда почленным сложением получаем

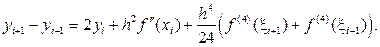
Выражая из последнего равенства , приходим к формуле симметричной аппроксимации с остаточным членом:

(20.20)

Остаточный член этой формулы некоторым характеризует приближенное равенство

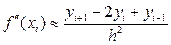(20.21)

как аппроксимацию второй производной в точке х_i, второго порядка точности, т.е. с погрешностью O (h ²).

То же отношение (20.21), используемое в качестве несимметричной аппроксимации второй производной функции f (x), т.е. для вычисления приближенных значений и 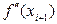дает лишь первый порядок точности.

Дата добавления: 2014-01-04