Свойства равномерно сходящихся рядов

Теорема 40.2. Если функции u_n(x) непрерывны при 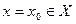и ряд равномерно сходится на Х, то его сумма s(x) тоже непрерывна в точке х₀.

Доказательство.

Выберем ε > 0. Тогда , поэтому существует такой номер п₀, что

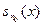- сумма конечного числа непрерывных функций, поэтому 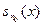непрерывна в точке х₀. Поэтому существует такое δ > 0, что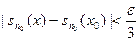 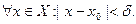Тогда получаем:

то есть функция s(x) непрерывна при х = х₀.

Теорема 40.3. Пусть функции u_n(x) непрерывны на отрезке [ a, b ] и ряд равно-мерно сходится на этом отрезке. Тогда ряд 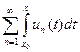тоже равномерно сходится на [ a, b ] и 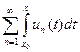(40.2)

(то есть в условиях теоремы ряд можно почленно интегрировать).

Доказательство.

По теореме 40.2 функция s(x) = непрерывна на [ a, b ] и, следовательно, интегрируема на нем, то есть интеграл, стоящий в левой части равенства (40.2), существует. Покажем, что ряд 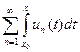равномерно сходится к функции

Обозначим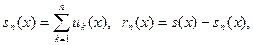

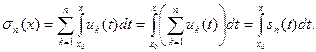Тогда для любого ε найдется такой номер N, что при n > N

Значит, ряд 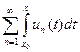равномерно сходится, и его сумма равна σ (х) = .

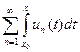Теорема доказана.

Теорема 40.4. Пусть функции u_n(x) непрерывно дифференцируемы на отрезке [ a, b ] и ряд, составленный из их производных:

(40.3)

равномерно сходится на [ a, b ]. Тогда, если ряд сходится хотя бы в одной точке 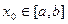, то он сходится равномерно на всем [ a, b ], его сумма s(x)= является непрерывно дифференцируемой функцией и

(ряд можно почленно дифференцировать).

Доказательство.

Определим функцию σ(х) как . По теореме 40.3 ряд (40.3) можно почленно интегрировать:

.

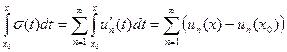Ряд, стоящий в правой части этого равенства, равномерно сходится на [ a, b ] по теореме 40.3. Но числовой ряд 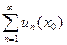по условию теоремы сходится, следовательно, равномерно сходится и ряд . Тогда Функция σ(t) является суммой равномерно сходящегося ряда непрерывных функций на [ a, b ] и поэтому сама непрерывна. Тогда функция непрерывно дифференцируема на [ a, b ], и 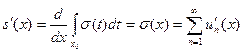, что и требовалось доказать.

Определение 41.1. Степенным рядом называется функциональный ряд вида

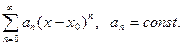(41.1)

Замечание. С помощью замены х – х₀ = t ряд (41.1) можно привести к виду 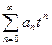, поэтому все свойства степенных рядов достаточно доказать для рядов вида

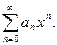(41.2)

Теорема 41.1 (1-я теорема Абеля). Если степенной ряд (41.2) сходится при х = х₀, то при любом x: | x| < |x₀| ряд (41.2) сходится абсолютно. Если же ряд (41.2) расходится при х = х₀, то он расходится при любом x: | x| > |x₀|.

Доказательство.

Если ряд сходится, то поэтому существует константа с > 0:

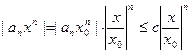. Следовательно, , а ряд 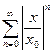при | x |<| x₀ | сходится, так как является суммой бесконечно убывающей геометрической прогрессии. Значит, ряд 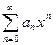при | x |<| x₀ | абсолютно сходится.

Если известно, что ряд (41.2) расходится при х = х₀, то он не может сходиться при | x| > |x₀|, так как из ранее доказанного при этом следовало бы, что он сходится и в точке х₀.

Таким образом, если найти наибольшее из чисел х₀ > 0 таких, что (41.2) сходится при х = х₀, то областью сходимости данного ряда, как следует из теоремы Абеля, будет интервал (- х₀, х₀), возможно, включающий одну или обе границы.

Определение 41.2. Число R ≥ 0 называется радиусом сходимости степенного ряда (41.2), если этот ряд сходится, а расходится. Интервал (-R, R) называется интервалом сходимости ряда (41.2).

Примеры.

1) Для исследования абсолютной сходимости ряда 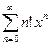применим признак Даламбера: 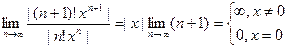. Следовательно, ряд сходится только при х = 0, и радиус его сходимости равен 0: R = 0.

2) Используя тот же признак Даламбера, можно показать, что ряд сходится при любом х, то есть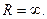

3) Для ряда 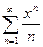по признаку Даламбера получим:

Следовательно, при –1 < x < 1 ряд сходится, при

x < -1 и x > 1 расходится. При х = 1 получаем гармонический ряд, который, как извест-но, расходится, а при х = -1 ряд 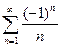сходится условно по признаку Лейбница. Таким образом, радиус сходимости рассматриваемого ряда R = 1, а интервал сходи-мости – [-1, 1).

Дата добавления: 2014-01-04