Однолистные функции. Обратные функции

Пусть 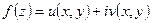– функция, аналитическая в некоторой области и, кроме того, принимающая в разных точках области разные значе­ния, т.е. такая, что , если 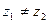. Такая функция на­зывается однолистной в области . Предположим ещё, что произ­водная 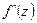этой функции непрерывна и не обращается в нуль внутри области (впоследствии мы увидим, что производная однолист­ной функции обладает этими свойствами). Рассмотрим теперь наряду с плоскостью комплексного переменного 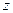плоскость комплексного переменного 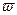и пусть 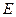– множество всех точек этой плоскости, соответствующих точкам области . Покажем, что это множество есть область, т.е. что оно, во-первых, состоит из одних лишь внутренних точек, и, во-вторых, – связное.

Действительно, пусть 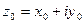– какая-либо точка области и 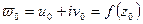- соответствующая ей точка множества 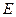. К уравнениям 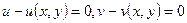можно применить теорему существования неявных функций, так как левые части этих уравнений обращаются в нуль при 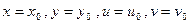, непрерывны по всем четырём переменным и имеют непрерывные част­ные производные, причём

якобиан не равен нулю. Поэтому существуют две непрерывные в некоторой окрестности точки функции , удовлетворяющие уравнениям 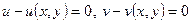и обращающиеся соответственно в и 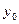в точке . Если взять окрестность точки достаточно малой, то точки будут сколь угодно близки к , т. е. будут лежать в области . 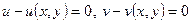А это значит, что некоторая окрестность точки целиком состоит из точек, соответствующих точкам области в силу уравнений , или, что то же, в силу уравнения , т.е. вся состоит из точек множества . Иными словами, всякая точка множества 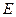является внутренней для этого множества. Чтобы доказать связность 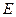, возьмём две любые точк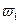и и 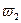этого множества и пусть и – соответствующие им точки области . Соединим и дугой Жордана, лежащей внутри . Если точка 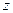будет описывать эту линию от к то точка опишет также линию Жордана от 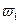к 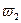. Послед­няя линия принадлежит к множеству 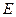по самому определению этого множества. Итак, 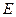действительно является областью.

В силу уравнения каждой точке 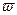области 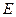соответ­ствует одна и только одна точка 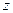области [только одна, потому что двум разным точкам 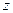в силу однолистности 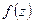должны соот­ветствовать разные точки 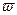]. Поэтому 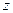можно рассматривать как функцию от 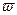, определённую в области 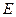. Эта функция – обозначим её через – является обратной по отношению к функции . Из того, что мы вывели выше, пользуясь теоремой о не­явных функциях, следует, что эта функция непрерывна [в самом деле, функции непрерывны относительно и ]. 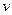Покажем, что функция – аналитическая в области .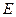

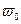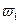Действительно, если точкам и области 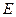соответствуют точки и области, то, переписывая отношение 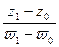в виде 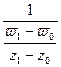и замечая, что, когда также стремится к , найдем:

,

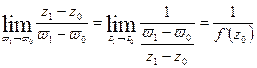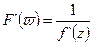т.е. производная от существует и равна , что и требовалось доказать.

Дата добавления: 2014-01-04