Волновое сопротивление

Комплексные действующие напряжения и ток запишем в таком виде:

(16.17)

По комплексным напряжению и току можно записать их оригиналы, то есть мгновенные значения этих величин:

(16.18)

Каждое слагаемое в уравнениях (16.18) есть бегущая волна составляющей напряжения (тока), движущаяся в направлении возрастания или убывания координаты x и затухающая по амплитуде в направлении движения.

Рассмотрим подробнее физический смысл составляющих напряжения и тока.

Если считать точку x фиксированной и рассматривать изменение первой составляющей напряжения в функции времени t, то она представляет собой синусоидальную функцию времени с постоянной амплитудой.

Если теперь считать фиксированным момент времени t и рассматривать изменение мгновенного значения составляющей напряжения вдоль линии (в зависимости от значений x), то имеем затухающую по амплитуде синусоидальную волну напряжения, причем амплитуда убывает по экспоненте от начала линии к ее концу.

Величина , входящая в показатель экспоненциальной функции 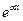называется, как уже было отмечено, коэффициентом затухания, а величина , равная изменению фазы сигнала (напряжения) на единицу длины линии, называется коэффициентом фазы.

В целом рассматриваемая составляющая напряжения называется прямой или падающей волной напряжения. Эта составляющая представляет собой бегущую волну напряжения, перемещающуюся с течением времени от начала линии к ее концу.

Соответственно, вторая составляющая напряжения 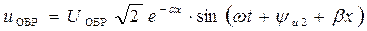называется обратной или отраженной бегущей волной; с течением времени эта волна перемещается от конца линии к ее началу.

Аналогично могут быть пояснены падающая и отраженная волны тока.

Убывание амплитуд волн вдоль линии обусловлено потерями в линии, то есть частичным расходом энергии волны на преодоление потерь на нагрев проводов и диэлектрика.

Падающие (или, соответственно, отраженные) волны напряжения и тока в совокупности и составляют единую электромагнитную бегущую волну.

Следует помнить, что физически в длинной линии существуют только результирующие напряжение u (t, x) и ток i (t, x), а их деление на прямые и обратные составляющие есть условный математический прием.

Отметим также, что коэффициент 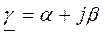является комплексным параметром линии, учитывающим как затухание волны (коэффициент затухания a), так и изменение ее фазы вдоль линии (коэффициент фазы b), то есть g характеризует распространение электромагнитной волны по линии.

6. Понятие о согласованной нагрузке, неискаженной передаче и передаче без потерь

Длинная линия, как правило, служит в качестве промежуточного передаточного звена (четырехполюсника) между источником электрической энергии и ее приемником (нагрузкой).

Если сопротивление приемника Z ₂ равно волновому сопротивлению линии

Z _{2 = 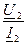=} Z _В, (16.19)

то коэффициент отражения K_u (1.26) равен нулю:

K_u = 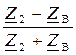= = 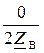0. (16.20)

и отраженная волна не возникает.

Нагрузка, при которой Z ₂ = Z _В и отсутствует отраженная волна, называется согласованной нагрузкой линии.

При согласованной нагрузке

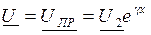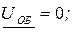; (16.21)

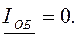(16.22)

Тогда для любой точки линии отношение комплексов U / I равно волновому сопротивлению Z _В:

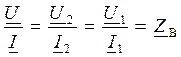. (16.23)

Режим работы источника питания линии не изменится, если линию разрезать в любом сечении и вместо отрезанной части включить волновое сопротивление Z _В.

В заключение укажем, что в режиме согласованной нагрузки (Z ₂ = Z _В) входное сопротивление линии равно ее волновому сопротивлению.

Пусть начальная фаза падающей волны напряжения (16.18) в конце линии равна нулю (y _u1 = 0), тогда

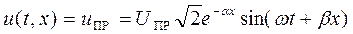. (16.24)

В этом случае начальная фаза падающей волны тока i _пр будет равна сдвигу по фазе q между напряжением и током:

, (16.25)

где угол q есть аргумент волнового сопротивления .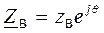

Отсчет x в последних выражениях для тока и напряжения ведется от конца линии.

Падающая электромагнитная волна, определяемая совокупностью падающих волн напряжения и тока (16.18), изображена на слайде.

Оценим КПД линии передачи.

Мощность, отдаваемая источником в линию

.

Мощность, передаваемая по линии к приемнику электрической энергии

.

С учетом формул (16.21) и (16.22) можем записать

(16.26)

и КПД линии передачи

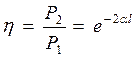. (16.27)

Таким образом, КПД нагруженной на согласованную нагрузку линии передачи энергии изменяется вдоль линии, уменьшаясь к ее концу.

В линиях связи любой передаваемый сигнал представляет собой совокупность (множество) гармоник различных частот.

Неискаженной передачей сигнала называется такая передача, при которой форма сигнала на входе и на выходе линии одинакова, то есть все ординаты кривой тока (или напряжения) в конце линии строго пропорциональны соответствующим ординатам кривой тока (напряжения) в начале линии.

Такая передача была бы возможна при условии, что коэффициент затухания a и коэффициент фазы b были бы одинаковы на всех частотах. В реальной линии неодинаковое затухание сигнала на различных частотах создает так называемые амплитудные искажения, а неодинаковая скорость распространения волн на различных частотах приводит к фазовым искажениям сигнала.

Для неискаженной передачи требуется выполнить два условия:

1) обеспечить независимость коэффициента a от частоты и 2) обеспечить пропорциональное частоте изменение коэффициента фазы b. При этом фазовая скорость v = w /b становится независимой от частоты w.

Эти условия обеспечиваются при соотношении параметров линии:

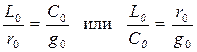. (16.28)

Линия, удовлетворяющая условию (16.26), называется линией без искажения.

Волновое сопротивление линии без искажений – действительное число (активное сопротивление), не зависящее от частоты

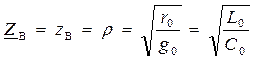. (16.29)

Фазовая скорость такой линии постоянна

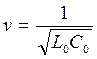. (16.30)

Отметим, что на практике выполнить условие (16.28) довольно сложно, так как в реальных линиях (особенно кабельных).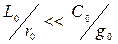

Наилучшим средством для выполнения соотношения является искусственное увеличение L₀ включением в линию индуктивных катушек или применением кабеля, проводящие жилы которого обмотаны тонкой лентой из ферромагнетика с высокой магнитной проницаемостью.

Условия отсутствия потерь в линии. Если принять равными нулю сопротивление проводов (r ₀ = 0) и проводимость утечки между проводами (g ₀ = 0), то такая линия может считаться линией без потерь. Реально к таким линиям можно с известным приближением отнести высокочастотные двухпроводные воздушные и кабельные линии.

Такая идеализация допускается для приближенной оценки характера процессов в линии, а расчетные соотношения существенно упрощаются.

Вторичные параметры линии можно записать так:

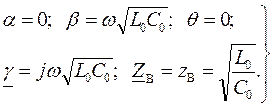(16.31)

Поскольку фазовая скорость постоянна

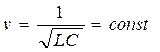, (16.32)

отсутствуют и фазовые искажения.

На основе записанных уравнений (16.18)-(16.30) и производится анализ всех режимов в линии без потерь.

Анализ распределения напряжений и токов вдоль линии при различных режимах можно производить как для мгновенных, так и для действующих их значений.

Уравнения мгновенных значений напряжения и тока при начальной фазе y _u2 = 0 (U ₂ = U ₂) и имеют вид (без вывода) [2]:

(16.33)

Кривые распределения тока и напряжения вдоль линии показаны на слайде.

Из графиков видно, что для каждого из этих моментов распределение напряжения и тока вдоль линии синусоидальное; рассматривая кривые одновременно, можно наблюдать волновой характер изменения u и i во времени.

Дата добавления: 2014-01-04