Бессрочный аннуитет

Аннуитет называется бессрочным (perpetuity), если денежные поступления продолжаются достаточно длительное время. Ма­тематически это означает, что 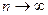. Характерным примером бессрочного аннуитета являются консоли - выпускаемые правительствами некоторых стран облигации, по которым произво­дят регулярные купонные выплаты, но которые не имеют фик­сированного срока. В западной практике к бессрочным относят­ся аннуитеты, рассчитанные на 50 и более лет. Бессрочный ан­нуитет также называют и вечной рентой.

В этом случае прямая задача (определение будущей стоимости аннуитета) не имеет смысла, однако обратная задача (определение приведенной стоимости аннуитета) имеет решение. Поток платежей в постоянном бессрочном аннуитете при одном денежном поступлении А за период, являющийся базовым для начисления процентов по ставке , представляет собой бесконечно убывающую геометрическую прогрессию с первым членом и знаменателем . Для бессрочного аннуитета постнумерандо, используя (7.16) при 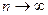, полу­чим:

(7.45)

где .

Соотно­шение (7.45) можно получить и из (7.17), вычисляя предел при 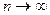. Формула (7.45) показывает, что поток даже с неограни­ченным числом платежей имеет все же конечную приведенную стоимость. С финансовой точки зрения это понятно, поскольку деньги, которые поступят через много лет, сейчас мало что сто­ят (а при высокой инфляции практически ничего не стоят). Эта же ситуация проявляется и при сравнении коэффициентов дисконтирования бессрочного аннуитета и аннуитетов с большим сроком. Рассмотрим значения 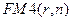при 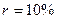в виде таблицы.

Дата добавления: 2014-01-04