
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Выражение матриц ориентации твердого тела через самолетные и корабельные углы
|
|
|
|
.
Ordm;. Физический смысл углов Эйлера
Ordm;. Схема ввода углов ориентации
Определение
.
Теорема доказана.
Углы 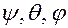 , введенные при построении матрицы ориентации в доказательстве теоремы Эйлера, называются углами Эйлера.
, введенные при построении матрицы ориентации в доказательстве теоремы Эйлера, называются углами Эйлера.
Знание углов Эйлера в любой момент времени 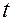 при движении твердого тела позволяет вычислить матрицу ориентации твердого тела на данном движении.
при движении твердого тела позволяет вычислить матрицу ориентации твердого тела на данном движении.
Доказательство теоремы Эйлера позволяет сформулировать простые правила и построить схему ввода углов Эйлера.
Правила и схему легко обобщить на случай ввода любых других трех независимых угловых величин, по которым может быть однозначно вычислена матрица ориентации.
Пусть в момент времени 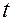 известны углы Эйлера
известны углы Эйлера 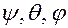 . Перенумеруем оси в любой декартовой прямоугольной системе координат.
. Перенумеруем оси в любой декартовой прямоугольной системе координат.
Будем называть 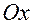 осью 1,
осью 1, 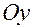 — осью 2,
— осью 2, 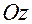 — осью 3.
— осью 3.
Соответственно, 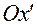 — это также ось с номером 1,
— это также ось с номером 1, 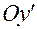 — ось с номером 2,
— ось с номером 2, 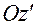 —ось с номером 3 в связанной системе.
—ось с номером 3 в связанной системе.
Обозначим  систему координат, совпадающую в момент времени
систему координат, совпадающую в момент времени 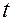 с абсолютной системой
с абсолютной системой 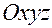 .
.
Покажем, как, зная углы 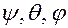 , с помощью трех последовательных поворотов системы
, с помощью трех последовательных поворотов системы  можно совместить ее со связанной системой
можно совместить ее со связанной системой 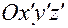 .
.
Процесс совмещения будем проводить в три этапа.
На первом этапе повернем систему  вокруг третьей оси, т.е. вокруг оси
вокруг третьей оси, т.е. вокруг оси  , так, чтобы ось
, так, чтобы ось  совпала с линией узлов. Это значит, что между новым положением оси
совпала с линией узлов. Это значит, что между новым положением оси  и старым образовался угол
и старым образовался угол 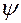 .
.
Новое положение системы  обозначим
обозначим 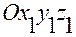 . Произведенное нами действие сформулируем в виде первого правила:
. Произведенное нами действие сформулируем в виде первого правила:
«Первый поворот совершается вокруг оси 3 на угол 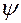 ».
».
Схематически действие по такому правилу обозначим:
 |
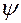
Цифра 3 внутри круга указывает номер оси, вокруг которой происходит поворот на угол 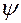 на первом этапе.
на первом этапе.
|
|
|
На втором этапе повернем систему 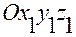 вокруг оси
вокруг оси  (т.е. вокруг оси 1) так, чтобы ось
(т.е. вокруг оси 1) так, чтобы ось  совпала с положением оси
совпала с положением оси 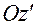 связанной системы.
связанной системы.
Поставленная цель достигается поворотом на угол 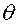 вокруг линии узлов
вокруг линии узлов  . Новое положение осей
. Новое положение осей 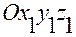 обозначим
обозначим  .
.
Описанное действие формулируется в виде второго
правила:
«Второй поворот совершается вокруг оси 1 на угол 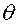 ».
».
Действие по правилу 2 схематически изобразим по аналогии с действием по правилу 1:
 |
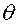
Цифра 1 внутри круга указывает номер оси, вокруг которой происходит поворот на угол 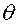 на данном этапе.
на данном этапе.
Поскольку действие по правилу 2 производится только после того, как сделан поворот на угол 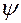 на первом этапе, то, объединяя последовательность двух поворотов в единую схему, получим:
на первом этапе, то, объединяя последовательность двух поворотов в единую схему, получим:
 |
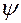
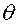
Здесь стрелка указывает на то, что поворот вокруг оси 1 на угол 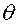 осуществляется после поворота вокруг оси 3 на угол
осуществляется после поворота вокруг оси 3 на угол 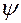 .
.
На третьем этапе систему  , полученную из
, полученную из 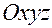 двумя первыми поворотами на углы
двумя первыми поворотами на углы 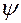 и
и 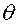 , повернем вокруг оси
, повернем вокруг оси 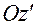 (оси 3) так, чтобы она совместилась полностью с окончательным положением осей
(оси 3) так, чтобы она совместилась полностью с окончательным положением осей 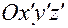 .
.
Совмещение осей будет достигнуто, если повернем систему  на угол
на угол 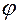 .
.
Из описанных действий следует, что система координат  , совпадающая в момент времени
, совпадающая в момент времени 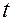 с абсолютной системой
с абсолютной системой 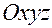 , может быть совмещена с угловым положением связанной системы
, может быть совмещена с угловым положением связанной системы 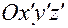 с помощью трех последовательных поворотов на конечные углы
с помощью трех последовательных поворотов на конечные углы 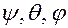 вокруг одной из координатных осей промежуточных систем координат.
вокруг одной из координатных осей промежуточных систем координат.
Каждая промежуточная система строится из предшествующей системы координат поворотом на один из перечисленных углов.
На последнем, третьем этапе действий необходимо
руководствоваться правилом:
«Третий поворот совершается вокруг оси 3 на угол 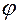 ».
».
Схематически этап 3 можно представить так:
|
|
|
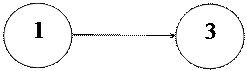 |
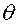
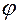
В расшифровке предложенная схема означает, что поворот координатных осей должен проводиться вокруг оси 3 на угол 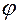 из положения, которое система достигла после поворота вокруг оси 1 на угол
из положения, которое система достигла после поворота вокруг оси 1 на угол 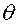 .
.
Объединяя схемы действий, описанных на каждом этапе процесса перевода системы  в положение связанной системы
в положение связанной системы 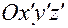 , задаваемое в момент времени
, задаваемое в момент времени 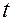 углами Эйлера
углами Эйлера 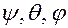 , приходим к следующей общей схеме такого перехода:
, приходим к следующей общей схеме такого перехода:
 |
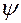
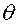
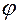
Она называется схемой ввода углов ориентации. В данном контексте она отражает схему ввода углов Эйлера.
Поясним физический смысл углов Эйлера. Рассмотрим их на примере движения волчка.
Наблюдения показывают, если пренебречь трением опоры волчка, то ось симметрии волчка совершает следующее движение.
Обозначим 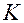 — конец орта оси симметрии, начало системы координат —
— конец орта оси симметрии, начало системы координат — 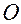 , а
, а  — проекцию точки
— проекцию точки 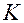 на плоскость
на плоскость 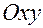 .
.
Точка  находится в плоскости
находится в плоскости 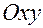 во все время движения, причем, если конструктивно волчок выполнен точно (т.е. является симметричным относительно оси вращения, и все его массы расположены симметрично), то точка
во все время движения, причем, если конструктивно волчок выполнен точно (т.е. является симметричным относительно оси вращения, и все его массы расположены симметрично), то точка  движется по окружности.
движется по окружности.
Радиус 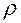 окружности равен
окружности равен 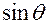 , где
, где 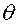 — угол между осями
— угол между осями 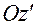 и
и 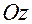 (см. рис. 3.4.5).
(см. рис. 3.4.5).
Об этом движении говорят, что волчок совершает
прецессию.
Точнее говоря, прецессией волчка называют вращение вокруг вертикальной оси 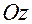 плоскости, проходящей через эту ось и ось симметрии волчка.
плоскости, проходящей через эту ось и ось симметрии волчка.
Если симметрия волчка конструктивно нарушена, то точка  одновременно с прецессией, т.е. вращением вокруг полюса
одновременно с прецессией, т.е. вращением вокруг полюса 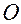 в плоскости
в плоскости 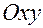 , совершает колебательное движение между двумя окружностями радиуса
, совершает колебательное движение между двумя окружностями радиуса 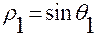 и
и 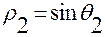 (см. рис. 3.4.6).
(см. рис. 3.4.6).

Рис. 3.4.5 Рис.3.4.6
Здесь 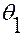 — минимальное значение угла
— минимальное значение угла 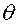 , а
, а  — максимальное. Иначе говоря,
— максимальное. Иначе говоря,  — колебательная функция. Такое движение волчка называется его нутационным колебанием.
— колебательная функция. Такое движение волчка называется его нутационным колебанием.
Все остальные материальные точки волчка, расположенные вне оси симметрии, по отношению к этой оси совершают круговые движения по углу 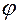 . Их движения называется собственным вращением волчка.
. Их движения называется собственным вращением волчка.
Таков физический смысл углов Эйлера. Отсюда они получили название:
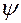 – угол прецессии,
– угол прецессии, 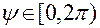 ;
;
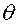 – угол нутации,
– угол нутации, 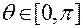 ;
;
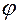 – угол собственного вращения,
– угол собственного вращения, 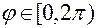 .
.
|
|
|
4º. Построение углов Эйлера
по заданной матрице ориентации
Дадим ответ на следующий вопрос:
если матрица 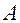 задана, то можно ли определить углы Эйлера по ее элементам?
задана, то можно ли определить углы Эйлера по ее элементам?
Матрица 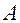 имеет вид:
имеет вид:
Из третьего столбца матрицы 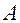 находим
находим
 ,
, 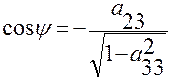 ,
,  .
.
Из третьей строки матрицы 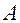 получим
получим
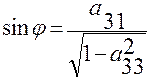 ,
,  .
.
Эти соотношения справедливы только в том случае, когда 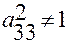 , т.е. при
, т.е. при  и
и 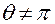 .
.
При 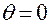 и
и  матрица
матрица 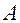 , соответственно, принимает вид:
, соответственно, принимает вид:
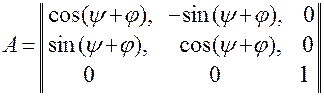 ;
;
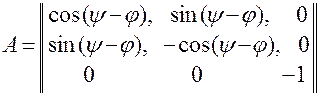 .
.
Из данных выражений матрицы 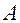 можно вычислить по первому столбцу при
можно вычислить по первому столбцу при 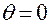 только угол
только угол 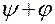 и угол
и угол  при
при  .
.
Эта особенность принципиальная, ибо при 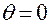 и при
и при  плоскости
плоскости 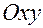 и
и 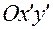 совпадают, и понятие линии узлов отсутствует.
совпадают, и понятие линии узлов отсутствует.
В такой ситуации в качестве линии узлов можно взять любую прямую, находящуюся в плоскости 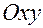 .
.
И если по общему правилу задать углы 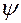 и
и 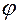 относительно линии узлов, то по этим углам однозначно будут вычисляться элементы матрицы
относительно линии узлов, то по этим углам однозначно будут вычисляться элементы матрицы 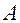 , поскольку положение осей
, поскольку положение осей 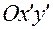 по отношению к
по отношению к 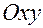 при
при 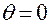 определяется суммой углов
определяется суммой углов 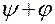 , а при
, а при  — разностью углов
— разностью углов  .
.
Однако обратная задача — задача определения значений углов Эйлера по элементам матрицы 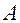 — не будет иметь решения, поскольку углы
— не будет иметь решения, поскольку углы 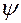 и
и 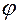 не могут быть вычислены при
не могут быть вычислены при 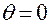 и
и  .
.
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 1384; Нарушение авторских прав?; Мы поможем в написании вашей работы!