Обернена теорема. Якщо проекція похилої l перпендикулярна до прямої р, то ця похила також перпендикулярна до прямої р

Властивість точок бісекторної площини. Кожна точка бісек­торної площини рівновіддалена від граней двогранного кута. Обернене твердження: якщо точка рівновіддалена від граней двогранного кута, то вона належить його бісекторній площині.

При перетині двох площин утворюються чотири двогранних кути. Якщо лінійний кут одного з цих двогранних кутів прямий, то ці площини називаються взаємно перпендикулярними.

Теорема 2 (ознака перпендикулярності площин). Якщо пряма а, перпендикулярна до площини α, належить площині β, то площини α і β взаємно перпендикулярні (рис. 3).

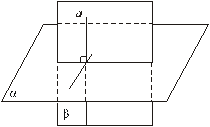
Рис. 3

Перпендикулярною проекцією точки А на площину α називається основа перпендикуляра, опущеного з точки А на площину α.

Проекцією фігури на площину α називається множина точок площини α, що є проекціями всіх точок цієї фігури. Проекцією прямої на площину є також пряма (або, в частинному випадку, точка). Якщо пряма а перетинає площину α в точці А, то проекція прямої також проходить через точку А.

Якщо пряма а паралельна площині α, то її проекція буде паралельною прямій а.

Властивості, проектування

1. Якщо прямі а і b паралельні, то їхні проекції паралельні або, в окремих випадках, являють собою одну пряму або дві точки.

2. Якщо точка С поділяє відрізок АВ у відношенні m: n (рис. 4), то при проектуванні точка 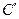поділяє відрізок у тому самому відношенні, тобто

Рис. 4

Теорема 3 (про три перпендикуляри). Якщо похила l перпен­дикулярна до деякої прямої р площини α, то її проекція також перпендикулярна до прямої р (рис. 5).

Рис. 55

Нехай висота піраміди ABCD, опущена з вершини D, проходить через точку перетину висот Δ АВС (ортоцентр трикутника). Можна довести, що протилежні ребра такої піраміди попарно перпендикулярні і будь-яка інша її висота також проходить через ортоцентр протилежної грані (рис. 6).

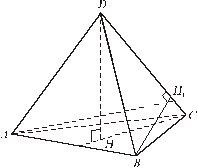
Рис. 6

Кутом між прямою l і площиною α називається кут між прямою α і її проекцією на площину α (кут φ на рис. 5).

Можна довести, що коли всі бічні ребра піраміди ABCD нахилені до площини основи АВС під однаковими кутами, то висота DO проходить через центр O описаної біля Δ АВС кола.

Рис. 7

15.9. Многогранники. Площі поверхонь.
Об’єм многогранників

Якщо у двох паралельних площинах α і β містяться рівні між собою п -кутники, відповідні сторони яких попарно паралельні, а відповідні вершини сполучено відрізками, то утворений у такий спосіб многогранник називається призмою (рис. 8).

Многокутники, що лежать у площинах α і β, називаються основами призми. Чотирикутники АВВ ₁ А ₁, ВВ ₁ С ₁ С та інші називаються бічнимигранями призми і являють собою паралелограми; відрізки AA ₁, BB ₁ та інші називаються бічними ребрами призми. Усі бічні ребра призми рівні між собою і паралельні. Висотою призми називається відстань між площинами α і β, тобто довжина перпендикуляра, опущеного з будь-якої точки площини α на площину β.

Рис. 8

Площа бічної поверхні призми дорівнює добутку периметра її перпендикулярного перерізу на довжину бічного ребра.

Об’єм призми дорівнює добутку площі основи на висоту приз­ми або площі перпендикулярного перерізу на довжину бічного ребра:

Прямою називається призма, бічні ребра якої перпендикулярні до площини основи.

Правильною називається пряма призма, в основі якої лежить правильний многокутник.

Частинними випадками призми є прямокутний паралелепіпед — пряма призма, в основі якої лежить прямокутник, і куб — правильна призма, в основі якої лежить квадрат. Об’єм прямокутного паралелепіпеда дорівнює добутку довжин трьох ребер, що виходять з однієї вершини.

Нехай на площині α лежить опуклий многокутник А ₁ A ₂ A ₃… А_n, а точка S не належить площини α. Сполучивши точку S із вершинами многокутника, дістанемо многогранник, що називається
п - кутною пірамідою (рис. 9). Многокутник А ₁ A ₂ A ₃... А_n називається основою піраміди. Висотою піраміди називається відрізок перпендикуляра, опущеного з вершини S на площину підстави.

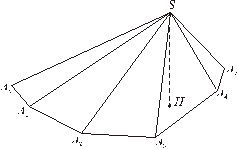
Рис. 9

Правильною називається піраміда, в основі якої лежить правильний многокутник, а висота проходить через центр кола, описаного навколо основи.

Дата добавления: 2014-01-04