Критерии и свойства оптимальных стратегий

Тема 3. Лекция 9. Антагонистические игры.

Теорема 1. Пусть V — цена игры, H(P⁰,Q⁰) — функция выигрыша, S_A и S_B— множество смешанных стратегий А и В.

1. Для того чтобы стратегия P⁰ игрока А была оптимальной необходимо и достаточно, чтобы выполнялось неравенство

H(P⁰,Q) ≥ V (1.)

для любого QS_B, т.е. выбор игроком А оптимальной стратегии P⁰ гарантирует ему выигрыш H(P⁰,Q⁰), не меньше цены игры V, при любой стратеги Q игрока В.

2. Для того чтобы стратегия Q⁰ игрока В была оптимальной необходимо и достаточно, чтобы выполнялось неравенство

H(P,Q⁰) ≤ V (2.)

для любого РS_А, т.е. выбор игроком В одной из своих оптимальных стратегий Q⁰

гарантирует ему проигрыш не больший цены V, при любой стратеги Р игрока А.

Теорема 1 остается в силе, если в ее формулировке множества смешанных стратегий S_А и S_В заменить на множество 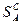и . А именно имеет место

Теорема 2. Пусть V — цена игры, H(P,Q) — функция выигрыша, 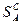={А₁,…,Аm} и {В₁,…,Вn}— множество чистых стратегий соответственно игроков А и В.

1) Для того чтобы стратегия Р⁰ игрока А была оптимальной необходимо и достаточно, чтобы

Н(Р, В_j)≥ V, j =1, …, n. (10.)

2) Для того чтобы стратегия Q⁰ игрока В была оптимальной необходимо и достаточно, чтобы

Н(А_i, Q⁰) ≤ V, i =1, …, m. (11.)

В теоремах 1. и 2 критерии оптимальности стратегий сформулированы в предположении, что априори известна цена игры V.

В следующей теореме в терминах смешанных стратегий дается критерий решения игры (т.е. совокупности цены игры V и пары оптимальных стратегий Р⁰ и Q⁰ соответственно игроков А и В).

Теорема 3. Для того чтобы V было ценой игры, а Р⁰ и Q⁰ – оптимальными стратегиями соответственно игроков А и В, другими словами, для того чтобы { Р⁰,Q⁰, V } было решением игры, необходимо и достаточно выполнение двойного неравенства

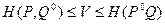(.14)

Для любых Р и Q .

Аналогично теореме 2 в формулировке 3 множества смешанных стратегий и можно заменить соответственно на множество чистых стратегий 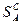= {A₁,…,A_m}и 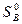= {В₁,…,В_n}, т.е. справедлива

Теорема 4. Для того чтобы V была ценой игры, а Р⁰ и Q⁰ – оптимальными стратегиями соответственно игроков А и В, необходимо и достаточно выполнение двойного неравенства:

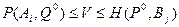, i =1, …, m, j =1, …, n. (19)

Пример 1.

Установить цену игры V и оптимальность смешанных стратегий Р ° = (0,4; 0,6) и Q ° = (0; 0; 0,6; 0,4) для игры с платежной матрицей 2x4

Bj Ai	B1	B2	B3	B4
A1
A2

Пример2. Предположим, что в условиях примера 1 мы априори знаем, что V=0,625 –цена игры, а Р⁰=(3/8,5/8) и Q⁰(1/4,0,3/4) – оптимальные стратегии. Покажем, как можно воспользоваться достаточной частью теоремы 4 для установления цены игры и оптимальности стратегий игроков.

Расположим указанные в примере 1 значения функции выигрыша , i =1, 2; 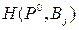, j =1, 2,3, в неубывающем порядке:

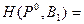0,625; 0,625; 0,625; 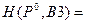0,625; 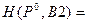0,656.

Из этой последовательности очевидно выполнение , i =1, 2, j =1, 2,3.

Тогда по достаточной части теоремы 4 значение V=0,625 является ценой игр, а Р⁰=(3/8,5/8) и Q⁰(1/4,0,3/4) – оптимальными стратегиями.

Сформулируем еще один критерий решения игры в терминах седловых точек функции выигрыша.

Теорема 5. Для того чтобы V было оценкой игры, а Р⁰, Q⁰ – оптимальные стратегии соответственно игроков А и В необходимо и достаточно, чтобы (Р⁰, Q⁰) была седловой точкой функции выигрыша Н (Р, Q) и

Н(Р⁰, Q⁰)= V (20)

Так как теоремы 3, 4, 5 представляют необходимые и достаточные условия решения игры, то они эквивалентны.

Теперь рассмотрим некоторые важные свойства оптимальных стратегий.

Пусть Р⁰=()- оптимальная смешанная стратегия игрока А. В общем случае, некоторые из вероятностей могут быть равными нулю. Если 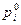=0, где i- одно из чисел 1,…,m, то в оптимальной смешанной стратегии Р⁰=() чистая стратегия А_i не участвует и потому называется пассивной.

Чистые стратегии А_i , входящие в оптимальную стратегию Р⁰ с положительной вероятностью, называется активной.

Таким же образом определяются активные стратегии игрока В. Понятно, что оптимальная чистая стратегия является активной.

Следующая теорема об активных стратегиях играет существенную роль в решении игр.

Теорема 6. (об активных стратегиях) Пусть V – цена игры, Р⁰=() и Q⁰=(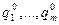) – оптимальные стратегии соответственно игроков А и В. Тогда

1) Для любой активной стратегии игрока А выполняется равенство

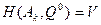(21)

2) Для любой активной стратегии игрока B выполняется равенство

(22)

Теорема об активных стратегиях означает, что если один из игроков действует по своей оптимальной смешанной стратегии, то выигрыш не изменится и останется равным цене игры V, при условии, что другой игрок придерживается любой своей чистой активной стратегии.

Заметим, что активная стратегия A_k игрока А, для которой по теореме 6, хотя и выполняется равенство H(A_k,Q⁰) = V, может не быть оптимальной по причине невыполнения равенства 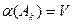. Аналогичное замечание имеет место и для активных стратегий В_l игрока В.

Теорему 6 эквивалентным образом сформулировать в терминах так называемых «смесей чистых активных стратегий». Определим это понятие.

Пусть Р⁰=() – смешанная оптимальная стратегия игрока А, I – произвольное непустое подмножество множества {>0}= {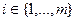}: Ai – активная стратегия} номеров активных стратегий игрока А относительно данной смешанной оптимальной стратегии Р⁰.

Смешанная стратегия Р⁰=() такая, что

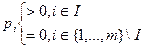(33)

Называется смесью чистых активных стратегий игрока А.

Если, в частности {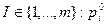>0}, то смесь Р⁰=() активных стратегий называется полной. Если же множество I состоит из единственного номера к, то смесь активных стратегий превращается в активную стратегию А_к

Аналогичным образом определяются смеси чистых активных стратегий игрока В.

Теорема 7. (о смесях активных стратегий) Пусть V – цена игры, Р⁰=() и Q⁰=(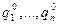) – оптимальные смешанные стратегии. Тогда

1) Для любой смеси активных стратегий Р=(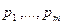) игрока А справедливо равенство

H(Р,Q⁰) = V (34)

2) Для любой смеси активных стратегий Q=() игрока В справедливо равенство

Н(Р⁰, Q) = V (35)

Теорема о смесях активных стратегий говорит о том, что если один из игроков придерживается своей оптимальной смешанной стратегии, то выигрыш остается неизменным и равным цене игры V, если только другой игрок применяет смеси своих стратегий в произвольных пропорциях.

Пример 2.10.5. Рассмотрим игру в примере 2 с оптимальными стратегиями Р⁰ (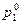= 3/8, = 5/8) и Q⁰ (=1/4, = 0, 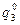= 3/4) соответственно игроков А и В.

Множество номеров чистых стратегий В, которые входят в оптимальную стратегию Q⁰ с положительными вероятностями, J= {1, 3}.

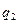Рассмотрим смешанную стратегию Q⁰ = (=3/5, = 0, 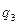= 2/5) игрока В. Поскольку

То смешанная стратегия Q является смесью активных стратегий В₁и В₃ игрока В в пропорциях соответственно 3/5 и 2/5. Тогда, по теореме 7 о смесях активных стратегий,

H(Р,Q⁰) = V = 0,625.

В этом можно убедиться и прямым подсчетом:

Наконец, отметим, что смесь Q не является оптимальной стратегией игрока В, так как показатель неэффективности стратегии Q отличается от цены игры: > V.

В самом деле:

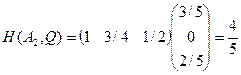
Тогда

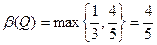> 0,625 = V.

Дата добавления: 2014-01-04