Устойчивость линейных САУ. Понятие устойчивости

В простейшем случае понятие устойчивости системы связано со способностью её возвращаться (с определённой точностью) в состояние равновесия после исчезновения внешних сил, которые вывели её из этого состояния.

Наглядно устойчивость равновесий представлена на рисунке:

Положение равновесия шара хар-ся точкой . В случае I при при бесконечном отклонении шара от положительного равновесия, он стремится снова возвратиться к положительному равновесию .I – устойчивое положение равновесия; II – неустойчивое; III – безразличное.

Дадим строгое определение устойчивости (дано русским ученым А.М. Ляпуновым в 1892).

Пусть движение САУ описывается дифференциальным ур-ем:

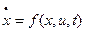или (1)

где xi – вещественная переменная, характеризующая состояние системы упрощения; xi – известные функции переменных 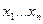и времени t, удовлетворяющее условиям (существования и единственности) решения ДУ; 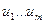- управляющие воздействия, подаваемые на систему .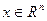

Если для всех U(t)=0, то система называется свободной.

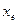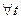Определение 1. Состояние свободной системы называется состоянием (положением) равновесия, если для (2)

Очевидно, что если для 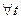, то система, находящаяся в 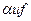состоянии, в нем и останется (скорости нет => не сдвинется в отсутствие внешних сил).

Состояние равновесия называют также невозмущенным движением.

Пусть система под воздействием внешних сил отклонилась от невозмущенного движения, а затем внешние силы при t=t0 сняты. Движение системы с момента времени t0 зависит от начального отклонения 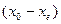, от положения равновесия 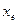. Отклонение 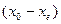наз-ся возмущением.

Т.о. 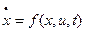- Ур-е возмущенного дв-я

- Ур-е невозмущенного дв-я

Определение 2. (Устойчивость по Ляпунову)

Состоянием равновесия 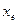(невозмущенное движение 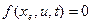) наз-ся устойчивым всмысле Ляпунова, если для такое, что для возмущения , удовлетворяющее условию будет выполняться условие 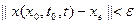для .

Критерии устойчивости делятся на 2 группы:

1) алгебраические критерии (Гурвица, Рауса)

2) частотные критерии (Найквиста, Михайлова)

Критерий устойчивости Гурвица (без д-ва):

Дана линейная стационарная система, характ. полином к-ой имеет вид:

.

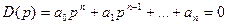Составим по нему матрицу Гурвица размера nxn следующего вида:

Порядок составления:

1) По главной диагонали выписываются по порядку к-ты a1..an

2) строка дополняется таким образом, чтобы слева направо индексы возрастали, и чтобы строки с четными и нечетными индексами чередовались. Вместо к-тов с индексами, меньшими 0 и большими n, пишут нули.

Определителями Гурвица , где i=1,…,n называются главные диагональные миноры м-цы Гурвица.

; ; …

Теорема. Для того, чтобы линейная стационарная система была асимптотически устойчива, Н и Д, чтобы при a0>0 все определители Гурвица были положительны (при а0<0 – наоборот). Система находится в состоянии устойчивости, если

и , где i=1,2,…,n-1

Но т.к. 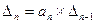, то имеют место 2 случая:

1. - апериодическая граница устойчивости (один из корней хар-го Ур-я =0)

2.- колебательная граница устойчивости (2 комплексно-сопряженных корня хар-го Ур-я, находящихся на мнимой оси)

Частные случаи.

1. Система 1го порядка:

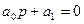
Н=а1 => условие устойчивости: ,

1. Система 2го порядка: :

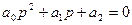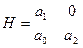; Условие устойчивости: ;; ;

Вывод: для систем 1 и 2 порядка Н иД условием устойчивости является положительность всех к-тов хар-го Ур-я.

1. Система 3го порядка:

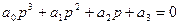
; Условие устойчивости: , ;

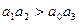Из 2х последних Ур-й => . Т.о. для устойчивости системы 3 порядка кроме положительности всех к-тов требуется еще, чтобы 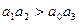, т.е. чтобы произведение средних к-тов хар-го Ур-я было больше произведения крайних.

Дата добавления: 2014-01-04