Основные термины

Т

дх¹

= а

• +

(д^г1 д²1 д²А

ду² дг²

(2.54)

Уравнение (2.54) необходимо дополнить условиями однозначности в виде:

1. Геометрических условий - задают форму и размеры рассматриваемого тела

'о> *Ь ^2> ••• > '«•

2. Физических условий - коэффициент теплопроводности стенки тела Х_ст - сопз1, теплоемкость тела С = сопз*, плотность р = сопзх,

3. Начальных условий - температура рассматриваемого тела в начальный момент времени при т = 0 распределена равномерно, т. е. Го ~ сопзг.

4. Граничных условий III рода - задают закон теплообмена между поверхностью тела и окружающей средой в виде следующего уравнения:

= --р('«*-'«.)> (2-55)

(Ы\ где — - температурный градиент по поверхности тела; а - коэффициент теплоотдачи

\^д")пов.

между поверхностью тела и окружающей средой, Вт/(м²-°С); 1_пов, 1_0а - температуры

поверхности тела и окружающей среды, °С.

Решение дифференциального уравнения теплопроводности (2.54) совместно с

условиями однозначности дает уравнение температурного поля следующего вида:

I = Да,Х_ст,а,г,х,у,г, 1₀,1_0С, 1₀,1_}, 1₂,..., 1_п). (2.56)

Из зависимости (2.56) видно, что температура зависит от большого числа переменных и постоянных параметров. При анализе уравнения (2.56) оказывается, что переменные можно сгруппировать в безразмерные комплексы:

— = В1 - критерий Био (характеризует неравномерность температурного поля);

"ст ах

= Ро - критерий Фурье (характеризует нестационарность процессов);

хД - безразмерная координата; 1-г_Пг 9

'о.с.

1<\~1пг 9<\

безразмерная температура;

()/()о - безразмерное количество теплоты ((?_т - количество теплоты, переданное телу или телом за время т, ^о - начальная внутренняя энергия тела).

Если ввести безразмерные комплексы в исходные зависимости (2.53), то получим

О. (2.57)

-^ = /₂(Го,В0

Решение данных уравнений представляет собой довольно сложную математическую задачу. Подробные решения трех простейших задач нестационарной теплопроводности для неограниченной пластины, цилиндра бесконечной длины и шара приводятся в специальных курсах по теплообмену [3, 4]. В п. 2.2.2.2. настоящего пособия приведем готовые расчетные зависимости для случая охлаждения неограниченной пластины. Изучив метод решения задачи для пластины, можно понять принцип решения задач и для тел другой геометрической конфигурации.

2.2.2.2. Охлаждение неограниченной пластины при нестационарном

режиме

Рассмотрим охлаждение плоскопараллельной пластины толщиной 23 (характерный размер 1 = 3), Размеры пластины в направлении осей У и 2 бесконечно велики (рис. 2.14). С обеих сторон пластина омывается жидкостью с температурой (_ох_, причем коэффициент теплоотдачи а для обеих поверхностей имеет одинаковое и постоянное значение.

В начальный момент времени при т = 0 пластина имеет во всех своих точках постоянную температуру /о⁼ сопз*, поэтому избыточная температура во - (о- 4& будет также постоянной для всех точек тела. Кроме того, заданы коэффициент теплопроводности Х_ст, плотность тела/? и его теплоемкость С, величины которых полагаются постоянными.

Г,°С

дв_ дг

Так как пластина безгранична как по высоте, так и по ширине, то дифференциальное уравнение принимает вид

а-

(2.58)

д²в дх²

Начальное условие при г = 0 в=во. Граничное условие при х = ±3

,, + <

(2.59)

(дв)

"ст

где в„ - избыточная температура поверхности пластины.

Рис. 2.14. Неограниченная пластина

Для аналитического решения уравнения (2.58) совместно с условиями однозначности используют метод разделения переменных. Решение ищется в виде произведения двух функций, из которых одна является функцией только г, а другая - только х:

в = в(х_>т) = <р(т)-ф). (2.60)

выражения

(2.60)

После подстановки дифференциальное уравнение (2.58) получим

(2.61)

^ф) = аЩ$-ф) или <р'(т)-ф) = аУ(х)-ф).
дт дх²

В последнем уравнении переменные легко разделяются, и его можно записать следующим образом:

<р(т) у/(х) Решение дифференциального уравнения (2.62) может быть представлено в виде

(2.62)

*~*х,г

в

С08

М1

2 8Ш Щ

в₀,₌1#+8Ш#С08# V /

,-^Ро

(2.63)

где щ - промежуточная переменная, которая находится из уравнения

В1

(2.64)

Из анализа уравнения (2.64) следует, что при каждом значении числа Ш существует бесконечное множество решений. Наиболее просто уравнение (2.64) можно решить графическим способом.

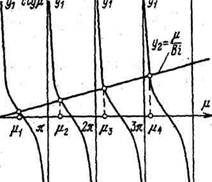
Обозначим левую часть уравнения (2.64) через у\— &§ц, а правую - через уг-ц I Вг. Пересечение котангенсоиды у\ с прямой уг дает нам значение корней характеристического уравнения, т. е. //, (см. рис. 2.15).

Из рис. 2.15 следует, что мы имеем бесконечное множество значений величины //,-, причем каждое последующее значение больше предыдущего/*; <ц₂ </и₃ <... <//,• <....

Таким образом, уравнение температурного поля (2.63) удовлетворяет исходному уравнению теплопроводности (2.58) при любом значении /*,-.

С одной стороны, из физических соображений О ясно, что температура не может иметь множество значений в определенной точке в данный момент времени. С другой стороны, не ясно, какое значение щ нужно выбрать.

Известно, что если частные решения линейного дифференциального уравнения сложить, то полученная сумма также будет решением этого дифференциального уравнения. Следовательно, Рис. 2.15. Графики функций^ и ^2 значения щ нужно использовать в совокупности, поэтому в формуле (2.63) присутствует знак суммы. В инженерных расчетах можно ограничиться первыми тремя-четырьмя значениями //,-.

Важно отметить, что каждому значению числа Вг отвечает овоя совокупность корней уравнения (2.64). Первые четыре корня уравнения (2.64) приведены в табл. 2.1 для различных значений числа Вг.

При Вг -* да прямая уг = /и I Вг совпадает с осью абсцисс, и корни уравнения будут

равны: ^=|;//₂ =-*;•••;//_й=(2и-1)|.

При В1 —> 0 прямая уг = ц I Вг совпадает с осью ординат, и тангенс угла наклона прямой стремится к бесконечности, при этом корни уравнения (2.64) будут равны: щ = 0; ц₂ = к;цз = 2я;...;/*„ = («- 1)я.

Таблица 2.1 Значения щ для неограниченной пластины

Вг	И1	Ц2	Мз	М4	Вг	А/	И2	Из	М4
	0,0000	3,1416	6,2832	9,4248	1,0	0,8603	3,4256	6,4373	9,5293
0,001	0,0316	3,1419	6,2833	9,4249	1,5	0,9882	3,5422	6,5097	9,5801
0,002	0,0447	3,1422	6,2835	9,4250	2,0	1,0769	3,6436	6,5783	9,6296
0,004	0,0632	3,1429	6,2838	9,4252	3,0	1,1925	3,8088	6,7040	9,7240
0,006	0,0774	3,1435	6,2841	9,4254	4,0	1,2646	3,9352	6,8140	9,8119
0,008	0,0893	3,1441	6,2845	9,4256	5,0	1,3138	4,0336	6,9096	9,8928
0,01	0,0998	3,1448	6,2848	9,4258	6,0	1,3496	4,1116	6,9924	9,9667
0,02	0,1410	3,1479	6,2864	9,4269	7,0	1,3766	4,1746	7,0640	10,0339
0,04	0,1987	3,1543	6,2895	9,4290	8,0	1,3978	4,2264	7,1263	10,0949
0,06	0,2425	3,1606	6,2927	9,4311	9,0	1,4149	4,2694	7,1806	10,1502
0,08	0,2791	3,1668	6,2959	9,4333	10,0	1,4289	4,3058	7,2281	10,2003
0,1	0,3111	3,1731	6,2991	9,4354	15,0	1,4729	4,4255	7,3959	10,3898
0,2	0,4328	3,2039	6,3148	9,4459	20,0	1,4961	4,4915	7,4954	10,5117
0,3	0,5218	3,2341	6,3305	9,4565	30,0	1,5202	4,5615	7,6057	10,6543
0,4	0,5932	3,2636	6,3461	9,4670	40,0	1,5325	4,5979	7,6647	10,7334
0,5	0,6533	3,2923	6,3616	9,4775	50,0	1,5400	4,6202	7,7012	10,7832

Окончание таблицы 2.1

ы	Ш	М2	Мз	Н4	Вг	М1	И2	Из	М4
0,6	0,7051	3,2304	6,3770	9,4879	60,0	1,5451	4,6353	7,7259	10,8172
0,7	0,7506	3,3477	6,3923	9,4983	80,0	1,5514	4,6543	7,7573	1 10,8606
0,8	0,7910	3,3744	6,4074	9,5087	100,0	1,5552	4,6658	7,7764	10,8871
0,9	0,8274	3,4003	6,4224	9,5190		1,5708	4,7124	7,8540	10,9956

В результате методика решения задачи теплопроводности при нестационарном режиме сводится к следующему. Сначала вычисляют значения критериев Ш и Ро, затем по табл. 2.1 определяют значения //,- и по формуле (2.63) рассчитывают отношение 0 = в/ во, из которого определяют искомую температуру I.

2.2.2.3. Частные случаи распределения температурного поля внутри

неограниченной пластины

Рассмотрим частные неограниченной пластины.

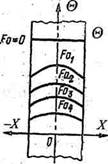
1. Очень большие значения числа Ш. Если Щ —» оо, то температура поверхности пластины сразу становится равной температуре окружающей среды, в которую помещена пластина (см. рис. 2.16 а). В этом случае при заданных физических параметрах и толщине пластины коэффициент теплоотдачи а — юв, т. е. имеет место большая интенсивность отвода теплоты от поверхности, поэтому процесс охлаждения определяется главным образом физическими свойствами и размерами тела.

2. Очень малые значения числа Щ (ВН < 0,1). Малые значения числа Вг могут иметь место при малых размерах толщины пластины, при больших значениях коэффициента теплопроводности X и малых значениях коэффициента теплоотдачи а. При малых числах Вг температура на поверхности пластины незначительно отличается от температуры на оси. Это указывает на то, что температура по толщине пластины распределяется равномерно, и кривая температур остается почти параллельной оси X для любого момента времени (см. рис. 2.16 б). В рассматриваемом случае процесс нагрева и охлаждения тела определяется интенсивностью теплоотдачи на поверхности пластины. Иначе говоря, процесс выравнивания температуры в пластине происходит существенно интенсивнее, чем отвод теплоты с поверхности.

случаи распределения температурного поля внутри

0 =1

Ра=0		\0
\!
		/V,
		%
		щ
		Гц
-X		■
	ч

в =1

X

40

Рис. 2.16. Распределение температуры при охлаждении неограниченной пластины в

условиях: _а_5/-+со, б-5/<0,1,в-0,1 < Ш < 100, для всех случаев Ро] <Ро₂<Ро₃<Ро₄.

3. Число Вг находится в пределах 0,1 < Ш < 100. В рассматриваемом случае есть функция Ш, т. е. зависит от толщины пластины. Температурные кривые для любого момента времени будут выглядеть, как показано на рис. 2.16 в. В этом случае интенсивность процесса охлаждения определяется как внутренним, так и внешним термическим сопротивлением.

Для облегчения инженерных расчетов построены графические зависимости вида

^пов. _ '■пов. *о.с _ ^в0 к~*о.с	А	ей ах \^лст *)	= Мт,Го)
в 1 -1 "ц '■ц ^1о.с г ^в0 'о ^_ ^1о.с	а1 ах \^лст * )	= Гг(т,Го),
	шшо) ■

(2.65)

(2.66)

(2.67)

В формулах (2.65) - (2.67): /_лоа - температура поверхности пластины; 1_Ц - температура центральной плоскости пластины; (Э_х - количество теплоты, переданной в окружающую среду за время т.

Эти зависимости приводятся в специальной литературе [1-3] в виде графиков или таблиц.

Термическое сопротивление стенки, тепловая проводимость стенки. >,, Нестационарный процесс теплопроводности. Критерии В1 и Ро.

Безразмерная координата, безразмерная температура, безразмерное количество теплоты.

Неограниченная пластина.

Дата добавления: 2014-01-04