Обработка многократных измерений постоянных величин

Правила записи и округления результатов измерений

Точность результатов измерений и последующих вычислений при обработке данных должна быть согласована с необходимой точностью результатов измерений. Погрешность результатов измерений следует выражать не более чем двумя значащими цифрами. Две значащие цифры следует давать в двух случаях:

- при проведении высокоточных наблюдений;

- при погрешности, выраженной числом с цифрой старшего разряда £ 3, например D = 22.

При обработке результатов измерений следует пользоваться правилами приближенных вычислений, а округление выполнять по следующим правилам:

1. Округлять результат измерения следует так, чтобы он оканчивался цифрой того же порядка, что и погрешность. Если значение результата измерения оканчивается нулями, то ноль отбрасывается до того разряда, который соответствует разряду погрешности.

Пример: погрешность D = ± 0,0005 м.

После вычислений получены результаты измерения:

Х₁ = 9,84236672 @ 9,8424; Х₂ = 1,260002 @ 1,2600

Правильная запись:

Х₁ = (9,8424 ± 0,0005) м; Х₂ = (1,2600 ± 0,0005) м.

2. Если первая из заменяемых нулем или отбрасываемых цифр (слева направо) меньше 5, то остающиеся цифры не изменяются.

Пример: D = 0,06; Х = 2,3641 @ 2,36.

3. Если первая из заменяемых нулем или отбрасываемых цифр равна 5, а за ней не следует никаких цифр или нулей, то округление производят до ближайшего четного числа, т.е. четную последнюю оставленную цифру или ноль оставляют без изменений, нечетную увеличивают на единицу.

Пример: D = ± 0,25

Х₁ = 1,385 @ 1,38;

Х₂ = 1,355 @ 1,36.

4. Если первая из заменяемых нулем или отбрасываемых цифр больше или равна 5, но за ней следует отличная от нуля цифра, то последнюю оставленную цифру увеличивают на единицу.

Пример: D = ± 12

Х₁ = 236,51 @ 237.

Типичные ошибки записи результата измерения представлены в табл. 6.

Таблица 6. Примеры записи результата

Правильно	Неправильно	Ошибка
1,2 ± 0,2	1,244 ± 0,2	Лишние цифры в значении результата
1,24 ± 0,03	1,2438 ± 0,0325	Лишние цифры в значении погрешности
1,244 ± 0,014	1,244 ± 0,01	Грубое округление погрешности
1,24 ± 0,03	1,24 ± 10^-2	Множитель 10^n должен быть общим

Многократным измерением называется измерение, результатом которого является совокупность возможных значений однократных результатов измерений y₁(х),..., y_m (х), где m ³ 2. Эту совокупность представим в форме вектора-столбца (x) = (y₁(х),..., y_m (х))^Т. Множеству возможных векторов соответствует случайный вектор многократных измерений 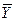(x) = (Y₁(x),…, Y_m(x))^T, где m. — объем многократных измерений.

Таким образом, измеряемая величина х, объем многократных измерений m. для конкретного СИ (совокупности СИ) в рабочих условиях измерения определяют случайный вектор многократных измерений 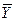(x). Пару структурных элементов (х, m) называют планом измерения для получения вектора многократных измерений.

Разумеется, вектор многократных измерений содержит больше информации об измеряемой величине х, чем результат однократного измерения. Поэтому его следует использовать для получения оценки дисперсии и более точной оценки измеряемой величины х, т. е. для получения оценок количественных значений величин. В общем случае искомую оценку Z количественного значения величины х можно представить в виде некоторой функции от составляющих вектора многократных измерений

Z(x) = f(Y₁(x),…, Y_m(x)) (1.19)

Как функция случайных аргументов оценка Z является случайной величиной. Вид функциональной зависимости выбирается таким, чтобы удовлетворялись два важных в прикладном отношении требования: во-первых, математическое ожидание оценки Z(x) совпадало бы с истинным значением оцениваемой величины и, во-вторых, дисперсия оценки (обозначим ее D_z) была бы минимальной.

Измерительные задачи, имеющие целью получение оценок количественных значений величин на основе вектора многократных измерений, будем называть измерительными задачами первого типа. Эти задачи решаются с использованием шкалы интервалов (метрической шкалы). При х - const план измерения такой задачи имеет вид (х, m).

Рассмотрим отношение, обеспечивающее единство измерений [Назаров]:

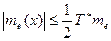(1.20)

На основе только этого отношения множество СИ можно разбить на два класса эквивалентности:

- класс СИ, формирующих результаты измерений, систематическая погрешность которых удовлетворяет отношению (1.20);

- класс СИ, формирующих результаты измерений, систематическая погрешность которых не удовлетворяет отношению (1.20).

Очевидно, что по величине т_е(х) СИ, принадлежащие первому классу, являются в качественном отношении предпочтительнее СИ, принадлежащих второму классу.

Пусть имеется некоторое СИ, принадлежность которого к классу эквивалентности по величине т_е(х) неизвестна. Оценка принадлежности СИ к классу эквивалентности выполняется с использованием решающей функции следующего вида:

s(u) = 0 – при u £ u₀ – принимается первый класс СИ;

s(u) = 1 – при u > u₀ – принимается второй класс СИ, (1.21)

где u₀ - параметр решающей функции, и — аргумент решающей функции.

Преобразование, реализуемое выражением (1.21), является алгоритмической шкалой порядка с двумя шкальными значениями.

Рассмотрим величину, которую можно взять в качестве аргумента решающей функции. Структуру однократного результата измерения можно представить в двух формах

Y(х) = т_у(х) + 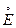= х + т_е(х) +,

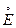где m_y(x)=M[Y(x)] — математическое ожидание случайной величины Y(x).

Из этого равенства следует

m_у(х) =х+т_е(х)

или

т_е(х) = т_у(х) – х (1.22)

Очевидно, что в качестве аргумента решающей функции нужно использовать оценку систематической погрешности. На основе выражения (1.22) ее можно сформировать следующим образом: вместо неизвестного значения величины х использовать ее действительное значение x_q, а вместо неизвестного значения математического ожидания т_у(х) - его оценку.

Возьмем в качестве оценки величины т_у(х) результат измерения Y(х). Тогда получим

М_е(х) =Y(x) - x_q = x + m_e(х) + 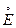- x_{q ½ x - xq<<me(x) ½} » т_е(х) + .

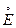Недостатком этой оценки является большой разброс ее возможных значений, обусловленный центрированной случайной составляющей 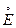с дисперсией D_e. Использование такой оценки в решающей функции (1.21) привело бы к большим вероятностям ошибок при оценке принадлежности СИ к классам эквивалентности.

Уменьшить эти вероятности ошибок можно, если в качестве оценки математического ожидания т_y(х) использовать оценку, полученную на основе вектора многократных измерений 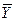(x), т. е. оценку

Z(x) = f(Y₁(x),…, Y_m(x))

Если ее выбрать такой, чтобы выполнялись условия:

1. M[Z(x)]=m_y(x),

2. M[Z²(x)]=D_z<D_e,

то такая оценка будет иметь следующую структуру:

Z(х) = т_у(х) + 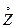= х + т_е(х) + ,

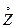а оценка систематической погрешности будет равна

М_е(х) = Z(х) – x_q = х + т_е(х) + 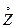- x_q = т_е(х) + 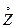= m_e(х) + ,

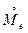где 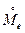= 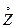- центрированная случайная составляющая оценки М_е(х).

Дисперсия составляющей 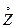зависит от объема многократных измерений, т. е. D_z(m). С увеличением объема m она уменьшается так, что D_z (m) = 0. Следовательно, за счет выбора значения m можно обеспечить малый разброс возможных значений оценки М_е(х) и, как следствие, малые вероятности ошибок оценки принадлежности к классу эквивалентности.

Рассмотренная измерительная задача обладает следующими особенностями: во-первых, как и измерительная задача первого типа, использует вектор многократных измерений 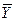(x) и, во-вторых, оценка принадлежности к классу эквивалентности реализуется на основе решающей функции (1.21) с параметром u ₀. Формирование случайного вектора многократных измерений производится на основе плана измерения (x_q, m), а оценка принадлежности к классу эквивалентности - с использованием алгоритмической шкалы порядка, характеризующейся параметром и₀.

Измерительные задачи, имеющие целью получение оценки принадлежности объекта измерения к классу эквивалентности на основе вектора многократных измерений и решающей функции называются измерительными задачами второго типа. Эти задачи решаются с использованием экспериментальной шкалы интервалов и алгоритмической шкалы порядка (наименований). План измерения такой задачи имеет вид (x, m, u₀).

Алгоритмы обработки многократных измерений представлены более подробно в [Назаров].

Глава 6. Применение информационной теории для оценки результатов и погрешностей измерений.

Дата добавления: 2014-01-04