
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекция 11. Линейная квадратичная задача (ЛК-задача) оптимального управления
Линейная квадратичная задача (ЛК-задача) оптимального управления
Проблема, возникающая при реализации рассмотренных выше методов выбора расположения полюсов заключается в том, что они (методы) полностью игнорируют допустимую величину управления. Поэтому проектировщику нужно осуществлять множество итераций, чтобы добиться желаемого результата. Задача остается прежней: как можно быстрее вернуть систему из возмущенного начального состояния в нулевое состояние при ограничении максимального значения управления.
Рассмотрим альтернативный метод расположения полюсов, получивший название линейной квадратичной (ЛК) задачи оптимального управления или задачи линейного квадратичного регулятора (ЛКР).
Пусть ОУ описывается уравнением состояния
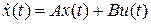 , (1)
, (1)
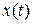 есть n - вектор,
есть n - вектор, 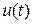 есть r -вектор. Начальное состояние есть
есть r -вектор. Начальное состояние есть 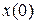 . Мы предполагаем, что все переменные состояния измеримы и ставим задачу найти закон управления с обратной связью по состоянию (другими словами, найти коэффициент обратной связи по состоянию
. Мы предполагаем, что все переменные состояния измеримы и ставим задачу найти закон управления с обратной связью по состоянию (другими словами, найти коэффициент обратной связи по состоянию 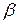 )
)
 , (2)
, (2)
который обеспечивает желаемые свойства для проектируемой замкнутой системы, другими словами, желаемое расположение полюсов замкнутой системы. С учетом этого закона уравнение состояния замкнутой системы можно записать как
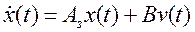 , (3)
, (3)
где  является матрицей замкнутой системы и
является матрицей замкнутой системы и  задающее воздействие. Заметим, что матрица выхода C не используется в данном законе управления.
задающее воздействие. Заметим, что матрица выхода C не используется в данном законе управления.
Условия, в которых биологическая жизнь может существовать, являются очень узкими. В ходе эволюции изменение температуры воздуха на несколько градусов приводило к исчезновению целых популяций. Источники энергии живого организма, такие как клетки, весьма ограничены по своей мощности. Поэтому многие биологические организмы развивались так, чтобы они постепенно становились оптимальными в смысле использования минимальных усилий, требуемых для поддержания своего гомеостазиса или равновесия. С очень малыми затратами на выделение соответствующих химических продуктов через мембрану клетки, клетка может поддерживать разность потенциалов вдоль мембраны, необходимую для ее (клетки) жизнедеятельности и нормального функционирования.
Так как многие встречающиеся в живой природе системы являются оптимальными, то разумно спроектировать искусственные (рукотворные) регуляторы так, чтобы они были оптимальными. Чтобы спроектировать оптимальную обратную связь по состоянию, мы, прежде всего, должны определить скалярный показатель качества (другое название, целевая функция, функция стоимости) в виде функционала
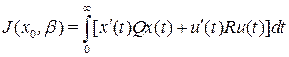 . (4)
. (4)
Мы предполагаем, что задающее воздействие равно нулю,  =0, т.к. нас интересует здесь свойство внутренней устойчивости замкнутой системы, т.е. мы рассматриваем задачу регулирования. Подставляя (2)
=0, т.к. нас интересует здесь свойство внутренней устойчивости замкнутой системы, т.е. мы рассматриваем задачу регулирования. Подставляя (2)  при
при  =0 в (4), получаем
=0 в (4), получаем
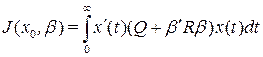 . (5)
. (5)
Цель оптимального проектирования состоит в том, чтобы найти такой коэффициент обратной связи по состоянию 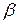 , который минимизирует показатель качества J.
, который минимизирует показатель качества J.
Показатель качества мы интерпретируем как функцию энергии, так что, делая его малым, мы добиваемся малого расхода всей энергии замкнутой системы. Заметим, что как  x (t), так и
x (t), так и 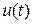 входят с весовыми коэффициентами в подынтегральное выражение для J, поэтому, если J мало, то ни x (t), ни
входят с весовыми коэффициентами в подынтегральное выражение для J, поэтому, если J мало, то ни x (t), ни 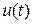 не могут быть большими. Заметим, что если показатель J минимизирован, то он, разумеется, равен конечной величине, и так как этот показатель есть интеграл в бесконечных пределах времени от x (t), то это означает, что x (t) стремится к нулю, когда t стремится к бесконечности. Это обстоятельство, в свою очередь, гарантирует устойчивость замкнутой системе.
не могут быть большими. Заметим, что если показатель J минимизирован, то он, разумеется, равен конечной величине, и так как этот показатель есть интеграл в бесконечных пределах времени от x (t), то это означает, что x (t) стремится к нулю, когда t стремится к бесконечности. Это обстоятельство, в свою очередь, гарантирует устойчивость замкнутой системе.
Две матрицы Q (матрица n  n) и матрица R (матрица r
n) и матрица R (матрица r  r) выбираются проектировщиком системы. Это параметры настройки, аналогичные коэффициентам настройки ПИД-регулятора. В зависимости от того, как выбраны эти параметры замкнутая система будет демонстрировать различную реакцию на ненулевое начальное состояние. Вообще говоря, выбор большого значения Q при сохранении того же самого значения J приводит к меньшим отклонениям x (t) (речь идет о скалярном случае). Это означает, что чем больше значения Q, тем дальше удалены влево от мнимой оси полюсы замкнутой системы (собственные значения матрицы замкнутой системы
r) выбираются проектировщиком системы. Это параметры настройки, аналогичные коэффициентам настройки ПИД-регулятора. В зависимости от того, как выбраны эти параметры замкнутая система будет демонстрировать различную реакцию на ненулевое начальное состояние. Вообще говоря, выбор большого значения Q при сохранении того же самого значения J приводит к меньшим отклонениям x (t) (речь идет о скалярном случае). Это означает, что чем больше значения Q, тем дальше удалены влево от мнимой оси полюсы замкнутой системы (собственные значения матрицы замкнутой системы  ), так что состояние быстрее стремится к нулю. Напротив выбор значения R большим означает, что управляющее воздействие
), так что состояние быстрее стремится к нулю. Напротив выбор значения R большим означает, что управляющее воздействие 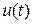 должно быть малым при том же самом значении J. С другой стороны, чем больше R, тем меньшие управляющие усилия используются, следовательно, полюсы в общем случае располагаются близко от мнимой оси, в результате получаются большие отклонении состояния x (t).
должно быть малым при том же самом значении J. С другой стороны, чем больше R, тем меньшие управляющие усилия используются, следовательно, полюсы в общем случае располагаются близко от мнимой оси, в результате получаются большие отклонении состояния x (t).
Нужно выбирать матрицу Q положительно полуопределенной и матрицу R положительно определенной. Это означает, что скалярная величина, квадратичная форма  будет всегда положительной или равной нулю в каждый момент времени t при любой функции x (t), и скалярная величина, квадратичная форма
будет всегда положительной или равной нулю в каждый момент времени t при любой функции x (t), и скалярная величина, квадратичная форма 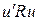 будет всегда положительной в каждый момент времени t при любой функции
будет всегда положительной в каждый момент времени t при любой функции 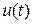 . Это гарантирует, что критерий J четко определен. В рамках собственных значений для выполнения вышеопределенных условий собственные значения Q должны быть неотрицательными, в то время как собственные значения R должны быть положительными. Если обе матрицы выбраны диагональными (обычный случай), то это означает, что все элементы R должны быть положительными, в то время как элементы матрицы Q должны быть положительными, однако допускается наличие некоторых нулевых коэффициентов на ее главной диагонали. Заметим, что положительно определенная матрица R является обратимой.
. Это гарантирует, что критерий J четко определен. В рамках собственных значений для выполнения вышеопределенных условий собственные значения Q должны быть неотрицательными, в то время как собственные значения R должны быть положительными. Если обе матрицы выбраны диагональными (обычный случай), то это означает, что все элементы R должны быть положительными, в то время как элементы матрицы Q должны быть положительными, однако допускается наличие некоторых нулевых коэффициентов на ее главной диагонали. Заметим, что положительно определенная матрица R является обратимой.
Так как объект управления линейный и показатель качества квадратичный, то задача определения коэффициента обратной связи по состоянию 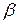 , минимизирующего J, называется задачей линейного квадратичного регулятора (ЛКР). Слово регулятор относится к тому факту, что назначение этой обратной связи возвращать (регулировать) исходное ненулевое состояние к нулю. Эта задача отличается от задачи слежения, когда целью управления является заставить управляемую величину следовать за предписанным задающим (желаемым) воздействием.
, минимизирующего J, называется задачей линейного квадратичного регулятора (ЛКР). Слово регулятор относится к тому факту, что назначение этой обратной связи возвращать (регулировать) исходное ненулевое состояние к нулю. Эта задача отличается от задачи слежения, когда целью управления является заставить управляемую величину следовать за предписанным задающим (желаемым) воздействием.
Чтобы найти оптимальный коэффициент обратной связи по состоянию, мы поступим следующим образом. Предположим, что существует симметричная постоянная матрица P такая, что
 . (6)
. (6)
Тогда подставляя это выражение в (5) 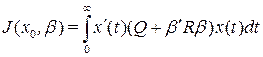 , получаем
, получаем
 . (7)
. (7)
Здесь мы предполагаем, что замкнутая система является устойчивой, так что x (t) стремится к нулю при t 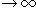 . Уравнение (7) означает, что J не зависит от
. Уравнение (7) означает, что J не зависит от 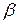 . Т.е.
. Т.е. 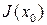 постоянная величина, которая зависит только от вспомогательной матрицы P и начальных условий.
постоянная величина, которая зависит только от вспомогательной матрицы P и начальных условий.
Теперь мы найдем 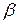 так, чтобы предположение, касающееся выражения (6), имело место. С этой целью продифференцируем левую часть (6)
так, чтобы предположение, касающееся выражения (6), имело место. С этой целью продифференцируем левую часть (6) 
 .
.
Учитывая уравнение замкнутой системы (3) 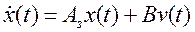 и что v (t)=0, получаем
и что v (t)=0, получаем
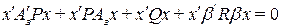
или находим уравнение
 ,
,
эквивалентное (6).
Теперь заметим, что последнее уравнение имеет место для всех x (t). Поэтому выражение в скобках должно быть тождественно равно нулю. Следовательно, с учетом  ,
,
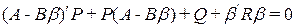
или
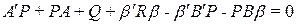 .
.
Это матричное квадратичное уравнение. Точно также как для скалярного случая его можно дополнить до полного квадрата
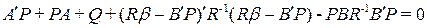 .
.
Теперь пусть мы выбрали
 . (8)
. (8)
Тогда получаем уравнение
 , (9)
, (9)
которое не содержит 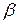 .
.
Полученный результат чрезвычайно важен в современной теории. Уравнение (9) известно как алгебраическое уравнение Рикатти (АУР). Оно названо по имени графа Рикатти, итальянского ученого, который жил в 19-м столетии и использовал подобные уравнения при изучении тепловых потоков.

Это есть матричное квадратное уравнение, которое может быть разрешено относительно вспомогательной матрицы P при заданных A,B,Q,R. Затем находим оптимальный коэффициент обратной связи по состоянию 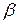 , определяемый (8). Минимальное значение критерия качества, получаемое при использовании оптимального коэффициента, определяется (7) и зависит только от начальных условий. Это означает, что затраты (стоимость), связанные с использованием коэффициента (7) могут быть вычислены по начальным условиям еще до того, как управление будет приложено к объекту.
, определяемый (8). Минимальное значение критерия качества, получаемое при использовании оптимального коэффициента, определяется (7) и зависит только от начальных условий. Это означает, что затраты (стоимость), связанные с использованием коэффициента (7) могут быть вычислены по начальным условиям еще до того, как управление будет приложено к объекту.
Процедура, связанная с определением коэффициента обратной связи по состоянию для ЛКР регулятора, включает в себя:
· Выбор параметров проектирования матриц Q и R;
· Решение алгебраического уравнения Рикатти относительно симметричной P;
· Вычисление оптимального коэффициента обратной связи по состоянию, используя  .
.
Имеется очень хорошая процедура численного решения уравнения АУР. Рутина MATLAB, с помощью которой осуществляется это решение, называется lqr (A,B,Q,R).
Процедура проектирования ЛКР гарантирует получение обратной связи по состоянию, которая стабилизирует систему при выполнении следующих требований:
ЛКР теорема. Пусть объект (A,B) управляем. Пусть R положительно определенная и Q положительно полуопределенная матрицы. Тогда замкнутая система ( ) является асимптотически устойчивой.
) является асимптотически устойчивой.
Пример 1. Пусть объектом управления служит двойной интегратор, описываемый уравнениями в переменных состояния
 .
.
Так как объект имеет один вход, то критерий качества запишем в виде
 .
.
Легко убедиться, что пара (A,B) управляема. Выберем  и приступим к решению алгебраического уравнения Рикатти. Пусть
и приступим к решению алгебраического уравнения Рикатти. Пусть 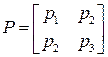 , где мы явно используем факт, что матрица
, где мы явно используем факт, что матрица 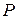 является симметричной. Подставляя
является симметричной. Подставляя 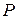 , Q, A, R =
, Q, A, R = в (9)
в (9)  и учитывая, что для положительной полуопределености
и учитывая, что для положительной полуопределености 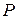 все ее диагональные элементы должны быть неотрицательны, находим решение
все ее диагональные элементы должны быть неотрицательны, находим решение
 .
.
Оптимальная замкнутая система определяется уравнением
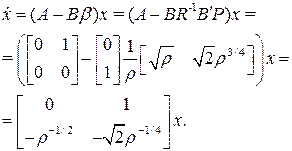
Полюсы замкнутой системы являются корнями характеристического уравнения 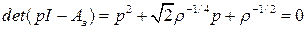 . Это уравнение имеет форму стандартного характеристическог уравнения системы второго порядка
. Это уравнение имеет форму стандартного характеристическог уравнения системы второго порядка  при
при 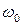 =
=  и
и  =1/
=1/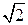 . Относительный коэффициент затухания оптимальной замкнутой системы 1/
. Относительный коэффициент затухания оптимальной замкнутой системы 1/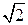 часто трактуется как лучший компромисс между малым перерегулированием и достаточно высоким быстродействием, и он не зависит от
часто трактуется как лучший компромисс между малым перерегулированием и достаточно высоким быстродействием, и он не зависит от  . При фиксированном относительном коэффициенте затухания, чем больше собственная частота
. При фиксированном относительном коэффициенте затухания, чем больше собственная частота 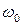 , тем больше быстродействие системы (вспомним, что время наступления первого пика переходной характеристики обратно пропорционально
, тем больше быстродействие системы (вспомним, что время наступления первого пика переходной характеристики обратно пропорционально 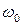 ). Таким образом, мы видим, что если
). Таким образом, мы видим, что если  уменьшается, то быстродействие системы увеличивается. Т.к. малое значение
уменьшается, то быстродействие системы увеличивается. Т.к. малое значение  влечет за собой малый штраф, накладываемый на управление, и отсюда приводит к большим значениям управляющего воздействия, то рассмотренный пример дает хорошую интерпретацию роли квадратичного веса
влечет за собой малый штраф, накладываемый на управление, и отсюда приводит к большим значениям управляющего воздействия, то рассмотренный пример дает хорошую интерпретацию роли квадратичного веса 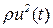 в критерии качества J.
в критерии качества J.
Пример 2. Давайте рассмотрим объект, описываемый уравнениями


и критерий качества
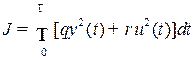 ,
,
где 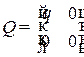 и
и  . Здесь q и
. Здесь q и 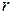 положительные коэффициенты. Легко убедиться, что объект является полностью управляемым. Положительно полуопределенное решение уравнения Рикатти и векторный коэффициент обратной связи по состоянию при использовании обозначений
положительные коэффициенты. Легко убедиться, что объект является полностью управляемым. Положительно полуопределенное решение уравнения Рикатти и векторный коэффициент обратной связи по состоянию при использовании обозначений 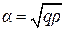 и
и  имеют вид
имеют вид
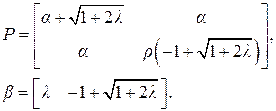
Заметим, что последний зависит только от отношения 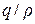 , а не от q и
, а не от q и 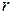 в отдельности. Рис. ниже показывает изменение во времени управления и управляемой величины как реакции на начальное состояние
в отдельности. Рис. ниже показывает изменение во времени управления и управляемой величины как реакции на начальное состояние 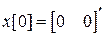 для различных
для различных 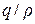 . Чем больше отношение
. Чем больше отношение 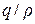 , тем быстрее управляемая величина стремится к нулю, однако ценой более «сильного» управления.
, тем быстрее управляемая величина стремится к нулю, однако ценой более «сильного» управления. 

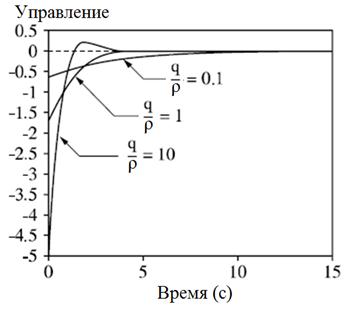
Кроме учета допустимого управления, ЛКР обладает еще одним важным достоинством: оно придает высокую робастность замкнутой системе управления. Так для системы с одним выходом и одним входом при любых Q и R запас устойчивости по фазе оказывается не менее 60 градусов, а запас устойчивости по модулю не менее 2.
|
|
Дата добавления: 2014-01-04; Просмотров: 2958; Нарушение авторских прав?; Мы поможем в написании вашей работы!