Елементи теорії гвинтової пари

Співвідношення між осьовою силою, що діє на болт, та моментом сил, прикла–деним до гайки при її загвинчуванні. У болтовому з'єднан­ні взаємна нерухомість деталей забезпечується відповідною затяж­кою болта. При загвинчуванні гайки (рис 11.6) осьова сила F₀ у стержні болта зростає; при цьому збільшується і момент Т, що при­кладається до гайки.

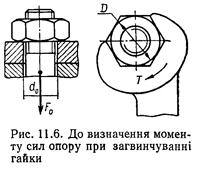
Цей момент дорівнює сумі моментів сил тертя в різьбі та на торці гайки:

Т = Т_SP+T_ST. (2)

Момент сил тертя в різьбі при загвинчуванні гайки визначається за формулою

T_SP = 0,5F₀d₂tg(ψ + ρ). (З)

Опорна торцева площина гайки має форму кільця, обмеженого ді­аметрами d₀ і D (рис. 11.6). Тому момент сил тертя на такій площині при рівномірному розподілі тиску можна записати у вигляді

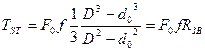(4)

У формули (3) та (4) входять такі величини: d₂ – середній діаметр різьби болта; ψ – кут підйому витків різьби; ρ = arctg 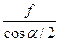– зведений кут тертя в різьбі; α – кут про­філю витків різьби; f – коефіцієнт тертя ковзання; R_3B – зведений радіус сил тертя на кільцевій площині торця гайки, що визнача­ється за виразом

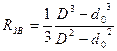(5)

Підставляючи (3) і (4) у вираз (2), дістаємо

T = F₀(0,5d₂tg(ψ + ρ) + f R_ЗВ). (6)

Наближена геометрична подібність метричних різьб різних діаметрів дає змогу для орієнтовних розрахунків використовувати простіші співвідношення, що добуті для середніх значень розрахункових пара­метрів. Для метричної різьби з нормальним кроком можна взяти: ψ ≈ 2° 3О'; d₂ ≈ 0,9d; R_зв ≈ 0,7d і f = 0,15 (для різьби без покрит­тя). Тоді момент, що прикладається до гайки при її загвинчуванні, на основі виразу (6) може бути визначений за формулою

T = 0,2F₀d. (7)

Якщо припустити, що довжина ручного гайкового ключа дорів­нює в середньому 14d, то, прирівнюючи момент на ключі, що створю­ється силою Q руки, і момент Т, дістанемо співвідношення між осьо­вою силою F₀, яка діє на болт, та силою Q, прикладеною до ключа:

F₀ ≈ 70Q. (8)

Таким чином, за допомогою кріпильних різьб можна мати виграш у силі приблизно в 70 разів (при f = 0,1 – у 100 разів).

Вираз (6) беруть за основу при створенні спеціальних динамо­метричних ключів, що використовуються для контрольованої затяж­ки різьбових з'єднань.

Розподіл осьової сили, що діє на болт, на витках різьби. Осьова сила F на болті передається через витки його різьби на гайку (рис. 11.7). При цьому кожний виток різьби навантажується відпо­відно силами F_l, F₂,..., F_z. Сума всіх сил становить загальну осьову силу F на стержні болта:

F = F₁ + F₂ + ··· + F_z (9)

За умови рівномірного розподілу сил на кожний виток

F₁ = F₂ =... =F_z = F/z, (10)

де z – число витків різьби в гайці.

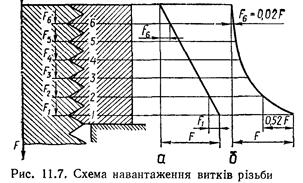
У такому разі епюру осьових сил у різних перерізах стержня болта зображають прямою лі­нією (рис. 11.7, а). Тут наван­таження від витка до витка рів­номірно зменшується на F/z.

У дійсності витки різьби у звичайних гайках навантажую­ться нерівномірно. Однією із причин нерівномірного розподі­лу навантаження на витках різь­би є те, що стержень болта розтягується (крок його витків збільшу­ється), а гайка стискається (крок її витків зменшується).

Теоретичне розв'язування задачі про розподіл навантаження на витках різьби було зроблене М. Є. Жуковським у 1902 р. і в подаль­ших експериментальних дослідженнях неодноразово підтверджене. Так, у стандартній гайці з шістьма витками перший зі сторони опор­ної площини гайки виток різьби сприймає близько 52 % осьової си­ли F, а останній, шостий – тільки 2 % (рис. 11.7, б).

Рівномірність розподілу осьової сили на витках різьби можна поліпшити використанням спеціальних гайок. Одним із способів досягнення цієї мети є застосування конструкцій гайок, в яких ді­лянки матеріалу з різьбою деформуються аналогічно з деформацією стержня гвинта. На рис. 11.8, а, б показані конструкції гайки, в яких матеріал, що знаходиться в області різьби, розтягується так, як і ма­теріал стержня гвинта. В наведених прикладах збільшення податли­вості гайок у зоні найбільш навантажених витків також сприяє ви­рівнюванню навантаження витків різьби.

Спеціальні гайки в основному застосовують у з'єднаннях, що зна­ходяться під дією динамічних навантажень. Руйнування різьбових деталей з'єднання в цьому випадку має втомний характер і відбува­ється в місцях найбільшої концентрації напружень або в зоні най­більш навантаженого витка різьби. За дослідними даними викорис­тання спеціальних гайок може підвищити границю витривалості різьбових з'єднань на 20–ЗО %.

Дата добавления: 2014-01-05