Представление периодических функций времени в частотной области. Ряд Фурье

Основные параметры помех

Помехи можно представить и описать как во временной, так и в частотных областях. Обычно не так важно точное описание формы помехи, как ее точные параметры, от которых зависит ее мешающее воздействие.

Параметры помех могут быть определены для периодических помех:

частота f и амплитуда x _max;

Для непериодической помехи важнейшие параметры следующие:

скорость изменения Δ x /Δ t;

Δ t − интервал времени в течении которого Δ x /Δ t = max максимальное значение помехи Δ x.

Для взаимосвязанного представления этих величин с точки зрения электромагнитной совместимости используют при периодических помехах амплитудный спектр, а для импульсных спектр амплитудной плотности. Оба представления позволяют применительно к помехе:

- оценить воздействие помехи на узкополосную систему;

- рассчитать воздействие помехи на конкретное устройство;

- выбрать параметры средств подавления помех (фильтров);

- определить граничные области, например, максимального возможного или допустимого излучения помех или характеризовать границы помехоустойчивости;

- определить нормы электромагнитной совместимости устройств.

Важнейший параметр помехи при непериодических процессах – спектр амплитудной плотности, который может быть измерен экспериментально и сопоставлен со спектром импульсов трапецеидальной, прямоугольной или треугольной форм.

Синусоидальные или косинусоидальные помехи (гармоничес­кие процессы) могут быть представлены как во временной, так и в частотной областях непосредственно (рисунок 2.2). В частотной области помеха характеризуется угловой частотой ω и частотой колебаний .

Рисунок 2.2 - Представление синусоидальной помехи во временной и

частотной областях

Несинусоидальные периодические функции — например, пи­лообразной или прямоугольной формы импульсы напряжения или тока выпрямителей, которые в некоторых случаях возможно описать аналитически, — могут быть представлены в частотной области опосредованно, а именно как бесконечная сумма сину­соидальных и косинусоидальных колебаний, т. е. рядом Фурье. Например, можно представить себе несимметричное напряже­ние прямоугольной формы возникшим как наложение основно­го колебания u основной частоты и бесконечно многих гармонических колебаний u_v с частотами n_vf₁. Зависимость амплитуды отдельных колебаний от частоты представляет собой дискретный линейчатый спектр (рисунок 2.3). Наименьшая встре­чающаяся в линейчатом спектре частота — основная частота .

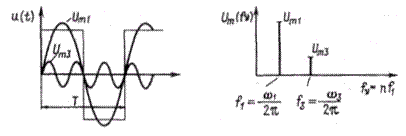
Рисунок 2.3 - Периодическая несинусоидальная функция

Частоты высших гармоник являются целыми кратными этой основной частоте, например f ₃ = 3 f ₁.

Будут ли иметь место синусоидальные, смешанные, косинусо­идальные с целыми или дробными гармониками функции, зави­сит от того, как описывается импульс во временной области: кривой, прямой или произвольной функцией.

Аналитически ряд Фурье любой функции времени может быть представлен в различных формах.

Нормальная:

(2.1)

где

(2.2)

(2.3)

(2.4)

Коэффициенты A_n и B_n – амплитуды отдельных колебаний. Составляющая U₀ соответствует среднему арифметическому зна­чению функции времени (постоянная составляющая).

Так как синусоидальные колебания соответствующим фазо­вым сдвигом могут быть представлены и как косинусоидальные, например sin(90° ± а) = cos a, вместо нормальной формы часто применяют амплитудно-фазовую форму:

Амплитудно-фазовая:

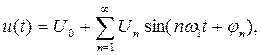(2.5)

где

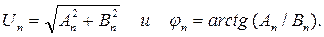(2.6)

Здесь U_n = f_n (nω ₁) - амплитудный спектр. Величину U_n (nω ₁) обычно измеряют спектральным анализатором; φ_n = f_φ (nω ₁) - фазовый спектр. Фазовый спектр используется в ЭМС редко в противоположность технике регулирования, на­пример, при рассмотрении вопросов устойчивости. Спектраль­ные амплитуды U_n измеряются в вольтах, I_n - в амперах и т.д.

Комплексная:

Если дополнять вышеприведенные уравнения мнимой частью и заменить тригонометрические функции по формуле Эйлера cos x + j sin x = e ^jx экспоненциальными функциями, получаем уравнение в комплексной форме

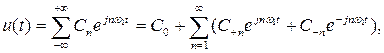(2.7)

где

(2.8)

где n = 0, ±1, ±2,...

Рисунок 2.4 – Амплитудный и фазовый спектры комплексного ряда Фурье

Так как левая часть (2.8) является действительной, то в пра­вой части должны быть введены отрицательные частоты (чтобы мнимые сократились). Учет отрицательных частот приводит к двустороннему спектру (рисунок 2.4). Идентичные вещественные части обоих слагаемых за знаком суммы (для положительных и отрицательных частот (± nω ₁) образуют физически измеримую ам­плитуду U_n. Сравнение коэффициентов при косинусах в (2.2) дает

| C_+n | + | C_-n | = U_n и C₀ = U₀.

C_n не идентична комплексной амплитуде переменного напря­жения соответствующей частоты nω ₁. В то время как при исполь­зовании последней напряжение u (t) является действительной ча­стью вектора

u (t)=Re{ U e^{j ωt} },

в комплексном ряде Фурье напряжение u (t) является результатом соответствующего наложения двух вращающихся в противопо­ложные стороны комплексных векторов, действительные части которых при сложении образуют амплитуду, а мнимые части не­прерывно взаимно сокращаются.

При анализе ЭМС вместо двустороннего математического спектра

C_n = f (± nω) чаще всего рассчитывают односторонний физический спектр

2| С_+n | = f (± nω) только для положительных n, амплитуды которого отличаются на коэффициент 2 от амплитуд двустороннего спектра. Значения амплитуд одностороннего спек­тра измеримы, они совпадают со значениями коэффициентов косинусоидальной формы, т. е. соответствуют значительным час­тям векторов переменного напряжения той же частоты.

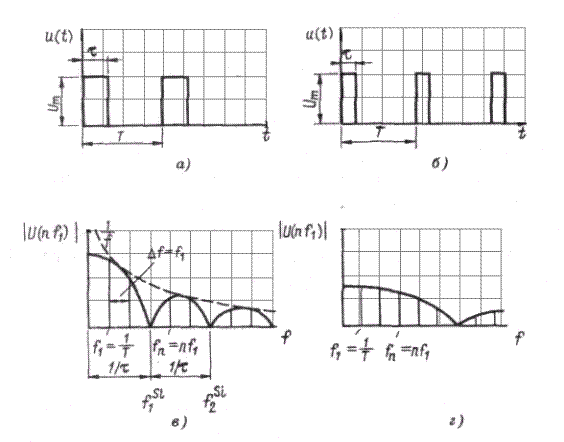
Рисунок 2.5 – Линейчатые спектры двух периодических прямоугольных импульсов напряжений со скважностью (1:2)

В заключение на рисунок 2.5 показаны импульсы прямоугольной формы двух периодически изменяющихся напряжений одной и той же основной частоты, однако различной скважности, и отно­сящиеся к ним линейчатые спектры. Из вышесказанного можно установить следующее.

Наименьшая частота f ₁ является основной частотой. Ее значе­ние связано со значением периода Т:

(2.9)

Амплитуды высших гармоник появляются с одинаковым ин­тервалом Δ f = =их частоты кратны основной частоте

f_n = nf ₁ (2.10)

Ряд Фурье для последовательности прямоугольных импульсов имеет вид

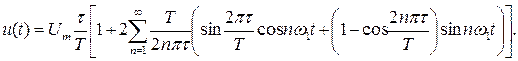
(2.11)

Коэффициенты (спектральные амплитуды) (без постоянной составляющей) определяются

(2.12)

Дата добавления: 2014-01-05