Бернулли считал, что большинство людей не склонны к риску

Полученные условия позволяют сделать вывод о виде функции рисковой полезности.

Учитывая, что функция рисковой полезности, возрастающая в случае, если лицо, принимающее решение, склонно к риску принимает вид

,

то функция U(V) является выпуклой.

Если лицо, принимающее решение, не склонно к риску, то имеем

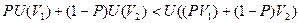
и функция U(V) вогнутая.

Если лицо, принимающее решение, безразлично к риску, то верно равенство

.

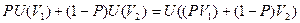Согласно аксиомам Дж. Неймана и О. Моргенштерна, которым должны удовлетворять рассматриваемые предпочтения лица, принимающего решения, этим предпочтениям можно поставить в соответствие екоторые количественные оценки, которые сохраняют порядок предпочтения и позволяют производить их сравнительный анализ путем сопоставления значений функции рисковой полезности. В изложении американского экономиста П. Шумейкера более поздний вариант этих аксиом выглядит следующим образом.

1. Аксиома порядка и транзитивности.

Порядок в системе предпочтений означает, что лицо, осуществляющее выбор между двумя простыми лотереями, может однозначно указать одно из трех соотношений: лотерея L₁ предпочтительнее лотереи L₂ или, наоборот, лотерея L₂ предпочтительнее лотереи L₁, или обе лотереи эквивалентны. Следовательно, возможно одно из трех соотношений:

.

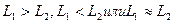Транзитивность означает, что если первая лотерея предпочтительнее второй, а вторая предпочтительнее третьей, то первая лотерея предпочтительнее третьей, т.е.,

.

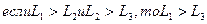2. Аксиома устойчивости.

Если значения V₁, V₂ и V₃ таковы, что 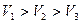, то существует вероятность , при которой простая лотерея .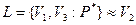

3. Аксиома доминирования.

Если две лотереи с одинаковыми выигрышами и разными вероятностями их получения имеют вид

,

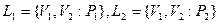причем 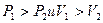, то первая лотерея всегда предпочтительнее второй: .

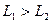4. Аксиома заменяемости.

Пусть из двух проектов с гарантированными доходами V₁ и V₂ для некоторого лица проект 1 привлекательнее проекта 2. Тогда для любой вероятности P и при любом значении дохода V лотерея 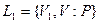всегда привлекательнее лотереи 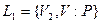, т.е .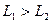

5. Аксиома последовательности.

Любая составная лотерея, в которой каждый исход сам является лотереей, эквивалентна лотерее с несколькими исходами, вероятности наступления которых определяются путем перемножения вероятностей всех возможных состояний по правилу произведения вероятностей сложных событий.

Пусть

.

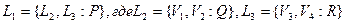Тогда лотерея

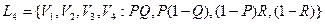
эквивалентна лотерее L₁, т.е. .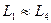

Используя приведенные пять аксиом, можно показать, что существует порядковая функция рисковой полезности, такая, что упорядочение лотерей по ожидаемой полезности их выигрыша соответствует действительным предпочтениям лица, принимающего решения, если оно в своих действиях учитывает аксиомы 1-5.

Если принять все пять аксиом, то можно доказать следующую теорему.

Возможно каждому исходу i=1,…,n приписать число u_i такое, что для любых двух лотерей 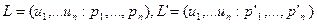будет верно 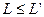, если и только если .

Число u_i, приписанное i – му исходу, называется его полезностью. Число же 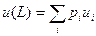, которое приписывается лотерее L_, называется средней ожидаемой полезностью этой лотереи. С точки зрения теории вероятностей это просто математическое ожидание лотереи.

Дата добавления: 2014-01-05