Непрерывное наращение и дисконтирование

Все рассмотренные ранее начисляемые проценты называются дискретными, поскольку их начисление осуществляется за фик­сированный промежуток времени (год, квартал, месяц, день, даже час). Уменьшая этот промежуток (период начисления) и увеличивая частоту начисления процентов, в пределе можно перейти к так называемым непрерывным процентам.

Уже отмечалось, что в зависимости от частоты начисления процентов наращение суммы осуществляется различными тем­пами, причем с возрастанием частоты накопленная сумма при использовании процентной ставки увеличивается. Максимально возможное наращение осуществляется при бесконечном дроб­лении годового интервала. Из формулы при 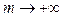сле­дует:

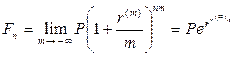(5.17)

так как согласно второму замечательному пределу 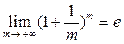, где трансцендентное число 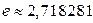называется числом Эйлера и является одной из важнейших по­стоянных математического анализа.

Чтобы отличить непрерывную ставку от обычной (дискрет­ной), вводят специальное обозначение непрерывной ставки - 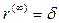и называют ее силой роста (force of interest). Таким образом, формула (5.17) для нахождения наращенной суммы за лет при непрерывном начислении процентов принимает вид:

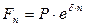(5.18)

где 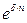является множителем наращения, причем этой формулой пользуются и в тех случаях, когда не является целым числом.

Очевидно, что F_l, F₂,..., F_{n ,} определяемые по формуле (5.18), образуют геометрическую прогрессию со знаменателем .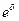

Аналогично другим множителям наращения е равен индексу роста суммы Р за лет.

Пример:

Рассчитать накопленную сумму для различных вариантов начисления процентов за один год, если исходная сумма Р = 1000 тенге и номинальная годовая процентная ставка .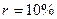

Результаты, полученные для некоторых вариантов, приведем в виде таблицы, причем в предпоследнем столбце вычислены разности между наращениями с данным числом начисления процентов и базовым, а в последнем столбце указаны разности между наращенными суммами двух соседних строчек.

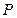
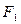
	Частота начисления		Наращение
базовое	цепное
	Ежегодное	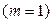1100,00	-	-
	Полугодовое	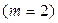1102,50	+2,50	+2,50
	Квартальное	1103,81	+3,81	+1,31
	Ежемесячное	1104,71	+4,71	+0,90
	Ежедневное	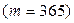1105,16	+5,16	+0,45
	Непрерывное	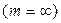1105,17	+5,17	+0,01

Как и следовало ожидать, приведенные расчеты подтвер­ждают наличие прямой зависимости между частотой начисле­ния процентов и накопленной суммой; последний столбец таб­лицы показывает, что с увеличением частоты начисления темп прироста накопленной суммы уменьшается.

При дискретном наращении каждая "ступенька" характеризует прирост основной суммы в результате очередного начисления, причем величина "ступеньки" все время возрастает. В рамках одного года одной "ступеньке" на левом графике со­ответствуют две "ступеньки" на среднем графике меньшего размера, однако в сумме они превышают эту "ступеньку" одно­кратного начисления. Таким образом, ордината точки, соответ­ствующей концу трехлетнего периода, на среднем графике бу­дет выше, чем на левом. Еще более быстрым темпом идет нара­щение при непрерывном начислении, что и показывает график справа.

Сила роста S характеризует интенсивность наращения за год при непрерывном начислении процентов. Можно сказать, что S показывает скорость относительного роста накапливаемой сум­мы. Поясним это. Пусть в течение времени на сумму Р на­числяются непрерывные проценты по ставке S. Тогда за время первоначальная сумма увеличится на относительную величи­ну

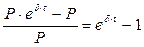
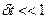и, следовательно, в единицу времени относительный прирост равен , что является средней скоростью относительного роста накапливаемой суммы за время . Ну а поскольку при справедлив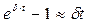о , то .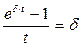

Приравнивая накопленные суммы, получим связь между силой роста и годовой процентной став­кой . Из 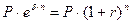следует, что

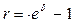, или 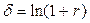(5.19)

Аналогичным образом, приравнивая накопленные суммы, получим связь между силой роста и годовой учетной ставкой:

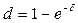, или 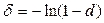(5.20)

Для малых 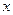справедливо

;

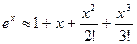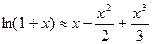
с точностью до членов третьего порядка малости, пренебрегая которыми и используя (5.19), (5.20), получим для 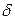, и 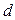, не превышающих 20%:

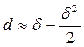и

и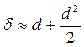

А при ставках до 10% сила роста и годовая ставка совпадают с точностью до 0,01, т.е. можно в этих пределах использовать приближенные равенства 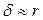и .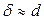

Пример:

На сумму в 2 тыс. тенге начисляются непрерывные проценты по ставке 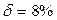. Определить наращенную сумму через 5 лет.

По формуле (5.18), полагая 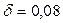, сразу получим 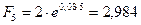тыс. тенге. Если в данном случае применить формулу (3.1), т.е. осуществлять начисление обычных сложных процентов по ставке 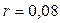, то получим сумму, не сильно от­личающуюся от вычисленной: 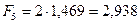тыс. тенге.

Если наращение сложными процентами осуществляется по номинальной годовой учетной ставке 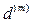, то при 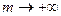следует:

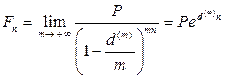
Полученная формула при 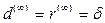совпадает с (5.17), т.е. исчезает различие между антисипативным и декурсивным способами начисления процентов, если использовать непрерыв­ное начисление и капитализацию. Это и естественно, так как в такой ситуации начало и конец периода перестают отличаться.

Из формулы (5.17) можно определить современную стои­мость величины :

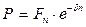(5.21)

Аналогичное равенство, естественно, получается и из форму­лы для определения стоимости капитала, учтенного за лет при 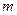-кратном дисконтировании в течение года при 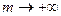. В этом случае S называется силой учета (force of discount) и показывает скорость относительного уменьшения учитываемой (при непрерывном дисконтировании) суммы. Та­ким образом, сила роста равна силе учета.

Пример:

Какую сумму необходимо поместить на банковский депозит, чтобы через 3 года получить 5 тыс. тенге, если происходит не­прерывное начисление процентов по ставке ?

Используем формулу (5.21):

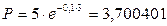тыс. тенге.

Из равенства (5.18) или равносильного ему (5.21) можно оп­ределить срок или силу роста соответственно по форму­лам:

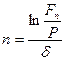и (5.22)

Пример:

За какой срок сумма в 400 тыс. руб. достигнет величины 1 млн. тенге при непрерывном начислении процентов и силе роста 10%?

Полагая 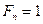; ; 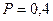получим

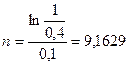года,

т.е. срок равен 9 годам и двум месяцам (точнее, 59,46 дням, если в году 365 дней).

Непрерывное начисление процентов используется при анали­зе сложных финансовых задач (например, при обосновании и выборе инвестиционных решений). Оценивая работу финансо­вого учреждения за период, в котором платежи поступают мно­гократно, бывает целесообразно предполагать, что накапливае­мые суммы непрерывно меняются во времени, и применять не­прерывное начисление процентов.

Бывают ситуации, когда непрерывное начисление процентов применяется и непосредственно при работе с клиентами. Так, в начале 1975г. в США ставка процентных выплат по займам и депозитам сроком от шести до десяти лет была ограничена величиной 7,75% годовых, однако не лимитировалось число начислений процентов в течение года, чем и воспользовались компании в целях привлечения вкладчи­ков. Причем одна из компаний предлагала непрерывное начис­ление процентов при годовой ставке 7,75%, которая в этих ус­ловиях стала непрерывной и представляла собой силу роста.

Обозначая 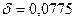, получим 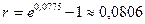, т.е. ком­пания, по существу, установила процентную годовую ставку .

Предположим теперь, что сила роста меняется и в следую­щих друг за другом периодах, длительностями (измеряемыми в годах) сила роста равна соответственно По формуле (5.18) для наращенной суммы за период по­лучим

;

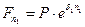далее наращение суммы непрерывными процентами за пе­риод 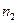составит величину

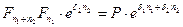
Окончательно за период 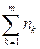наращенная сумма составит

(5.23)

Обозначая 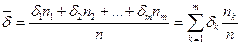, получим 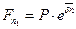. Таким образом, если за силу роста принять взве­шенную сумму сил роста , то наращенную сумму в этом случае можно находить не по формуле (5.23), а по формуле (5.18). Обратим внимание, что похожая ситуация была и в ана­логичном случае для простых процентов.

Пример:

На вклад в 2 тыс. руб. начисляются непрерывные проценты. Найти наращенную сумму за 7 лет, если сила роста изменяется следующим образом: в первые два года равна 8%, в следующие три года - 10% и в каждый оставшийся год увеличивается на 0,5%.

Так как ,

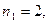
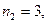
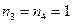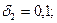
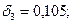
то по формуле (5.23):

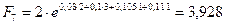тыс. тенге.

Такую же наращенную сумму получим, если непрерывные проценты начисляются за 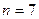лет при силе роста

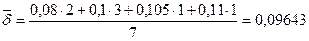или .

В общем виде силу роста, изменяющуюся во времени, можно обозначить как 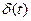(время, как это принято часто в высшей математике, будем обозначать через , а не через ). Через 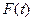обозначим накопленную сумму в момент , а 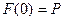представляет собой первоначальный капитал, напри­мер, положенный на депозит при . Можно показать, что в случае интегрируемости 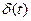справедливо равенство

,

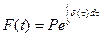из которого следует, что современная стоимость определяется по формуле .

Задавая конкретный вид 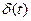, можно получить формулы для определения наращенных сумм в момент времени t при исполь­зовании различных ставок. Например, полагая , получим формулу наращения сложными процентами по про­центной ставке . Подобным образом можно получить все из­вестные формулы. Рассмотрим некоторые другие варианты.

1. Сила роста является кусочно-постоянной функцией:

Найдем вид 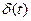при различных значениях t.

Пусть , тогда

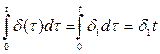
Пусть 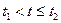, тогда

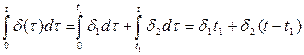
Рассматривая аналогичным образом остальные промежутки времени, для последнего из них 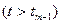, получим:

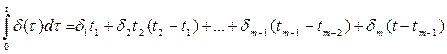
В частности, если 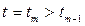, то, обозначая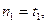 …, получим формулу (5.18), т.е. если сила роста кусочно-постоянна, то в любой момент вре­мени наращенная сумма, по существу, определяется по (5.18).

Пример:

Найти величину множителя наращения за 4 года, если сила роста изменяется непрерывным образом с годовым приростом в 1% и начальное значение силы роста составляет 9%.

В данном случае 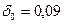и за год ставка увеличивается в а = 1,01 раза. Поскольку 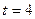, и то множитель наращения равен величине .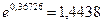

Дата добавления: 2014-01-05