Лекция 3. Матрицы. Операции над ними

Матрицы. Операции над ними

Матрицей называется множество чисел, образующих прямоугольную таблицу, которая содержит m строк и n столбцов. В общем виде матрица записывается следующим образом:

	a11	a12	…	a1n
A=	a21	a22	…	a2n	(1)
…	…	…	…
	am1	am2	…	amn

Для любого элемента (члена) матрицы a _ij, как и в случае определителей, первый индекс i означает номер строки, а второй индекс j – номер столбца. Сокращённо матрицу записывают так:

A = (a _ij ), где i = 1, 2,...,m, j = 1, 2, … n.

Виды матриц

Если в матрице число строк не равно числу столбцов (m ≠ n), то матрица называется прямоугольной. Таковы, например, матрицы

	a11	a12
А=	a21	a22				B=	a11	a12	a13
a31	a32				a21	a22	a23
	a41	a42

Если число строк равно числу столбцов (m = n), то матрица называется квадратной. Например, квадратными являются матрицы

А=	а11	а12			B=	а11	а12	а13
а21	а22	,		а21	а22	а23
					а31	а32	а33

Число строк и столбцов квадратной матрицы называют её порядком. В приведённом примере порядок матрицы А равен 2, а порядок матрицы В равен 3.

Рассмотрим квадратную матрицу порядка n:

	a11	a12	…	a1n
A=	a21	a22	…	a2n	(2)
…	…	…	…
	an1	an2	…	ann

Она называется невырожденной (неособой), если её определитель D_A не равен нулю. Если же D_A = 0, то матрица – особая (вырожденная). Диагональ, содержащую элементы a₁₁, a₂₂, … a_nn, как и в теории определителей, называют главной, а диагональ с элементами a_1n, a_{2, n-1}, … a_n1 – побочной.

Матрицы, у которых отличны от нуля только элементы, находящиеся на главной диагонали, называют диагональными. Например, матрицы

A =			и	B =
		-5

являются диагональными матрицами соответственно второго и третьего порядка. Если у диагональной матрицы все элементы главной диагонали равны между собой, т.е. a₁₁ = a₂₂ = … a_nn, то такая диагональная матрица называется скалярной. Если в скалярной матрице все элементы главной диагонали равны единице, то матрица называется единичной и обозначается буквой E. Так, единичной матрицей третьего порядка является матрица

Е =

Если в матрице (1) m = 1, n > 1, то получим матрицу-строку (однострочечную матрицу)

A = (a₁₁ a₁₂ … a_1n) (3)

Если же m > 1, а n = 1, то получается матрица-столбец (одностолбцевая матрица)

	b11
В=	b21
…
	bm1

Матрицы-строки и матрицы-столбцы называют также вектор-строкой и вектор-столбцом.

Матрица А^Т (или А^*) называется транспонированной по отношению к матрице А, если столбцы матрицы А являются строками матрицы А^Т. Так, матрица

	a11	a21	…	am1
A^T=	a12	a22	…	am2	(5)
…	…	…	…
	a1n	a2n	…	amn

является транспонированной по отношению к матрице (1). Квадратная матрица А называется симметричной относительно главной диагонали, если a _ij = a _ji. Очевидно, что симметричная матрица совпадает со своей транспонированной.

Равенство матриц

Две матрицы А = (a _ij ) и В = (b _ij ) называются равными, если равны элементы, стоящие на одинаковых местах, т.е. если a _ij = b _ij при всех i и j. При этом число строк и столбцов матриц А и В должно быть одинаковым. Так, матрицы

A=	a11	a12		и		B=	b11	b12
a21	a22			b21	b22

равны, если

a₁₁ = b₁₁, a₁₂ = b₁₂, a₂₁ = b₂₁, a₂₂ = b₂₂.

Равные матрицы имеют одну и ту же структуру: обе они либо прямоугольные (m x n), либо квадратные одного и того же порядка n.

Линейные операции над матрицами

Матрицы можно складывать, умножать на число и друг на друга. Рассмотрим эти операции.

Суммой двух матриц А = (a _ij ) и В = (b _ij ) называется матрица С = (c _ij ), элементы которой определяются равенством:

a _{ij +} b _ij = c _ij (i = 1, 2, … m; j = 1, 2, … n).

Аналогично определяется разность двух матриц. Складывать можно только матрицы, имеющие одинаковую структуру: или прямоугольные типа (m x n) или квадратные порядка n.

Пример 1.

a11	a12	+	b11	b12	=	a11+b11	a12+b12
a21	a22	b21	b22	a21+b21	a22+b22

Так как сложение матриц сводится к сложению их элементов, являющихся числами, то на него распространяются переместительный

А + В = В + А (6)

и сочетательный

(А + В) + С = А + (В + С) (7)

законы сложения.

Произведением матрицы А = (a _ij ) на число k называется матрица, у которой каждый элемент равен произведению соответствующего элемента матрицы А на число k:

kА = k(a _ij ) = (ka _ij ) (i = 1, 2, … m; j = 1, 2, … n)

Пример 2.

k	a11	a12	=	ka11	ka12
a21	a22	ka21	ka22

Произведение матриц

Рассмотрим умножение квадратных матриц второго порядка

A=	a11	a12		и			В=	b11	b12
a21	a22				b21	b22

Произведение обозначается так: A ^. B = C (или AB = C).

Чтобы найти элемент с₁₁ первой строки и первого столбца матрицы С, нужно каждый элемент первой строки матрицы А (a₁₁ и а₁₂) умножить на соответствующий элемент первого столбца (b₁₁ и b₂₁) и полученные произведения сложить: c₁₁ = а₁₁b₁₁ + a₁₂b₂₁;

чтобы найти элемент с₁₂ первой строки и второго столбца матрицы С, нужно умножить все элементы первой строки (а₁₁ и а₁₂) на соответствующие элементы второго столбца (b₁₂ и b₂₂) и полученные произведения сложить: с₁₂ = а₁₁b₁₂ + a₁₂b₂₂.

Аналогично находятся элементы с₂₁ и с₂₂.

С = AB =	a11b11 + a12b21	a11b12 +a12b22
a21b11 + a22b21	a21b12 + a22b22

Сформулируем правило умножения двух матриц.

Произведением матрицы А = (а _ij ), имеющей m строк и k столбцов, на матрицу В = (b _ij ), имеющей k строк и n столбцов, называется матрица С = (с _ij ), имеющая m строк и n столбцов, у которой элемент с _ij равен сумме произведений элементов i -ой строки (a _i1, a _i2, … a _in ) матрицы А на соответствующие элементы j -го столбца (b _1j, b _2j, … b _nj ) матрицы В.

Согласно этому правилу, число столбцов матрицы А должно быть равно числу строк матрицы В. В противном случае произведение не определено.

Пример 3.

a11	a12	a13	b11	b12	b13
a21	a22	a23 ^.	b21	b22	b23 =
			b31	b32	b33

a11b11 + a12b21 + a13b31	a11b12 + a12b22 + a13b32	a11b13 + a12b23 + a13b23
a21b11 + a22b21 + a23b31	a21b12 + a22b22 + a23b32	a21b13 + a22b23 + a23b33

Пример 4. (Кристина Владимирова, ТШ-062).

Найти произведение матриц

А =		-3		и В =
	-4
	-5

Найдём каждый элемент матрицы-произведения:

c₁₁ = a₁₁b₁₁ + a₁₂b₁₂ + a₁₃b₁₃ = 1 ^. 2 + (-3) ^. 1 + 2 ^. 1 = 1

c₁₂ = a₁₁b₁₂ + a₁₂b₂₂ + a₁₃b₃₂ = 1 ^. 5 + (-3) ^. 2 +2 ^. 3 = 5

c₁₃ = a₁₁b₁₃ + a₁₂b₂₃ + a₁₃b₃₃ = 1 ^. 6 + (-3) ^. 5 + 2 ^. 2 = -5

c₂₁ = a₂₁b₁₁ + a₂₂b₂₁ + a₂₃b₃₁ = 3 ^. 2 + (-4) ^. 1 + 1 ^. 1 = 3

c₂₂ = a₂₁b₁₂ + a₂₂b₂₂ + a₂₃b₃₂ = 3 ^. 5 + (-4) ^. 2 + 1 ^. 3 = 10

c₂₃ = a₂₁b₁₃ + a₂₂b₂₃ + a₂₃b₃₃ = 3 ^. 6 + (-4) ^. 5 + 1 ^. 2 = 0

c₃₁ = a₃₁b₁₁ + a₃₂b₂₁ + a₃₃b₃₁ = 2 ^. 2 + (-5) ^. 1 + 3 ^. 1 = 2

c₃₂ = a₃₁b₁₂ + a₃₂b₂₂ + a₃₃b₃₂ = 2 ^. 5 + (-5) ^. 2 + 3 ^. 3 =9

c₃₃ = a₃₁b₁₃ + a₃₂b₂₃ + a₃₃b₃₃ = 2 ^. 6 + (-5) ^. 5 + 3 ^. 2 = -7

Следовательно,

АВ =			-5
		-7

Далее Кристина находит произведение ВА:

ВА =	2 ^. 1 + 5 ^. 3 + 6 ^. 2	2(-3) + 5(-4) + 6(-5)	2 ^. 2+ 5 ^. 1 + 6 ^. 3
1 ^. 1 + 2 ^. 3 + 5 ^. 2	1(-3) + 2(-4) + 5(-5)	1 ^. 2+ 2 ^. 1 + 5 ^. 3	=
1 ^. 1 + 3 ^. 3 + 2 ^. 2	1(-3) + 3(-4) + 2(-5)	1 ^. 2+ 3 ^. 1 + 2 ^. 3

=		-56
	-36	19
	-25

Видим, что АВ ≠ ВА. Этот пример показывает, что произведение двух матриц, вообще говоря, не подчиняется переместительному закону.

Путём непосредственной проверки можно убедиться в справедливости следующих соотношений для матриц:

(А + В) ^. С = А ^. С + В ^. С (8)

С ^. (А + В) = С ^. А + С ^. В (9)

А ^. (В ^. С) = (А ^. В) ^. С (10)

Завершая анализ операций над матрицами, рассмотрим пример вычисления матричного многочлена.

Пример 5. (Маша Куприянова, ТШ-061).

Найти значение матричного многочлена

3(А² – В²) – 2АВ

при	А =		-2			и		В =		-7	-2
			-1								-1

Имеем

А^2 =		-2			-2		=
		-1			-1			-3
				2
В^2 =		-7	-2 ^.		-7	-2	=	-27
			-1			-1

А^2 – В^2 =		-39	-23	, 3(А^2 – В^2) =		-117	-69
	-4				-12

				2				19	-14
АВ =		-2	0 ^.		-7	-2	=	-4			,
		-1				-1		-3

	38	-28
2 АВ =	-8
	-6

3(A^2 – B^2) – 2 AB =		-145	-89
	-6	-14

Умножение на единичную матрицу

На основании правила умножения матриц получаем:

АЕ =	а11	а12 ^.			=	а11	а12
а21	а22			а21	а22

EA =		0 ^.	а11	а12	=	а11	а12
		а21	а22	а21	а22,

т.е. АЕ = ЕА = А (11)

Произведение квадратной матрицы любого порядка на соответствующую единичную матрицу равняется первоначальной матрице. Таким образом, при умножении матриц единичная матрица играет роль единицы, поэтому и называется единичной.

Понятие обратной матрицы

Если А – квадратная матрица, то обратной по отношению к А называется матрица, которая, будучи умноженной на А (как справа, так и слева), даёт единичную матрицу. Обозначив обратную матрицу через А^-1, запишем

А^-1А = АА^-1 = Е (12)

Если обратная матрица А^-1 существует, то матрица А называется обратимой. Операция вычисления обратной матрицы называется обращением матрицы. Для того, чтобы квадратная матрица А имела обратную, необходимо и достаточно, чтобы матрица А была невырожденной.

Нахождение матрицы, обратной данной

Пусть дана невырожденная матрица

	а11	а12	а13
А=	а21	а22	а23
	а31	а32	а33

	а11	а12	а13
DА =	а21	а22	а23	≠ 0
	а31	а32	а33

Обратной матрицей А^-1 будет матрица

	A11/DА	A21/DА	A31/DА
A^-1 =	A12/DА	A22/DА	A32/DА	,		(13)
	A13/DА	A23/DА	A33/DА

где А _ij – алгебраическое дополнение элемента а _ij определителя D_A.

Убедиться в этом можно, умножая матрицу А на матрицу А^-1. Например, элементы с₁₁ и с₂₃ определяются так:

···

c ₂₃ =a ₂₁···=

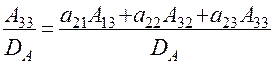== 0

В итоге

	а11	а12	а13	A11/DА	A21/DА	A31/DА
С=AA^-1=	а21	а22	а23	A12/DА	A22/DА	A32/DА	=				=E
	а31	а32	а33	A13/DА	A23/DА	A33/DА

Матрица

	A11	A21	A31
=	A12	A22	A32			(14)
	A13	A23	A33

называется матрицей, присоединённой к А. (Используется также обозначение ). Обратная матрица А^-1 через присоединённую 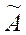выражается так:

=	1		(15)
DA

Обратную матрицу будем находить по следующей схеме:

1. Находим определитель матрицы А.

2. Находим алгебраические дополнения всех элементов а _ij матрицы и записываем новую матрицу.

3. Меняем местами строки и столбцы полученной матрицы (транспонируем матрицу).

4. Умножаем полученную матрицу на 1/D_A.

Пример 6. (Лена Иванова, КШ-061).

Дана матрица

A =
		-2	-3

Найти обратную матрицу.

1. Вычисляем определитель матрицы А:

DA =				=		-12	-17	=	(492 - 493) = -1
		-2	-3			-29/2	-41/2

Так как D_A ≠ 0, то матрица А является невырожденной, и, значит, можно найти матрицу А^-1.

2. Находим алгебраические дополнения элементов этого определителя:

A11 =			= -1,	A21 = -			= 1,	A31 =			= -1,
-2	-3	-2	-3

A12 = -			= 38,	A22 =			= -41,	A32 = -			= 34,
	-3		-3

A13 =			= -27,	A23 =-			= 29,	A33 =			= -24.
	-2		-2

Следовательно,

	-1		-1			-1
A ^-1 = (-1)		-41		=	-38		-34
	-27		-24			-29

Лекция 4.

Применение теории матриц к решению и исследованию систем линейных уравнений

Снова рассмотрим систему трёх линейных уравнений первой степени с тремя неизвестными (см. (1), лекция 2).

а11x1 + a12x2 + a13x3 = b1
а21x1 + a22x2 + a23x3 = b2		(1)
а31x1 + a32x2 + a33x3 = b3

Введём три матрицы:

	а11	а12	а13
А=	а21	а22	а23
	а31	а32	а33

	х1
X =	х2
	х3

	b1
B =	b2
	b3

Используя правило умножения матриц, систему (1) запишем в матричной форме

	а11	а12	а13	х1			b1
B =	а21	а22	а23	х2		=	b2			(2)
	а31	а32	а33	х3			b3

или

AX = B (3)

Это равенство называется простейшим матричным уравнением. Для его решения умножим левую и правую часть слева на матрицу А^-1:

А^-1АX = A^-1B

Так как А^-1A = E, а EX = X, то

X = A^-1B (4)

или в развёрнутом виде

x1			A11	A21	A31	b1
x2	=	1/DA	A12	A22	A32 ^.	b2		(5)
x3			A13	A23	A33	b3

Произведя умножение матриц, находим

x1			b1A11 + b2A21 + b3A31
x2	=	1/DA	b1A12 + b2A22 + b3A32
x3			b1A13 + b2A23 + b3A33

Приравнивая элементы матриц, стоящих слева и справа, получаем

x1 =	b1A11 + b2A21 + b3A31
DA

x2 =	b1A12 + b2A22 + b3A32
DA

x3 =	b1A13 + b2A23 + b3A33
DA

Это решение можно записать в форме определителей:

= =

=

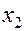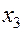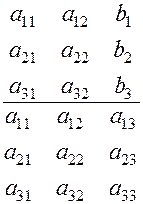
Пример 1. (Маша Куприянова).

Решить систему уравнений:

4x₁ + x₂ – x₄ = -9,

x₁ - 3x₂ + 4x₃ = -7,

3x₂ - 2x₃ + 4x₄ = 12,

x₁ + 2x₂ – x₃ - 3x₄ = 0.

Представим её в виде матричного уравнения и запишем в

виде (3), где

				-1		x1		-9
A =		-3			, X =	x2	, B =	-7
		-2		x3
			-1	-3		x4

Решение матричного уравнения имеет вид (4). Найдём А^-1.

Имеем:

				-1			-7
DA =		-3			=		-5			=
		-2				-2
			-1	-3				-1	-3

=(-1) [(-7) ^. 26 + 4 ^. 29 – 11 ^. 5] = 121

Вычислим алгебраические дополнения элементов этого определителя:

	-3							-1					-1
A11=		-2		=38,	A21= -		-2		=-9,	A31=	-3			=-7,
		-1	-3				-1	-3				-1	-3
			-1										-1
A41= -	-3			=-22,	A12= -		-2		=-26,	A22=		-2		=38,
		-2					-1	-3				-1	-3
			-1					-1				-3
A32= -				=43,	A42=				=66,	A13=				=-29,
		-1	-3				-2						-3
			-1					-1					-1
A23= -				=61,	A33=		-3		=34,	A43=-		-3		=55,
			-3					-3

Дата добавления: 2014-01-05