Лекция 1. Жизненный цикл программного обеспечения

КЛАССИФИКАЦИЯ СИЛ, ДЕЙСТВУЮЩИХ В ЖИДКОСТИ

Поскольку жидкость обладает свойством текучести и легко деформируется под действием минимальных сил, то в жидкости не могут действовать сосредоточенные силы, а возможно существование лишь сил распределенных по объему (массе) или по поверхности. В связи с этим действующие на жидкости распределенные силы являются по отношению к жидкости внешними. По характеру действия силы можно разделить на две категории: массовые силы и поверхностные.

Массовые силы. Силы, действующие на каждую частицу жидкости с массой D М = rD V, то есть силы, распределенные по массе, называются массовыми (объемными). К ним относятся: сила тяжести, силы инерции (кориолисова сила инерции, переносная сила инерции). К массовым силам относятся также гравитационные силы, подчиняющиеся закону всемирного тяготения Ньютона (силы притяжения Луны и Солнца при рассмотрении водных масс морей и океанов Земли).

Массовые силы характеризуются плотностью распределения F_A или напряжением массовых сил. Если D V – элементарный объем, содержащий точку А (рис. 2.1), и D F – массовая сила, действующая на массу D М = rD V жидкости в этом объеме, то в данной точке А плотность распределения массовой силы при стягивании объема D V к точке А:

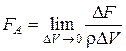. (2.1)

Таким образом, плотность массовой силы представляет собой массовую силу, отнесенную к единице массы. Ее составляющие по осям координат будут соответственно F_x, F_y, F_z. Плотность массовых сил имеет размерность ускорения (м/с²).

Определим вектор напряжения массовых сил в наиболее важном частном случае действия силы тяжести.

Вес элементарной частицы:

.

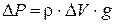При выборе направления оси Z вверх массовая сила:

,

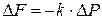где k – орт оси Z.

На основании (2.1) получаем:

.

Поверхностные силы. Силы, действующие на каждый элемент Dw поверхностей, ограничивающих жидкость, и на каждый элемент поверхностей, проведенных произвольно внутри жидкости, называются поверхностными. Поверхностные силы делятся на две группы: нормальные к поверхности силы и касательные к поверхности. К нормальным поверхностным силам относится сила давления D Р, к касательным поверхностным силам относится сила трения D Т.

Поверхностные силы, аналогично массовым силам, характеризуются плотностью распределения поверхностных сил или напряжением поверхностных сил. Различают нормальное напряжение в точке и касательное напряжение в точке.

Рассмотрим объем жидкости, выделим в объеме элементарную поверхность площадью Dw и наметим точку А (рис. 2.2). Пусть на выделенную поверхность действует нормальная сила D Р и касательная сила D Т. Тогда, плотность распределения нормальных сил определится как и называется нормальным напряжением в точке А. Плотность распределения касательных сил 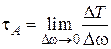– называется касательным напряжением в точке А.

Массовые и поверхностные силы могут быть внешними и внутренними. Внешние силы действуют на рассматриваемую массу и поверхность жидкости извне и приложены соответственно к каждой частице жидкости, составляющей массу, и к каждому элементу поверхности, ограничивающей жидкость. Внутренние силы представляют собой силы взаимодействия частиц жидкости. Они являются парными, их сумма в данном объеме жидкости всегда равна нулю.

Массовые силы, действующие в жидкости, влияют на гидродинамические реакции, возникающие на теле, через напряжения поверхностных сил.

2. СВОЙСТВА НАПРЯЖЕНИЙ ПОВЕРХНОСТНЫХ СИЛ,
ДЕЙСТВУЮЩИХ В ЖИДКОСТИ

Для исследования напряжений поверхностных сил в жидкости установим связь между напряжением, действующим на произвольно ориентированную площадку и три другие взаимно перпендикулярные площадки, проходящие через данную точку.

Выделим в движущейся жидкости элементарную жидкую частицу в форме тетраэдра (рис. 2.3). Вместо поверхностных сил на гранях тетраэдра изобразим векторы напряжений, направленные произвольным образом к соответствующим граням. Ускорение центра тяжести частицы обозначим , напряжение массовых сил .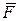

Запишем уравнение движения этой частицы в векторной форме, используя принцип Даламбера.

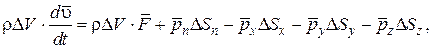
где D S_x, D S_y, D S_z – площади граней тетраэдра;

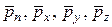– векторы напряжений поверхностных сил в центре площадок, обозначения которых соответствуют направлениям нормалей к ним, знак минус перед последними членами означает, что нормали к соответствующим площадкам направлены противоположно осям координат.

Из аналитической геометрии известно, что:

:

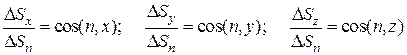Разделим обе части полученного уравнения на :

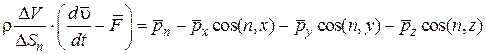
Чтобы получить связь между напряжениями в точке, устремим объем тетраэдра к нулю, стягивая его в точку к началу координат.

Очевидно, что , с учетом чего связь между напряжениями запишется в виде:

. (2.2)

Проектируя 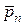на оси координат, получим:

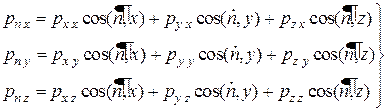
Первый индекс при проекциях напряжений в этих соотношениях соответствует площадке, в которой действует данное напряжение, а второй – оси, на которую оно проецируется. Скалярные величины р_хх, р_уу, p_zz представляют нормальные напряжения, все остальные (р_ху, p_xz, …) – касательные напряжения, действующие в определенных площадках.

В дальнейшем касательные напряжения будем обозначать буквой t:

р_ху = t _ху; р_хz = t _xz; …

Учитывая это, запишем:

Первое свойство: напряжения поверхностных сил, действующих по произвольной площадке в данной точки жидкости, зависят от девяти скалярных величин: трех нормальных напряжений (р_хх, р_уу, p_zz) и шести касательных ( t _ху, t _xz, t _yz, t _yx, t _zx, t _zy).

Такие величины в математике и механике носят название тензора, таким образом первое свойство напряжений поверхностных сил состоит в том, что эти напряжения образуют тензор напряжений.

.

На рис. 2.4 показаны нормальные и касательные напряжения, действующие на три взаимно перпендикулярные грани параллелепипеда, выделенные в жидкости.

Применяя теорему моментов, взятых относительно начала координат для напряжений, действующие на грани параллелепипеда, можно доказать свойство взаимности касательных напряжений, в соответствии с которым:

.

Из этого следует, что вследствие взаимности число независимых величин сокращается до шести.

Возникновение в жидкости касательных напряжений вызвано одновременным влиянием двух факторов: движение жидкости и ее вязкости.

Если жидкость неподвижна, то касательные напряжения в ней отсутствуют, что характерно как для вязких, так и для невязких жидкостей.

В покоящейся жидкости:

,

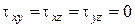то есть действуют только нормальные напряжения .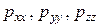

Соответствующие векторы напряжений:

.

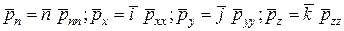Подставляя эти выражения в уравнение 2.2, получим:

.

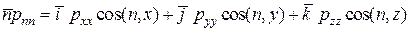Известно, что:

.

Подставляя предыдущее выражение в левую часть:

Сравнивая в этом выражении коэффициенты при одинаковых ортах, найдем:

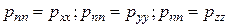
или .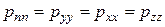

Эти равенства позволяют сформулировать теорему о свойстве нормальных напряжений:

Второе свойство: если в жидкости отсутствуют касательные напряжения, то нормальные напряжения в данной точке не зависят от ориентации площадки.

Рассмотрим одно из основных свойств жидкости, связанное с нормальными напряжениями.

Как видно из рис. 2.4, направлены в сторону внешней нормали, то есть нормальные напряжения – растягивающие, которым приписывается знак «+». Твердое тело одинаково воспринимает растягивающие и сжимающие напряжения, не меняя свое состояние. В нем при этом не образуется разрывов сплошности.

Третье свойство: капельная жидкость способна воспринимать произвольные сжимающие усилия (отрицательное нормальное напряжение) без разрыва сплошности. Однако жидкость практически терпит разрыв при растяжении, то есть в ней могут проявляться лишь нормальные сжимающиеся усилия.

Назовем давлением р в жидкости при отсутствии касательных напряжений величину нормального напряжения, взятую с обратным знаком, тогда, в соответствии с только что доказанной теоремой

,

отсюда следует, что величина давления не зависит от ориентации площадки.

3. УРАВНЕНИЯ ДВИЖЕНИЯ ЖИДКОСТИ В НАПРЯЖЕНИЯХ

Получим общее уравнение движения жидкости, устанавливающая связь между внешними и внутренними силами, действующими на нее.

Выделим в движущейся жид­кости поверхностью S произвольный жидкий объем V (рис. 2.5), а внутри него элементарную жидкую частицу с массой r× dV и поверхностью dS. К этой частице приложены массовые силы с напряжением 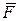и поверхностные силы с напряжением .

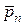Запишем уравнение движения этой частицы, обозначая ускорение ее центра тяжести :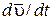

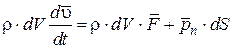
Просуммируем левую и правую часть уравнения. Суммирование первых двух членов сводится к интегрированию по объему, а третьего члена – по площади.

Согласно третьему закону Ньютона, поверхностные силы по всем внутренним площадкам взаимно уничтожатся, и останутся только поверхностные силы по площади S, ограничивающей объем V.

.

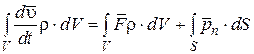Преобразуем третий член уравнения, используя для этого ранее полученную зависимость:

и получим:

Применим к правой части этого равенства известное преобразование Гаусса – Остроградского, устанавливающего связь между объемным и поверхностным интегралами:

Подставляя правую часть в уравнение, получим:

.

Все члены в этом уравнении интегрируются по объему. Это уравнение является уравнением движения жидкого объема в интегральной форме. Левая часть представляет главный вектор сил инерции, первый член правой части – главный вектор массовых сил, а второй – главный вектор поверхностных сил.

Получим дифференциальную форму уравнения движения, более удобную для изучения движения жидкости. Объединим все члены уравнения под знаком интеграла, перенося силу инерции в правую часть.

.

Интеграл равен нулю, когда подинтегральная функция равна нулю:

.

В итоге получим дифференциальное уравнение движения жидкости в напряжениях:

, (2.3)

которое связывает ускорение с напряжениями массовых и поверхностных сил в данной точке потока и справедливо как для вязкой, так и невязкой жидкости.

Проектируя векторное уравнение на оси координат, будем иметь:

Эта система уравнений служит для разработки гидростатики и гидродинамики вязкой и невязкой жидкости.

Дата добавления: 2014-01-05