Лекция 7. Элементы комбинаторики

Комбинаторика – это раздел математики, изучающий количество комбинаций, которые можно составить из заданного конечного множества попарно различных элементов произвольной природы.

Одно из важных правил комбинаторики – правило умножения:

если объект А может быть выбран из множества M _n h способами и при каждом выборе объекта А другой объект В может быть выбран k способами, то объект , состоящий из двух объектов А и В может быть выбран hk способами.

Конечные подмножества элементов множества M _n называются соединениями.

Если в совокупности соединений подмножества образованы только попарно различными элементами множества M _n, то такие соединения называются соединениями без повторений.

Если в совокупности соединений входят подмножества не только с попарно различными элементами множества M _n, но и с одинаковыми, то такие соединения называются соединениями с повторениями.

Различают три основных типа соединений: размещения, перестановки, сочетания.

Определение 7.1. Размещением из n элементов по m элементов без повторений называется упорядоченное подмножество попарно различных m элементов множества M _n ().

Определение 7.2. Перестановкой из n элементов без повторений называется упорядоченное множество всех n элементов множества M _n, то есть перестановка без повторений – это размещение без повторений из n по n элементов.

Определение 7.3. Сочетанием из n элементов по m элементов без повторений называется подмножество из m попарно различных элементов множества M _n без учёта порядка их следования ().

Для размещения или сочетания с повторениями 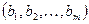требуется лишь условие, что и, следовательно, m может быть любым натуральным числом, независимым от числа n элементов множества M _n.

В перестановке с повторениями присутствуют все элементы множества M _n, причём указывается, сколько раз повторяются элементы . Число элементов в такой перестановке может быть любым натуральным числом, б о льшим или равным n.

Обозначим символами , , 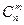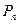число всех размещений, сочетаний без повторений из n элементов по m элементов и число всех перестановок без повторений из n элементов (). Символы для обозначения числа всех соединений определённого типа берутся из начальных букв соответствующих французских слов: arrangement – размещение, combination – комбинация, сочетание, permutation – перестановка.

Символами , , 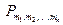обозначим число всех размещений, сочетаний, перестановок с повторениями (m, m_i – любые натуральные числа). Число m_i указывает, что элемент a_i повторяется в перестановке m_i раз, причем .

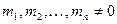Произведение n первых натуральных чисел обозначается символом n! и называется n -факториалом: .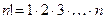

☼ По определению 0!=1 и 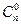=1. ☼

♦ Теорема 7.1. Число размещений без повторений из n элементов по m элементов вычисляется по формуле

, (7.1)

число размещений из n элементов по m элементов с повторениями

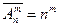. (7.2)

Доказательство. Докажем методом математической индукции формулы (7.1) и (7.2).

1) Для m =1 они справедливы, так как выбор по одному элементу из множества M _n можно осуществить только n способами, а по формулам (7.1) и (7.2) , .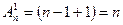

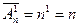2) Пусть эти формулы справедливы для произвольного фиксированного натурального числа k, то есть 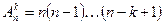, . По правилу умножения , , 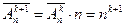так как в случае подмножества с попарно различными элементами множества M _n после выбора k элементов из M _n в нём останется n – k элементов, из которых по одному элементу можно выбрать n – k способами. А в случае размещения с повторениями (k +1)‑м элементом может быть любой из n элементов множества M _n. Учитывая, что , убеждаемся в справедливости формул (7.1) и (7.2). ■

Следствие 1. Так как , то . Таким образом, получается формула числа перестановок:

(7.3)

Формула для перестановок с повторениями такова:

. (7.3а)

Справедливость этой формулы установим следующими рассуждениями: если бы в перестановке все элементов были попарно различными, то таких перестановок было бы . Но, меняя между собой одинаковый элемент a_i любыми m_i! способами, мы не изменяем самой перестановки. Поэтому в знаменатель надо внести произведение факториалов .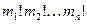

Следствие 2. По правилу умножения . Следовательно,

,

то есть справедлива формула

. (7.4)

♦ Теорема 7.2. Число сочетаний из n элементов по m элементов с повторениями вычисляется по формуле

. (7.5)

Доказательство. Докажем формулу (7.5) методом математической индукции.

1) Для m =1 она справедлива, так как , а выбор по одному элементу из множества M _n можно осуществить только n способами.

2) Пусть формула (7.5) верна для произвольного фиксированного 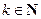, то есть 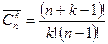. Тогда, по правилу умножения, 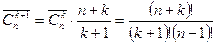, т.к. вставить один элемент, взятый из M _n, мы можем n + k способами, добавив к уже выбранным k элементам либо один из них, либо любой из M _n. А в знаменателе число k +1 означает, что вставить этот дополнительный элемент, не изменяя сочетания, мы можем либо вначале, либо между первым и вторым и т.д., либо после последнего (то есть k +1 вариантов).

Учитывая, что 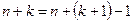, убеждаемся, что формула (7.5) справедлива для m = k +1, а значит, она справедлива и для любого натурального числа m. ■

♦ Теорема 7.3. Справедливо правило симметрии

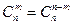. (7.6)

Доказательство. . ■

♦ Теорема 7.4. Справедлива формула (правило Паскаля)

. (7.7)

Доказательство.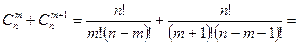

. ■

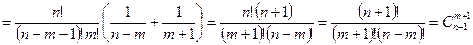♦ Теорема 7.5. Число всех подмножеств из n элементов равно :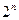

.

Доказательство. Докажем теорему методом математической индукции.

1) При n =1 имеем множество одного элемента 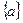, которое содержит два подмножества: пустое множество и само себя.

2) Пусть установлено, что множество из k элементов содержит ровно подмножеств.

Рассмотрим множество из k +1 элементов. Любое его подмножество В получается одним из двух способов:

а) берётся подмножество В множества ,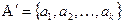

в) берётся подмножество 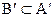и присоединяется элемент .

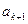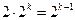Каждым из этих способов получаем подмножеств, а всего подмножеств множества А. ■

Рассмотрим несколько задач, решение которых осуществляется с использованием доказанных формул.

J Пример 7.1. Сколько пятизначных чисел можно составить из цифр 1, 3, 7?

Дата добавления: 2014-01-05