Момент инерции

Определим кинетическую энергию тела, совершающего вращательное движение. Для поступательного движения дело обстоит просто: т.к. все точки тела движутся с одинаковой скоростью , то кинетическая энергия будет определяться выражением , где 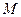масса всего тела.

Определим теперь кинетическую энергию вращательного движения. Для этого, мысленно разделим тело на элементарные объемы и будем считать их материальными точками. Если 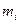масса 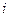-го элемента, а - кратчайшее расстояние этого элемента до оси вращения, то модуль его скорости будет равна , где - угловая скорость вращения тела. Кинетическая энергия этого элемента тела будет равна

.

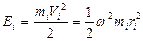Очевидно, полная кинетическая энергия вращения твердого тела определяется суммой кинетических энергий всех составляющих тело элементов, т.е.

,

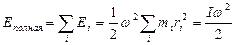где и зависит только от распределения массы тела относительно оси предполагаемого вращения. Эта величина называется моментом инерции. Как мы увидим в дальнейшем, момент инерции характеризует инерционные свойства тела способного вращаться и является аналогом массы при вращательном движении.

В общем случае, момент инерции находится интегрированием:

Пределы интегрирования определяются распределением массы тела относительно оси предполагаемого вращения, зависимостью 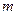от .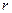

Рассмотрим некоторые частные случаи.

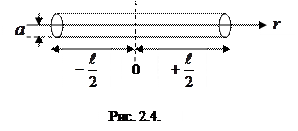
1. Вычислим момент инерции однородного длинного тонкого стержня (длина стержня 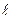, его масса 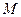), ось предполагаемого вращения которого перпендикулярна его оси симметрии и проходит через его центр инерции.

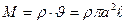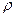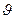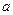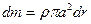Очевидно, масса стержня , где - плотность материала тела, - объем тела, - радиус стержня. Единственной переменной величиной зависящей от расстояния до оси вращения является длина, поэтому выражение для имеет вид: , где 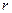- та переменная, по которой производится интегрирование. Пределы интегрирования определяются положением оси предполагаемого вращения. В данном случае 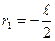, а . Поэтому:

Итак, для рассмотренного случая, .

2. Вычислим момент инерции однородного длинного стержня (длина стержня 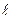, его масса 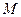), ось предполагаемого вращения которого перпендикулярна оси симметрии и проходит через его край (см. рис. 2.5).

Очевидно, что для решения этой задачи можно воспользоваться предыдущей, изменив только пределы интегрирования - . Вследствие этого имеем:

.

.

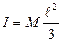3. Вычислим момент инерции однородного сплошного диска (радиус диска 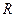, его масса 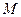), ось предполагаемого вращения которого проходит через его центр инерции и перпендикулярна его торцевой поверхности (см. рис. 2.6).

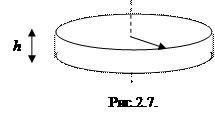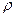Масса диска , где -плотность материала, из которого изготовлен диск, 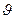- его объем, 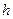- толщина диска. Единственной переменной величиной, зависящей от расстояния до оси вращения, является радиус, поэтому выражение для имеет вид: , где 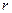- та переменная, по которой производится интегрирование. Пределы интегрирования определяются расположением оси предполагаемого вращения. В данном случае 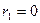, а . Поэтому:

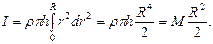
Итак, для рассмотренного случая имеем:

.

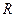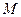4. Вычислим момент инерции однородного диска с центральным отверстием (внешний радиус - , радиус отверстия , масса - ), ось предполагаемого вращения которого проходит через его центр инерции и перпендикулярна его торцевой поверхности.

Как и ранее, для решения этой задачи воспользуемся предыдущей, изменив только пределы интегрирования - . Таким образом, имеем:

,

или, с учетом того, что масса диска с отверстием равна

.

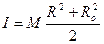5. Момент инерции однородного шара массой 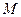и радиуса 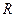определяется выражением:

.

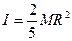Дата добавления: 2014-01-05