Уравнение неразрывности струи

Проследим течение жидкости в трубке тока (см. рис. 4.2). В общем случае, поперечное сечение трубки тока не одинаковое. Покажем, что произведение скорости идеальной жидкости на поперечное сечение трубки тока есть величина постоянная.

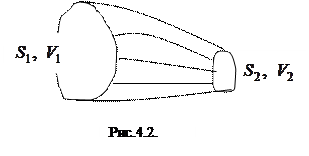Для доказательства используем факт, что струя нигде не претерпевает разрыва. Из этого следует, что объем жидкости, протекающей через сечение 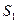за время 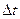, должен быть равен объему жидкости, протекающей через сечение за тоже время, т.е. или

.

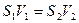4.2. Уравнение Бернулли

Каждый элемент жидкости обладает кинетической и потенциальной энергией. Изучим перенос энергии жидкостью, текущей в данной трубке тока. Поток будем считать установившимся.

Пусть за время 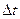через сечение 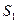проходит масса жидкости 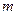. Кинетическая энергия, которая переносится через это сечение за время 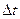, равна 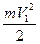. Через это сечение также переносится и потенциальная энергия, равная 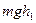, где 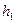высота рассматриваемого сечения трубки тока над уровнем моря. Таким образом, жидкость переносит через сечение 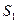за время 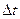энергию, равную 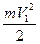+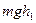. К этой сумме необходимо прибавить еще работу, которую совершает жидкость текущая сзади по проталкиванию рассматриваемого элемента жидкости через сечение 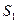, , 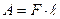но (), а . Следовательно, эта работа равна .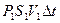

Итак, полная энергия, переносимая через сечение 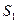за время 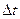, равна:

++.

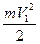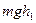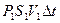Ввиду стационарности потока величина переносимой энергии остается неизменной в любом сечении трубки тока, поэтому для сечени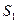й и можем записать:

++=++.

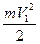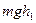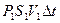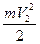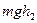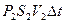Справа и слева стоит одинаковая масса, т.к. сколько массы жидкости или газа вошло через одно сечение трубки тока за время , столько же должно выйти через любое другое ее сечение за тоже время (жидкость (газ) считается несжимаемой).

Теперь воспользуемся уравнением непрерывности, из которого следует, что =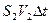. Разделим левую часть уравнения на , а правую на 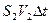. В результате получаем уравнение, получившее название уравнение Бернули:

++=++.

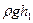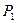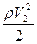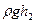Величина 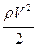называется динамическим давлением, а - статическим.

Для горизонтальной трубки тока уравнение Бернулли имеет вид:

+=+.

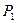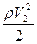Видно, что увеличение скорости потока жидкости (газа) сопровождается уменьшением статического давления. Таким образом, при сужении трубки тока скорость потока жидкости (газа) возрастает, а статическое давление уменьшается.

Статическое давление может быть определено по высоте поднятия жидкости в трубке, срез которой параллелен линиям тока.

Полное давление измеряется с помощью трубки Пито. Срез трубки перпендикулярен линиям тока. В трубке Пито высота поднятия жидкости определяется суммой статического и динамического давлений (см. рис.4.3).

При очень больших скоростях движения жидкости может возникнуть ситуация, когда статическое давление станет равным нулю и даже отрицательным. В результате струя начнет разрывать саму себя. Это явление называется кавитацией и ограничивает скорость, которая может быть достигнута в данной жидкости.

Эффект уменьшения статического давления в потоке жидкости используют в водоструйных насосах.

Область применимости уравнения Бернулли определяется предположениями, сделанными при его выводе: жидкость (газ) должна быть идеальной - невязкой и несжимаемой. Второе условие для жидкостей практически всегда выполняется, а применительно к газам – оно справедливо при не слишком больших скоростях (до (500-600) 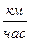). Первое же условие сильно ограничивает область применимости. Действительно, часть кинетической энергии жидкости вблизи стенок расходуется на преодоление сил трения (вязкость). Скорость течения в этих областях уменьшается и происходит нагрев жидкости и стенок. Поэтому к сильно вязким жидкостям, таким как глицерин, различные масла при относительно низких температурах, уравнение Бернулли неприменимо.

4.3. Течение вязкой жидкости

Изучим более подробно, как сказывается вязкость жидкости на характере ее течения.

Чтобы установить степень вязкости среды, представим себе следующий опыт. Две пластинки разделены слоем жидкости. Одна пластинка покоится, другая движется. Слой жидкости, находящийся вблизи неподвижной пластинки, практически неподвижен. Слой жидкости, находящийся вблизи движущейся пластинки, движется с ее скоростью. Скорости остальных, промежуточных слоев, плавно меняются (см. рис. 4.4).

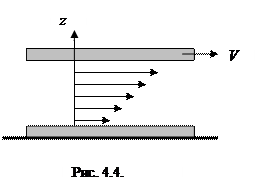Итак, существует зависимость скорости слоев жидкости (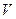) от . Производная называется градиентом скорости. В линейном приближении , где и 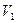- скорости слоев жидкости, находящихся на расстоянии 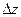друг от друга. Ньютон установил, что сила вязкого трения, препятствующая взаимному движению слоев, пропорциональна градиенту скорости и площади их соприкосновения ():

,

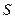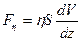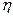- коэффициент вязкости. .

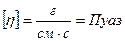Величина 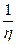называется коэффициентом текучести.

Физически, коэффициент вязкости показывает, какую силу надо приложить к слою жидкости толщиною в единицу длины и площадью в единицу площади, чтобы верхняя поверхность слоя двигалась относительно нижней со скоростью, равной единице скорости.

Течение вязкой жидкости может быть двух типов: ламинарным и турбулентным.

Ламинарное течение реализуется при малых скоростях и характеризуется тем, что в каждой точке потока все его параметры либо постоянны во времени, либо меняются по некоторому закону, заданному извне. Параметры потока в каждой точке воспроизводимы. Слои жидкости не перемешиваются друг с другом.

Турбулентное течение наступает, когда скорость течения превышает некоторый уровень. В этом случае параметры потока меняются во времени по случайному закону.

Ламинарное течениехарактеризуется плавным нарастанием скорости движения слоев жидкости по мере удаления от стенки. Распределение скоростей при ламинарном течении жидкости в трубе (см. рис. 4.5) определяется уравнением

,

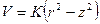где - расстояние от центра трубы, радиуса ,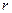

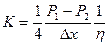- коэффициент пропорциональности.

Выражение для средней скорости движения жидкости (газа) в трубе эмпирически нашел Пузель (Формула Пуазеля).

.

Т.к. количество жидкости, прошедшей за 1 секунду через сечение 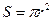определяется выражением 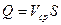, формула Пуазеля может быть представлена в виде:

.

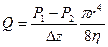При турбулентном движении профиль скоростей более ровный, что является следствием их перемешивания (см. рис. 4.6).

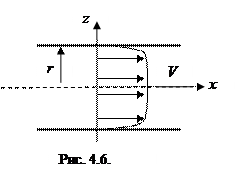Опыт показывает, что распределение скорости слоев жидкости по радиусу трубы имеет вид:

,

где 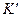- численный коэффициент.

Выражение для средней скорости движения жидкости при турбулентном течении имеет вид (формула Шези):

,

где - коэффициент сопротивления течению жидкости.

Если этот коэффициент определить для ламинарного течения как 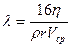, то формула Шези сводится к формуле Пуазеля. В этом смысле формула Шези является более универсальной.

4.4. Сопротивление движению тел в жидкостях

Выше были представлены простейшие законы движения жидкости (газа). Теперь рассмотрим особенности движения тел в жидкостях (газах).

Как установил Стокс, на тело шарообразной формы, движущееся с небольшой скоростью в жидкости, действует сила сопротивления, равная

,

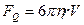где 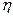- коэффициент вязкости,

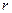- радиус шарика,

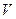- его скорость движения.

Эта формула часто используется для расчета стационарной скорости падения шарообразного тела в вязкой среде (). Определим эту скорость. При равномерном движении тел все действующие на него силы уравновешивают друг друга. Для рассматриваемого случая

,

где 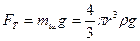– сила тяжести,

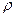- плотность материала шарика,

- сила вязкого трения Стокса,

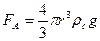- сила Архимеда,

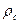- плотность среды.

Решение этого уравнения относительно имеет вид:

.

Более детальное рассмотрение этой задачи, позволяет найти динамику движения тела сферической формы в вязкой среде. В соответствии со вторым законом Ньютона, предполагая, что движение происходит в направлении оси 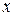, запишем:

.

Это уравнение может быть преобразовано к виду:

,

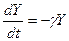где ,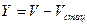

,

.

Решением выше представленного уравнения является:

.

Величина постоянной интегрирования находится из условия, что в начальный момент времени скорость тела была равной 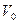, поэтому .

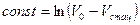В результате получаем:

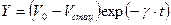
или

.

Анализ представленного решения показывает, что в зависимости от начальных условий, соотношения плотностей материалов шарика и среды движение тела будет различным. На рис. 4.7 представлен характер изменения скорости шарообразного тела, плотность которого выше плотности среды, для двух значений начальной скорости.

При больших скоростях движения тел в жидкостях или газах возникают завихрения, энергия затрачивается на их образование при этом сила сопротивления становится пропорциональной и площади сечения тела 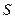, перпендикулярной скорости движения. Для этого случая Ньютоном была получена формула для силы трения, которая имеет вид:

,

где 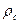- плотность среды,

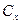- коэффициент лобового сопротивления, который зависит от формы тела, определяющей характер вихрей:

- квадратная пластинка, перпендикулярная потоку газа (жидкости). ,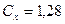

- диск, перпендикулярный потоку газа (жидкости). ,

- шар, ,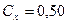

- сигарообразное тело (длина = 4 диаметрам). .

Физический смысл формулы Ньютона состоит в том, что тело, при своем движении, оттесняет за 1 секунду массу жидкости (газа), равную . Скорость, сообщаемая телом частицам оттесненной среды, в среднем равна скорости самого тела, поэтому, количество движения, теряемое телом за одну секунду, будет равно . Эта величина определяет возникающую силу сопротивления движению, силу, обусловленную инерционными свойствами частиц среды.

Дата добавления: 2014-01-05