Построение проекций точек принадлежащих поверхности

Пересечение поверхностей плоскостью и прямой линией. развертки

Нелинейчатые поверхности

Примером нелинейчатых поверхностей являются: циклические, каналовые, трубчатые поверхности, поверхности вращения.

В общем случае сечениями поверхностей многогранников являются ломаные линии, сечениями кривых поверхностей – кривые линии, проекции которых строятся по проекциям ряда точек принадлежащим как поверхности, так и секущей плоскости. При этом точки, образующие линию пересечения, разделяются на опорные и промежуточные. Опорными точками являются: точки, принадлежащие участвующим в пересечении ребрам многогранника; точки, в которых линия пересечения пересекает линию видимого контура поверхности; экстремальные точки – самая верхняя и самая нижняя, самая близкая и самая дальняя относительно той или иной плоскости проекций. Если секущая плоскость занимает частное, например, проецирующее положение, и одна проекция точек линии пересечения получается без всяких построений, то для определения другой проекции нужно исходить из принадлежности точек данной поверхности.

Так как многогранная поверхность представляет собой совокупность отдельных граней – плоскостей, то построения принадлежащих поверхности точек сводится к построению точек принадлежащих плоскости.

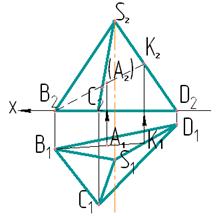
Рис. 8.1.

В плоскости SBD (рис. 8.1) через точку А проводится прямая ВК принадлежащая этой плоскости, так как имеет с ней на чертеже две общие точки (точку А и точку К, лежащую на стороне SD). Тогда на комплексном чертеже ее горизонтальная проекция В₁К₁ пройдет через А₁. Фронтальная проекция В₂К₂, а затем и фронтальная проекция точки А₂ получится построением с использованием ЛПС. Так как на фронтальной плоскости проекций грань пирамиды SBD невидима, то проекция прямой В₂К₂ проводится штриховой линией.

Для линейчатых поверхностей вращения построение принадлежащих им точек и их проекций, можно выполнить при помощи параллели или прямолинейной образующей, проходящих через эти точки.

Рис. 8.2.

Построение горизонтальных проекций А₁, В₁ точек А и В, принадлежащих поверхности прямого кругового цилиндра, по заданным фронтальным проекциям А₂ и В₂ начинаем с анализа расположений проекций точек на фронтальной плоскости проекций П₂ (рис. 8.2). Точка А находится на видимой части поверхности цилиндра, а точка В – на невидимой, так как ее фронтальная проекция В₂ заключена в круглые скобки.

Учитывая горизонтально проецирующее положение цилиндра (ось вращения i ^ П₁), можно сделать вывод, что горизонтальные проекции любых точек лежащих на боковой поверхности цилиндра будут расположены на его горизонтальной проекции (на окружности).

Рис. 8.3.

Покажем построение горизонтальной проекций А₁, В₁ точки А, В принадлежащей поверхности прямого кругового конуса, по заданной фронтальной проекции А₂ и В₂ (рис. 8.3).

Проводя анализ расположения проекции точки А на фронтальной плоскости проекций П₂, можно сделать вывод, что точка А находится на видимой части поверхности конуса по отношению к П₂, так как фронтальная проекция А₂ точки не заключена в круглые скобки.

Для решения задачи на П₂ через фронтальную проекцию S₂ вершины конуса S и А₂ проводится фронтальная проекция m₂ образующей m. Затем по ЛПС определяется положение горизонтальной проекции образующей m₁ и на ней – искомая проекция точки А₁. Профильную проекцию точки А₃ получают построениями с использованием ЛПС.

Если была бы задана горизонтальная проекция А₁ точки А и требовалось построить ее фронтальную А₂ проекцию, то построения проводились бы в обратном порядке.

Проводя анализ расположения проекции точки В на фронтальной плоскости проекций П₂, можно сделать вывод, что точка В₂ находится на невидимой части поверхности конуса по отношению к П₂, так как фронтальная проекция В₂ точки заключена в круглые скобки.

Для решения задачи, через фронтальную проекцию В₂ проводится фронтальная проекция n₂ параллели n (в виде отрезка, перпендикулярного фронтальной проекции i₂ оси вращения i). Длина этого отрезка равна натуральной величине диаметра окружности параллели. Используя радиус этой параллели (ось вращения делит отрезок-диаметр пополам) строится на П₁ горизонтальная проекция параллели n₁ (в виде окружности) и по ЛПС определяется искомое положение В₁. Профильную проекцию точки В₃ получают построениями с использованием ЛПС.

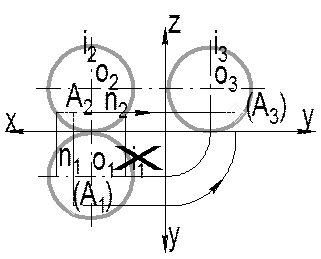
Рис. 8.4.

Рассмотрим построение горизонтальной проекции А₁, точки А, принадлежащей сферической поверхности с центром в точке О (которая проецируется на все три плоскости в окружности, диаметры которых равны диаметру сферы), по заданной фронтальной проекции А₂ (рис. 8.4). Точка А на фронтальной плоскости проекций П₂ находится на видимой части поверхности сферы относительно главной меридианальной плоскости поверхности, так как фронтальная проекция А₂ точки не заключена в круглые скобки. С другой стороны, ее фронтальная проекция А₂ располагается ниже плоскости экватора сферы, т.е. находится на невидимой по отношению к П₁ части сферической поверхности и, следовательно, ее горизонтальная проекция А₁ будет невидимой.

Для решения задачи, на П₂ через фронтальную проекцию А₂ проводится фронтальная проекция n₂ параллели n (в виде отрезка, перпендикулярного фронтальной проекции i₂ оси вращения i). Длина этого отрезка равна натуральной величине диаметра окружности параллели. Используя радиус этой параллели (ось вращения делит отрезок-диаметр пополам) строится на П₁ горизонтальная проекция параллели n₁ (в виде окружности) и по ЛПС определяется искомое положение А₁. Профильную проекцию точки А₃ получают построениями с использованием ЛПС.

8.2. Пересечение гранной поверхности плоскостью,построение проекций и натуральной величины сечения. Построение развертки.

В общем случае в сечении гранной поверхности плоскостью получается многоугольник. Вершинами многоугольника являются точки пересечения ребер многогранника с секущей плоскостью, а сторонами – отрезки прямых пересечения граней многогранника с секущей плоскостью. Т.е. построения сечения многогранника плоскостью можно свести к построениям точек пересечения прямой (ребер многогранника) с плоскостью или к построениям линии пересечения двух плоскостей (грани многогранника и секущей плоскости).

Рассмотрим сечение правильной пирамиды SABC фронтально проецирующей плоскостью Р (Р₁, Р₂) (рис. 8.5). Вершины сечения, точки 1, 2, 3 представляют собой точки пересечения ребер пирамиды SA, SB, SC с секущей плоскостью Р, фронтальный след Р₂ которой является собирательным. Следовательно, положение фронтальных проекций 1₂, 2₂, 3₂ точек сечения выявляется без всяких дополнительных построений. Положение горизонтальных 1₁, 2₁, 3₁ и профильных 1₃, 2₃, 3₃ проекций точек сечения определяется на основании их принадлежности соответствующим прямым (ребрам) – SA, SB, SC с использованием ЛПС. Полученные проекции вершин сечения попарно соединяют отрезками прямых c учетом их видимости относительно П₁ и П₂.

Рис. 8.5.

Найдем натуральную величину сечения пирамиды фронтально проецирующей плоскостью Р (Р₁, Р₂) методом совмещения.

Совмещение - частный случай вращения геометрических элементов вокруг горизонтали или фронтали, когда осью вращения является горизонтальный или фронтальный следы плоскости.

При совмещении с плоскостью проекций геометрическая фигура отобразиться на ней в натуральную величину. Натуральная величина сечения (Δ1⁰2⁰3⁰) определена методом совмещения секущей плоскости Р (Р₁, Р₂) с горизонтальной плоскостью проекций П₁ вращением ее вокруг оси i (i º Р₁) (рис. 8.5).

Разверткой поверхности какого-либо тела называется фигура, полученная совмещением поверхности этого тела с плоскостью чертежа. Между поверхностью и ее разверткой существует точечное соответствие, т.е. конкретной точке лежащей на поверхности соответствует единственная точка на развертке, и наоборот.

Поверхность называется развертывающейся, если она как гибкая, но нерастяжимая и несжимаемая пленка может быть совмещена с плоскостью без образования складок и разрывов. Многогранные поверхности и кривые линейчатые поверхности с ребром возврата обладают свойством развертываемости, а линейчатые косые и нелинейчатые поверхности этим свойством не обладают.

Развертка гранной поверхности представляет собой плоскую фигуру, получаемую при совмещении всех ее граней с плоскостью. Следовательно, для построения развертки требуется определение натуральных величин всех ее ребер (боковых и сторон основания).

Рис. 8.6

Так как боковыми гранями любой пирамиды являются треугольники, то для их построения по трем сторонам необходимо сначала определить натуральные величины боковых ребер и сторон основания пирамиды. Но учитывая то, что, в нашем случае, пирамида является правильной (все ее грани равны) и стороны ее основания проецируются на плоскость П₁ в натуральную величину, так как занимают положение горизонтального уровня (А₂В₂, В₂С₂, А₂С₂ // оси ох), эти определения проводить не нужно. Сразу строят четыре одинаковых, равносторонних треугольника (рис. 8.6). А вот для определения на развертке точек 1, 2, 3 линии сечения потребуется определение натуральной величины отрезков [ S1 ], [ S2 ], [ S3 ]. Для определения натуральной величины этих отрезков можно воспользоваться способом прямоугольного треугольника или способом вращения.

Натуральные величины отрезков [ S1 ], [ S3 ] определены способом вращения вокруг оси, проходящей через вершину S и перпендикулярной плоскости П₂ до положения горизонтального уровня (рис. 8.6). Отрезок [ S2 ] проецируется в натуральную величину на П₃, так как занимает положение профильного уровня (S₂2₂ и S₁2₁ ^ оси ох).

При необходимости построения полной развертки усеченной вышерассмотренной пирамиды SABC производят дополнительные построения (рис. 8.6) фигуры сечения (Δ123) в натуральную величину.

Для построения на развертке пирамиды произвольной точки D, принадлежащей грани SBC (рис. 8.5), сначала строят прямую [ S4 ], принадлежащую ΔSBC и проходящую через точку D (D₁ Є S₁4₁, D₂ Є S₂4₂). Затем эту прямую [ S4 ] строят на развертке и точку D на ней (рис. 8.6), откладывая соответственно натуральные величины отрезков [ S4 ] и [ SD ].

8.3. Пересечение кривой поверхности плоскостью,построение проекций и натуральной величины сечения. Построение развертки.

Для построения линии пересечения кривой поверхности с плоскостью в общем случае используют вспомогательные секущие плоскости. Точки искомой линии определяются в пересечении линий, по которым вспомогательная секущая плоскость пересекает поверхность и плоскость. Поэтому при построении линии пересечения необходимо знать, что может иметь в сечении та или иная кривая поверхность.

Дата добавления: 2014-01-05