При параллельном соединением элементов по надежности, надежность системы может быть повышена путем увеличения надежности каждого элемента и путем увеличения их числа

При параллельном соединением элементов по надежности, надежность системы зависит от уровня надежности каждого элемента и от их числа. С уменьшением надежности элементов и уменьшении их числа надежность системы уменьшается.

3. ПРЕОБРАЗОВАНИЕ «ТРЕУГОЛЬНИК - ЗВЕЗДА» И «ЗВЕЗДА - ТРЕУГОЛЬНИК»

В ряде случаев системы электроснабжения имеют более сложные структурные схемы по надежности, чем параллельно-последовательные. В этом случае перед определением количественных характеристик надежности необходимо сложную структуру преобразовать в эквивалентную ей параллельно-последовательную. Такое преобразование выполняется на основе преобразований «треугольник – звезда» и «звезда – треугольник».

Суть преобразований заключается в том, что схема сложной конфигурации заменяется схемой более простой конфигурации. При этом характеристики новой схемы должны быть такими, чтобы показатели надежности остались прежними.

Рассмотрим преобразование «треугольник – звезда» (рисунок 1).

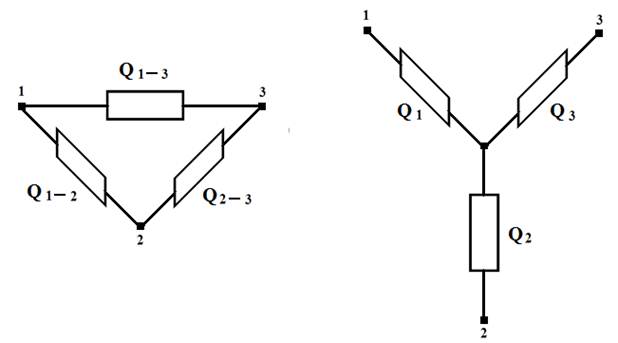
а) «треугольник» б) «звезда»

Рисунок 1. Сложные схемы по надежности: а) «треугольник»; б) «звезда»

Вероятность безотказной работы цепи 1-2 выразим поочередно через вероятности отказа элементов звезды и треугольника:

- для звезды: Р_1-2 = (1 – Q₁)·(1 – Q₂);

- для треугольника: Р_1-2 = 1 – Q_1-2·Q_1-3-2,

где Q_1-3-2 – вероятность отказа цепи 1-3-2, которая определяется как:

Q_1-3-2 = 1 - (1 – Q_1-3)·(1 – Q_2-3).

Тогда:

Р_1-2 = 1 – Q_1-2·Q_1-3-2 = 1 – Q_1-2 ·{1 - (1 – Q_1-3)·(1 – Q_2-3)}.

Приравняем вероятности безотказной работы Р_1-2 для звезды и треугольника:

(1 – Q₁)·(1 – Q₂) = 1 – Q_1-2 ·{1 - (1 – Q_1-3)·(1 – Q_2-3)}.

После раскрытия скобок и группировки величин получим:

Q₁+ Q₂ - Q₁·Q₂ = Q_1-2· (Q_2-3 + Q_3-1 – Q_2-3 · Q_3-1).

Аналогично для цепи 2-3:

Q₂+ Q₃ – Q₂·Q₃ = Q_2-3· (Q_1-3 + Q_1-2 – Q_3-1 · Q_1-2).

Аналогично для цепи 3-1:

Q₃+ Q₁ – Q₃·Q₁ = Q_3-1· (Q_1-2 + Q_2-3 – Q_1-2 · Q_2-3).

Ввиду малости можно пренебречь произведениями величин вероятностей отказов вида Q₁·Q₂, Q₂·Q₃ и Q₃·Q₁, а также произведениями величин Q_1-2· Q_2-3 · Q_3-1. Тогда системы уравнений значительно упростятся. Решая упрощенные системы уравнений получим:

- для преобразования «треугольник – звезда»:

Q₁ = Q_1-2· Q_3-1;

Q₂ = Q_2-3· Q_1-2;

Q₃ = Q_3-1· Q_2-3.

- для преобразования «треугольник – звезда»:

Q_1-2 = (Q₁· Q₂ /Q₃)^0,5;

Q_2-3 = (Q₂· Q₃ /Q₁)^0,5;

Q_3-1 = (Q₃ · Q₁ /Q₂)^0,5.

Дата добавления: 2014-01-05