Характеристики линейного звена

Для количественного описания свойств линейного звена в за­висимости от постановки задачи, пользуются следующими взаим­но связанными его характеристиками: комплексным коэффици­ентом усиления; передаточной функцией; переходной функцией; весовой функцией.

Рассмотрим определение каждой из перечисленных характе­ристик.

Комплексным коэффициентом усиления звена называется отношение комплексной амплитуды сигнала на вы­ходе к комплексной амплитуде сигнала на входе при подаче на вход синусоидального воздействия.

Из уравнения (1.4.9) комплексный коэффициент линейного звена определяется как

(1.5.1)

Полную характеристику звена дает изменение комплексного коэффициента звена при изменении частоты от нуля до беско­нечности.

Геометрическое место конца вектора комплексного коэффи­циента усиления звена при изменении частоты от нуля до беско­нечности называется частотным годографом коэффициента уси­ления или комплексной частотной характеристикой звена. Иног­да его называют также амплитудно-фазовой характеристикой звена.

Комплексный коэффициент усиления звена может быть изме­рен экспериментально, если на вход звена подать синусоидаль­ное напряжение определенной амплитуды и частоты, а на выхо­де измерить амплитуду и фазу сигнала. Так, например, если

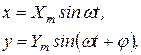
то комплексная амплитуда входного сигнала 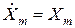, а комплексная амплитуда выходного сигнала . Таким образом,

(1.5.2)

Если на вход системы подать единичный импульс, частотный спектр которого равен единице, то частотный спектр выходного сиг­нала совпадает с зависимостью комплексного коэффициента усиле­ния от частоты. Действительно, в этом случае по формуле (1.4.9)

и, следовательно, комплексную частотную характери­стику звена можно определить как частотный спектр выходного сигнала при подаче на вход звена единичного импульса.

Такое определение носит чисто теоретический характер, так как в практических условиях реализация сиг­нала в виде единичного импульса невозможна.

Пример годографа комплексного коэффициента усиления звена (комплексной частотной характеристики) показан на рисунке 1.5.1, а. В реальных звеньях обычно для дифференциального уравнения и в выражении (1.5.1) порядок числителя меньше порядка знаменателя. На годографе это выражается тем, что при значение 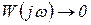. Вместо частотного годографа часто задают частотные зависимости амплитуды 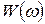и фазы (рисунок 1.5.1, б и в), понимая под амплитудой её значение на выходе при амплитуде синусоидального сигнала на входе, равном единице, или модуль коэффициента усиления.

Рисунок 1.5.1 – Амплитудно-фазовая (а), амплитудно-частотная (б) и
фазочастотная (в) характеристики звена

Передаточной функцией звена называется отношение изображения сигнала на выходе к изображению сигнала на входе при нуле­вых начальных условиях.

Согласно (1.7), передаточная функция определяется как

(1.5.3)

Переход от передаточной функции к комплексному коэф­фициенту усиления осуществляется путем замены p на .

Если известны — полюсы и 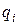— нули функции , соответствующие корням уравнений и , то выражение (1.5.3) можно записать как

(1.5.4)

Предполагается, что многочлены и 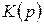не имеют общих корней и дробь (1.5.4) не может быть сокращена.

С помощью разложения функции на элементарные дроби формула (1.5.4) может быть преобразована

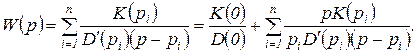(1.5.5)

Здесь предполагается, что функция не имеет кратных полюсов и что .

Переходной функцией звена называется сигнал на выходе звена при подаче на его вход единичного скачка 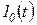. В этом случае изображение по Лапласу входного сигнала и, согласно (1.5.3), изображение выходного сигнала

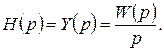(1.5.6)

Переходя от изображения к оригиналу, получаем

(1.5.7)

Переходная функция однозначно связана с передаточной функцией звена.

Выражая с помощью (1.5.5) и переходя от изобра­жения к оригиналу, получаем

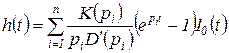(1.5.8)

или

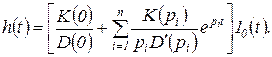(1.5.9)

Установившаяся (вынужденная) составляющая переходной функции

(1.5.10)

характеризует статические свойства звена.

Переходная (свободная) составляющая определяется как разность

(1.5.11)

Весовой, или импульсной, переходной фун­кцией 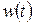называется сигнал на выходе звена при подаче на его вход единичного импульса . В этом случае изображение по Лапласу входного сигнала , а изображе­ние выходного сигнала совпадает с передаточной функцией

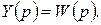(1.5.12)

Переходя от изображения к оригиналу, для весовой функции получаем

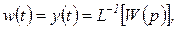(1.5.13)

т.е. весовая функция является оригиналом передаточ­ной функции. Так как изображение переходной функции отличается от передаточной функции только множителем р, то

(1.5.14)

Таким образом, зная переходную функцию, всегда можно найти весовую функцию звена. Для и , выражае­мых формулами (1.5.3) и (1.5.8), получаем

(1.5.15)

Рассмотренные четыре вида характеристик линейных звеньев однозначно связаны друг с другом и, зная одну из них, всегда можно найти любую другую.

Дата добавления: 2014-01-05