Запас и перечень

Вес функции; вес класса эквивалентности

Функции и классы.

Пусть D и R – конечные множества. Рассмотрим функции, определенные на D, со значениями в R; другими словами, рассмотрим отображения D в R. Множество всех таких функций обозначим через R^D. Число элементов в множестве R^D равно ½R½^½D½, поскольку если мы хотим построить функцию f, то мы имеем для каждого элемента dÎD ½R½возможностей выбрать f(d), и эти выборы независимы.

Далее предположим, что нам дана группа G множества D. Эта группа вводит отношение эквивалентности в R^D: две функции f₁ и f₂ (обе из R^D) называют эквивалентными (обозначим f₁~f₂), если существует элемент gÎG, такой, что

f₁(gd)= f₂(d) для всех dÎD. (8)

Соотношение (8) может быть кратко записано так: f₁g= f₂, ибо f₁g обозначает сложное отображение “сначала g потом f₁”. Легко установить обычные условия эквивалентности: 1) f~f; 2) если f₁~f₂, то f₂~f₁; 3) если f₁~f₂ и f₂~f₃, то f₁~f₃. Первое условие следует из того, что тождественная подстановка принадлежит G; второе условие следует из того, что если gÎG, то обратная подстановка g^-1 принадлежит G; и третье – из того, что если g₁ÎG, g₂ÎG, то g₁g₂ÎG.

Таким образом, ~ есть отношение эквивалентности, с помощью которого R^D разбивается на классы эквивалентности.

Пример 8. Пусть D – множество, состоящее из всех шести граней куба, и пусть G – группа всех подстановок D, которые могут быть получены вращениями куба (см. пример 3). Пусть R состоит из двух слов: красный и белый. Элемент fÎR^D может быть рассмотрен как способ окрашивания куба (так что каждая грань красная, либо белая). Это может быть сделано 2⁶ способами. Если два таких куба, расположенных параллельно окрашены различно, то может случиться, что один из них можно повернуть так, что кубы перестанут казаться различными. В этом случае они принадлежат одному классу эквивалентности.

В нашем примере десять классов эквивалентности, которые могут быть описаны следующим образом (в скобках – число функций в каждом классе эквивалентности): (а) все грани красные (1); (б) пять граней красные, одна белая (6); (в) две противоположные грани белые, остальные четыре красные (3); (г) две смежные грани белые, остальные четыре красные (12); (д) три грани, имеющие общую вершину, красные, остальные белые (8); (е) две противоположные и одна из оставшихся красные, три остальные белые (12); (ж), (з), (и), (к) получаются из (г), (в), (б), (а) заменой слов ‘красный’ на ‘белый’. В качеств примера заметим, что

1+6+3+12+8+12+12+3+6+1=2⁶.

Пример 9. Пусть D – множество, состоящее из трех элементов {1,2,3}, и пусть G – симметрическая группа всех перестановок из D и пусть R состоит из двух элементов x и y. В этом случае восемь функций, а классов эквивалентности четыре. Классы эквивалентности можно обозначить символами x³, x²y, xy², у³ соответственно. Например, x²y представляет класс отображений f, таких, что два из значений f(1), f(2), f(3) равны x и одно у. Класс эквивалентности x³ состоит только из одной функции, которая определена так:

f(1)=f(2)=f(3)=x.

Полезно рассмотреть также x и y как независимые переменные и поставить в соответствие каждой функции f произведение f(1)f(2)f(3), которое не зависит от порядка сомножителей. Другими словами, так как симметрическая группа дана, то говорить, что две функции f₁ и f₂ эквивалентны, – это то же, что сказать, что произведение f₁(1)f₁(2)f₁(3) и f₂(1)f₂(2)f₂(3) тождественны. Поэтому классы эквивалентности характеризуются возможными значениями произведений, а именно одночленами x³, x²y, xy², у³.

Опять возьмем конечные множества D и R и группу G постановок множества D. Каждому элементу множества R придадим вес. Этот вес может быть числом, или переменной, или вообще элементом коммутативного кольца, состоящего из рациональных чисел. Таким образом, мы можем образовывать суммы и произведения весов, произведения весов на рациональные числа, и эти операции удовлетворяют обычным законам ассоциативности, коммутативности и дистрибутивности. Вес, придаваемый элементу rÎR, обозначим через w(r).

После того как выбраны эти веса мы можем определить вес W(f) функции fÎR^D произведение

W(f)=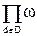[f(d)]. (9)

Если f₁ и f₂ принадлежат одному классу эквивалентности, то они имеют одинаковый вес. Это следует из того факта, что если f₁g=f₂, gÎG, то

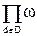[f₁(d)]= 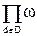[f₁(gd)]= 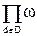[f₂(d)],

поскольку первое и второе произведение имеют одни и те же сомножители, разве что в другом порядке, и в силу коммутативности произведения весов.

Так как все функции, принадлежащие одному и тому же классу эквивалентности, имеют одинаковый вес, мы можем определить в качестве веса класса эквивалентности это общее значение. Таким образом, если F обозначает класс эквивалентности, обозначим вес его через W(F); использование символа W как для веса класс вряд ли вызовет путаницу.

Пример 10. Рассмотрим случай окрашивания куба из примера 8 и образуем кольцо всех многочленов от двух переменных x и y с рациональными коэффициентами. Множество R состоит из элементов красный и белый, которым мы придадим в качестве весов значения x и y соответственно. Десять классов эквивалентности (а), …, (к) имеют теперь веса

x⁶, x⁵y, x⁴y², x⁴y², x³y³, x³y³, x²y⁴, x²y⁴, xy⁵, у⁶

соответственно. Отсюда можно видеть, что различные классы эквивалентности не обязаны иметь различные веса.

Пример 11. В примере 9 множество R имело два элемента x и y. Если считать x и y переменными, то нет причин, запрещающих дать элементу x вес x, а элементу y – вес y. Теперь символы x³, x²y, xy², у³ действительно стали весами классов. В этом случае вес характеризует класс: различные классы обладают различными весами.

Пример 12. Если взять w(r)=1 для всех rÎR, то мы будем иметь W(f)=1 для всех функций W(F)=1 для всех классов эквивалентности.

Как и раньше, имеем множества D и R, и каждый элемент rÎR обладает весом. Считая R множеством, из которого выбираем значения для функций, назовем R запасом. Так как веса можно складывать, то существует сумма весов; эта сумма называется производящей функцией запаса или перечнем множества R:

Перечень R=. (10)

Пример 13. Терминология наводит на мысль, что перечень дает достаточно точное описание элементов R, однако это верно лишь отчасти. Пусть R – множество, содержащее три коробки мыла (назовем их м₁, м₂, м₃), два пакета чая (назовем ч₁, ч₂,) и четыре бутылки вина (в₁, в₂, в₃, в₄). Если мы возьмем девять переменных м ₁, м ₂, м ₃, ч ₁, ч ₂, в ₁, в ₂, в ₃, в ₄ и придадим элементу м₁ вес м ₁ и т. д., то перечень будет иметь вид

м ₁ + м ₂ + м ₃ + ч ₁ + ч ₂ + в ₁ + в ₂ + в ₃+ в ₄,

и значение суммы даст полную информацию о запасе. Лавочник обычно применяет более простую систему, так как он не интересуется мелкими различиями между полностью эквивалентными предметами. Он обозначает символами м, ч, в абстрактные понятия ‘коробка мыла’. ‘пакет чая’, ‘бутылка вина’. Затем он придаст всем элементам м₁, м₂, м₃ один вес м; каждому из ч₁, и ч₂ – один вес ч, в₁ и в₂ – вес в, элементам в₃ и в₄ – вес ½ в (так как в₃ и в₄ пол-бутылки, а разница между ними самими к делу не относится). Его перечень имеет вид 3 м +2 ч +3 в. Иногда, впрочем, лавочник, или ревизор интерисуется значением запаса в долларах. Если он оценивает коробку мыла в 3, пакет чая в 1, бутылку вина в 2, а пол-бутылки в 1 доллар, то перечень примет вид 9+2+4+2=17. Теперь перечень просто число; он не дает информации о том, из чего состоит запас, кроме того факта, что его общая стоимость равна 17долларам. В конце концов у лавочника есть еще возможность обучить своего клерка считать: придавая каждому предмету перечня вес 1, можно получить значение перечня, равное общему числу предметов, т.е. 9.

Дата добавления: 2014-01-06