
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Пример
|
|
|
|
f(x 1, x 2, x 3 ) = .
.
f(x 1, x 2, x 3 ) =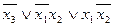 .
.
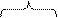  x 2 x 2 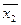
| Четыре единицы, находящиеся в первой и последней колонках, можно накрыть перемен- | ||||||
  x 1 x 1
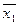
| ной 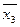 , а две остальные объединить с единицами, расположенными в левой нижней и правой , а две остальные объединить с единицами, расположенными в левой нижней и правой
| ||||||
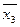 x 3
x 3 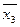 верхней клетках диаграммы (склеивание по x 3).
верхней клетках диаграммы (склеивание по x 3).
Данная функция имеет единственную минимальную форму, так как при любом другом способе объединения единиц количество букв в ДНФ увеличивается.
Пример. Найти минимальные ДНФ и КНФ функции
f(x 1, x 2, x 3 ) = 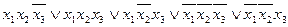 .
.
      x 2 x 2 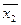 x 2 x 2 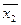
| ||||||||||
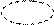 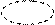 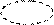 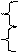    x 1 x 1
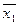
| x 1
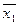
| |||||||||
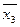 x 3
x 3 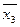
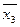 x 3
x 3 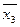
f(x 1, x 2, x 3 ) = x 1 x 2Ú x 1 x 3Ú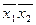 f(x 1, x 2, x 3 ) = x 1 x 2Ú
f(x 1, x 2, x 3 ) = x 1 x 2Ú 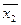 x 3Ú
x 3Ú 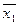
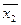
Для получения минимальной КНФ следует объединить нули переключательной функции: две конституенты нуля соответствуют клеткам, объединенным пунктиром, склеиваются по x 3 и представляются импликантой x 1Ú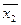 , а оставшийся нуль – конституентой
, а оставшийся нуль – конституентой 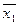 Ú x 2Ú x 3. Поэтому минимальная КНФ будет иметь вид:
Ú x 2Ú x 3. Поэтому минимальная КНФ будет иметь вид:
f (x 1, x 2, x 3) = (x 1Ú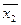 )(
)( Ú x 2Ú x 3).
Ú x 2Ú x 3).
Минимальная КНФ имеет меньше букв, чем минимальная ДНФ.
Пример. Найти минимальную ДНФ.
f(x 1, x 2, x 3 ) = .
.
    x 2 x 2 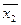
|
Единственная минимальная ДНФ имеет
вид 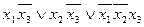
| |||
   x 1 x 1
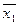
| ||||
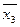 x 3
x 3 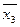
Пример. Найти минимальную ДНФ.
f(x 1, x 2, x 3 ) =  .
.
    x 2 x 2 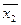
| f(x 1, x 2, x 3 ) = x 2 x 3Ú x 1 x 3Ú x 1 x 2; f(x 1, x 2, x 3 ) = x 1 x 3Ú x 1 x 2Ú x 2 x 3; | |||
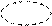  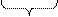  x 1 x 1
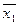
| ||||
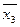 x 3
x 3 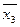 При других способах объединения консти-
При других способах объединения консти-
туент число логических слагаемых в ДНФ
будет больше трех.
Пример. Найти минимальную ДНФ функции
|
|
|
f(x 1, x 2, x 3 ) =  .
.
   x 2 x 2 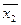
| В диаграмме Вейча данной функции нет ни одной пары единиц, расположенных в соседних клетках, и поэтому заданная СДНФ совпадает с минимальной. | |||
 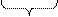  x 1 x 1
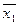
| ||||
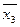 x 3
x 3 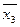
Диаграмма Вейча для функции четырех аргументов представляет собой квадрат, разделенный на 16 клеток.
|
 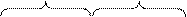   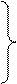  x 1
x 1
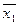
| x 2 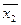
|
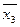 x 3
x 3
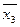
| |
 x 4 x 4 
|
Первую и последнюю колонки диаграммы, а также верхнюю и нижнюю строки следует считать соседними. Поэтому диаграмму Вейча для функций четырех аргументов следует представлять нанесенной на поверхность тора.
Пример.

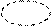  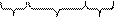  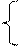  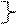 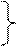 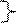
x 1
| x 2 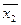
|
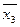 x 3
x 3
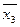
| ||
 x 4 x 4 
|
Диаграмма Вейча для функции пяти аргументов имеет следующий вид:
 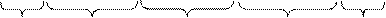     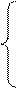 x 1
x 1
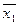
| x 2 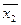 x 5
x 5  x 5 x 5
|
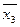  x 3
x 3
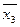
| |||||
 x 4 x 4  x 4 x 4 
|
Одной букве в этом случае соответствуют шестнадцать единиц, расположенных в смежных клетках; произведение двух букв – восемь единиц, трех букв – четыре, четырех – две и пяти – одна единица.
Следует помнить, что для букв 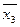 , x 4,
, x 4,  и x 5 "соседние" клетки оказываются разнесенными.
и x 5 "соседние" клетки оказываются разнесенными.
|
|
|
Аналогично строится диаграмма Вейча и для переключательных функций большего числа аргументов. Однако с увеличением числа аргументов работа с диаграммами затрудняется, т.к. теряется геометрический смысл "соседних" клеток.
2.6. Второй метод получения минимальных КНФ
Этот метод полностью опирается на преобразования дизъюнктивных форм переключательных функций. Алгоритм заключается в следующем.
1. Записывают дизъюнкцию всех конституент единицы, которые не входят в СДНФ заданной функции.
Если функция задана таблицей, то в эту форму войдут конституенты единицы, соответствующие наборам аргументов, на которых функция равна нулю. Если функция задана аналитически, то вначале находят ее совершенную ДНФ, а затем записывают дизъюнкцию всех конституент, которые не вошли в эту функцию. Можно показать, что полученная таким образом форма будет совершенной дизъюнктивной нормальной формой заданной функции, взятой с отрицанием.
2. Находят минимальные ДНФ по рассмотренным алгоритмам.
3. От полученных минимальных форм берут отрицания, и после преобразований по формулам де Моргана получают конъюнктивные формы, которые будут минимальными.
Для обоснования приведенного алгоритма получения минимальной КНФ достаточно доказать два положения.
1. Дизъюнкция всех конституент единицы, не входящих в совершенную дизъюнктивную нормальную форму данной функции f (x 1, x 2, …, xn) является отрицанием данной функции 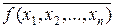 .
.
2. Преобразования по формулам де Моргана минимальной дизъюнктивной нормальной формы функции 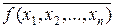 приводит к получению минимальной конъюнктивной нормальной формы функции f (x 1, x 2, …, xn).
приводит к получению минимальной конъюнктивной нормальной формы функции f (x 1, x 2, …, xn).
1. Прежде всего заметим, что дизъюнкция всех конституент единицы тождественно равна единице. Действительно, для любого набора аргументов в такой дизъюнкции найдется конституента, равная на этом наборе единице. Но если одно логическое слагаемое ДНФ равно единице, то равна единице и вся дизъюнктивная форма. Поэтому справедливы такие, например, соотношения

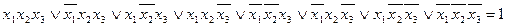
В общем виде:
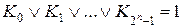 , (*)
, (*)
где n – число аргументов.
Рассмотрим некоторую ПФ, заданную в СДНФ:
 , (**)
, (**)
где m – число наборов, на которых ПФ равна единице.
|
|
|
Обозначим конституенты единицы, не входящие в последнее выражение, через  , где p = 2 n – m – число наборов, на которых функция равна нулю. Тогда на основании соотношения (*)
, где p = 2 n – m – число наборов, на которых функция равна нулю. Тогда на основании соотношения (*)
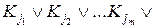

Учитывая (**), получим

Сравнивая последнее соотношение с тождеством х 1Ú 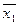 = 1, которое можно записать в форме
= 1, которое можно записать в форме
 ,
,
получим
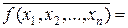
 ,
,
что и требовалось доказать.
Преобразования по формулам де Моргана не изменяют число букв в выражении для ПФ. Поэтому, если взять отрицание от минимальной ДНФ функции 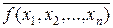 , то полученная после преобразования по формулам де Моргана конъюнктивная форма также будет минимальной, но уже для функции
, то полученная после преобразования по формулам де Моргана конъюнктивная форма также будет минимальной, но уже для функции 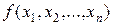 .
.
Если предположить, что эта форма не является минимальной, то существует другая конъюнктивная форма, содержащая меньшее число букв. Тогда, взяв от нее отрицание и применив формулы де Моргана, получим дизъюнктивную форму с меньшим числом букв, чем в минимальной. Это противоречит определению минимальной формы и, следовательно, предположение о том, что полученная конъюнктивная форма не является минимальной, не верно.
Пример 1. Найти минимальную конъюнктивную форму ПФ, заданной таблицей.
|
| Номер набора | ||||||||
| x 1 | ||||||||
| x 2 | ||||||||
| x 3 | ||||||||
| f (x 1, x 2, x 3) |
 .
.
2. Выполним операции склеивания и поглощения, после чего получим сокращенную ДНФ функции 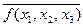 :
:
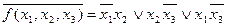 .
.
3. Испытывая импликанты, обнаружим, что вторую импликанту можно исключить (при x 2 = 1, x 3 = 0, выражение 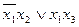 º 1), т.е. минимальная ДНФ функции
º 1), т.е. минимальная ДНФ функции 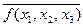 имеет вид
имеет вид
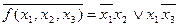 .
.
Использовав формулу де Моргана, получим минимальную КНФ заданной функции
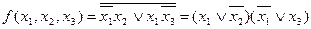 .
.
Пример 2. Найти минимальную конъюнктивную нормальную форму функции
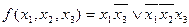 .
.
1. Находим СДНФ:
 .
.
2. Записав дизъюнкцию конституент единицы, не вошедших в предыдущее выражение, получим СДНФ функции 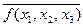 :
:
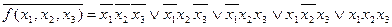 .
.
3. Сокращенная ДНФ имеет вид:
|
|
|
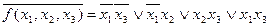 .
.
4. Находим минимальные формы функции 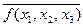 .
.
| Импли- канта | Конституента | ||||

| 
| 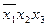
| 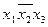
| x 1 x 2 x 3 | |
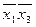
| * | * | |||
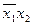
| * | * | |||
| x 2 x 3 | * | * | |||
| x 1 x 3 | * | * |
1) 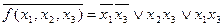 .
.
2) 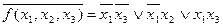 .
.
Воспользовавшись формулой де Моргана получим две минимальные КНФ:
1. f (x 1, x 2, x 3) = (x 1Ú x 3)(x 2Ú x 3)(x 1Ú x 3).
2. f (x 1, x 2, x 3) = (x 1Ú x 3)(x 1Ú x 2)(x 1Ú x 3).
2.7. Минимизация неполностью определенных переключательных функций
В ЦВМ могут использоваться комбинационные схемы, закон функционирования которых определен неполностью. В таких схемах некоторые комбинации сигналов на ее входы не подаются и являются запрещенными. Для запрещенных входных комбинаций выходные сигналы не определены, т.е. могут принимать любые значения – нуль или единицу. Поэтому при синтезе схем с неполностью заданным законом функционирования можно произвольно задать значения выходных сигналов для запрещенных комбинаций входных сигналов; нормальная работа схемы при этом не нарушается. Поэтому выходным сигналам на запрещенных комбинациях придают такие значения, при которых можно построить наиболее простую схему.
Схемы с запрещенными комбинациями выходных сигналов описываются неполностью определенными переключательными функциями, т.е. функциями, значения которых определены не на всех наборах. Например, функция заданная таблицей и диаграммой Вейча
 |
 x 1 x 1
| ||||||
 x 2 x 2
| ||||||
| x 3 | ||||||
| f (x 1, x 2, x 3) |
определена только на шести наборах. Клетки, соответствующие наборам 1,0,0; 1,1,1 остаются пустыми.
Форма представления функции f (x 1, x 2, x 3) существенно зависит от выбора ее значений на запрещенных наборах, Например, для заданной функции, выбирая ее запрещенные значения равными нулю, можно получить минимальную ДНФ в виде
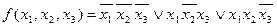
Если значения функции на запрещенных наборах принять равными единице, то форма представления упрощается
 .
.
Рассмотрим общую методику получения минимальных ДНФ неполностью определенных переключательных функций
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 246; Нарушение авторских прав?; Мы поможем в написании вашей работы!
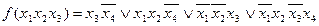 –
- это минимальная ДНФ.
–
- это минимальная ДНФ.