Статистический подход к измерению информации

Аддитивная мера

предложена в 1928 году американским ученым Хартли, второе название – мера Хартли.

Хартли впервые ввел специальное обозначение для количества информации – I и предложил следующую логарифмическую зависимость между количеством информации и мощностью исходного алфавита:

I = Llog h,

где I – количество информации, содержащейся в сообщении;

L– длина сообщения;

h – мощность исходного алфавита.

При исходном алфавите {0,1}; L = 1; h = 2 и основании логарифма, равном 2, имеем

I = 1*log₂2 = 1.

формула даёт аналитическое определение бита (BIT - BInary digiT) по Хартли: это количество информации, которое содержится в двоичной цифре.

Единицей измерения информации в аддитивной мере является бит.

В 30-х годах ХХ века американский ученый Клод Шеннон предложил связать количество информации, которое несет в себе некоторое сообщение, с вероятностью получения этого сообщения.

Вероятность p – количественная априорная (т.е. известная до проведения опыта) характеристика одного из исходов (событий) некоторого опыта.

Измеряется в пределах от 0 до 1.

Если заранее известны все исходы опыта, сумма их вероятностей равна 1, а сами исходы составляют полную группу событий.

Если все исходы могут свершиться с одинаковой долей вероятности, они называются равновероятными.

Пусть можно получить n сообщений по результатам некоторого опыта (т.е. у опыта есть n исходов), причем известны вероятности получения каждого сообщения (исхода) - pi. Тогда в соответствии с идеей Шеннона, количество информации I в сообщении i определяется по формуле:

I = -log₂ pi,

где pi – вероятность i-го сообщения (исхода).

Пример 1. Определить количество информации, содержащейся в сообщении о результате сдачи экзамена для студента-хорошиста.

Пусть I(j) – количество информации в сообщении о получении оценки j. В соответствии с формулой Шеннона имеем:

I(5) = -log₂ 0,5 = 1,

I(4) = -log₂ 0,3 = 1,74,

I(3) = -log₂ 0,1 = 3,32,

I(2) = -log₂ 0,1 = 3,32.

Таким образом, количество получаемой с сообщением информации тем больше, чем неожиданнее данное сообщение.

Формула Шеннона позволяет определять также размер двоичного эффективного кода, требуемого для представления того или иного сообщения, имеющего определенную вероятность появления.

Пример 2. Есть 4 сообщения: a, b, c, d с вероятностями, соответственно, р(a) = 0,5; р(b) = 0,25; р(c) = 0,125; р(d) = 0,125. Определить число двоичных разрядов, требуемых для кодирования каждого их четырех сообщений.

В соответствии с формулой Шеннона имеем:

I(a) = -log₂0,5 = 2=L,

I(b) = -log₂0,25 = 2=L,

I(c) = -log₂0,125 = 3=L,

I(d) = -log₂0,125 = 3=L.

Помимо информационной оценки одного сообщения, Шеннон предложил количественную информационную оценку всех сообщений, которые можно получить по результатам проведения некоторого опыта. Так, среднее количество информации Iср, получаемой со всеми n сообщениями, определяется по формуле:

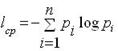
где pi – вероятность i-го сообщения.

Пример 3. Определить среднее количество информации, получаемое студентом-хорошистом, по всем результатам сдачи экзамена.

В соответствии с приведенной формулой имеем:

Iср = - (0,5*log₂0,5 + 0,3*log₂0,3 + 0,1*log₂0,1 + 0,1*log₂0,1) = 1,67.

Пример 4. Определить среднее количество информации, получаемое нерадивым студентом, по всем результатам сдачи экзамена.

В соответствии с приведенной формулой имеем:

Iср = - (0,1*log₂0,1 + 0,2*log₂0,2 + 0,4*log₂0,4 + 0,3*log₂0,3) = 1,73.

Большее количество информации, получаемое во втором случае, объясняется большей непредсказуемостью результатов: в самом деле, у хорошиста два исхода равновероятны.

Пусть у опыта два равновероятных исхода, составляющих полную группу событий, т.е. p1 = p2 = 0,5. Тогда имеем в соответствии с формулой для расчета I ср:

I ср = -(0,5*log₂0,5 + 0,5*log₂0,5) = 1.

Эта формула есть аналитическое определение бита по Шеннону: это среднее количество информации, которое содержится в двух равновероятных исходах некоторого опыта, составляющих полную группу событий.

Пример 5: Пусть, например, есть автомат, формирующий двузначные десятичные целые положительные числа (исходное множество информационных элементов {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}).

Автомат генерирует размещения:

Числа 34, 43 - из 10 элементов (используются 10 цифр) по 2

с повторениями - 33, 66 из одинаковых цифр.

Можно оценить, сколько различных сообщений (двузначных чисел) может сформировать автомат,

иначе говоря, можно оценить информационную емкость данного устройства: Рп(10²) = 10² = 100.

Дата добавления: 2014-01-06