
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Сводка теории. Общее представление об исчислении предикатов
Общее представление об исчислении предикатов
Задачи
3.1. Являются ли выводами в ИВ следующие последовательности формул:
а)  ;
;
б)  ,
, 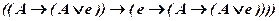 ,
, 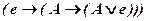 ;
;
в)  ,
,  , В?
, В?
3.2. Вывести в ИВ формулы:
а) 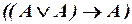 ;
;
б)  .
.
Аксиоматический метод, без которого можно было обойтись (ввиду наличия эффективного метода истинностных таблиц) при рассмотрении исчисления высказываний, становится необходимым для изучения формул, содержащих кванторы, поэтому обратимся к теориям первого порядка (или, иначе, элементарным теориям).
Слова «первого порядка» указывают на отличие рассматриваемых теорий от таких теорий, в которых либо допускаются предикаты, имеющие в качестве возможных значений своих аргументов другие предикаты и функции, либо допускаются кванторы по предикатам или кванторы по функциям. Теорий первого порядка хватает для выражения известных математических теорий и, во всяком случае, большинство теорий высших порядков может быть подходящим образом «переведено» на язык первого порядка.
Фиксируем логико-математический язык первого порядка L. Аксиомами исчисления предикатов (ИП) в языке L называются формулы этого языка, имеющие один из следующих видов:
 , (ип1)
, (ип1)
 , (ип2)
, (ип2)
 , (ип3)
, (ип3)
 , (ип4)
, (ип4)
 , ип5)
, ип5)
 , (ип6)
, (ип6)
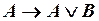 , (ип7)
, (ип7)
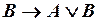 , (ип8)
, (ип8)
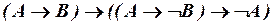 , (ип9)
, (ип9)
 , (ип10)
, (ип10)
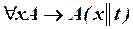 , (ип11)
, (ип11)
 , (ип12)
, (ип12)
 , (ип13)
, (ип13)
 . (ип14)
. (ип14)
Здесь A, B, C – произвольные формулы языка L, так что каждая строка приведенного списка задает схему аксиом ИП. Фиксируя A, B, C, из каждой из четырнадцати схем аксиом можно получить бесконечное семейство конкретных аксиом. Далее 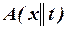 означает правильную подстановку терма вместо переменной с необходимыми переименованиями связанных переменных. Вместо
означает правильную подстановку терма вместо переменной с необходимыми переименованиями связанных переменных. Вместо 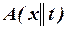 будем иногда несколько неточно писать A(t). В схемах (ип12) и (ип14) формула C не содержит свободной переменной x.
будем иногда несколько неточно писать A(t). В схемах (ип12) и (ип14) формула C не содержит свободной переменной x.
С помощью уже рассмотренных нами методов нетрудно убедиться, что все аксиомы ИП суть логические законы, общезначимые формулы (т.е. тавтологии).
Фигуры следующих двух видов называются правилами вывода ИП:
(MP)  , (Gen)
, (Gen) 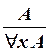 .
.
Первое правило вывода носит традиционное латинское название – модус поненс (modus ponens). Второе правило называется правилом обобщения (Gen – от английского слова «generalization»). Оба правила сохраняют логические законы: если выше черты стоят тавтологии, то формула ниже черты также тавтология).
Дерево формул (в ИП) есть по определению некоторая двумерная фигура, составленная из формул языка по следующим трем индуктивным правилам:
1) каждая формула A сама по себе является деревом формул, нижней формулой этого дерева формул считается по определению формула A;
2) если 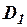 и
и  – деревья формул с нижними формулами вида A и
– деревья формул с нижними формулами вида A и  соответственно, то фигура
соответственно, то фигура 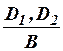 есть дерево формул. Говорят, что формула Bполучена в этом дереве из A и
есть дерево формул. Говорят, что формула Bполучена в этом дереве из A и  по правилу (MP); нижней формулой результирующего дерева является формула B;
по правилу (MP); нижней формулой результирующего дерева является формула B;
3) если 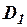 – дерево формул с нижней формулой A и x – переменная, то фигура
– дерево формул с нижней формулой A и x – переменная, то фигура 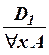 есть также дерево формул. Говорят, что нижняя формула
есть также дерево формул. Говорят, что нижняя формула  этого дерева получена из A по правилу (Gen).
этого дерева получена из A по правилу (Gen).
Последовательность вхождений формул в дерево формул, начинающаяся с нижней формулы дерева и продолжающаяся без пропусков до одной из самых верхних формул дерева, называется ветвью дерева формул. Количество формул в самой длинной ветви дерева называется высотой дерева формул. Верхние формулы дерева формул, не имеющие вида аксиом ИП, называются гипотезами, или открытыми посылками, дерева. Формула B, входящая в вывод, расположена выше формулы A, если существует ветвь вывода, содержащая A и B, причем B в этой ветви встречается позже, чем A.
Деревом вывода, или просто выводом, в ИП называется дерево формул, удовлетворяющее некоторому дополнительному структурному требованию. А именно, если формула  получена в выводе из формулы A по правилу (Gen), то переменная x не входит свободно в гипотезы, расположенные выше рассматриваемого вхождения формулы
получена в выводе из формулы A по правилу (Gen), то переменная x не входит свободно в гипотезы, расположенные выше рассматриваемого вхождения формулы  .
.
Если формула  получена в дереве формул из формулы A по правилу (Gen), а формула B расположена в дереве формул выше рассматриваемого вхождения
получена в дереве формул из формулы A по правилу (Gen), а формула B расположена в дереве формул выше рассматриваемого вхождения  и содержит свободно x, то говорят, что переменная xварьируется в формуле B. Тогда структурное требование можно выразить следующим образом: в выводе параметры гипотез не варьируются, остаются свободными.
и содержит свободно x, то говорят, что переменная xварьируется в формуле B. Тогда структурное требование можно выразить следующим образом: в выводе параметры гипотез не варьируются, остаются свободными.
Структурное требование выполняется тривиально, если дерево формул не содержит правил (Gen), или если все гипотезы дерева формул суть замкнутые формулы, или если дерево формул вовсе не содержит гипотез.
Пусть Г – конечный список формул и A – формула. Говорят, что формула Aвыводима в ИП из списка формул Г, и пишут Г  A, если существует вывод D с нижней формулой A такой, что всякая гипотеза D является членом списка Г. При этом, конечно, некоторые формулы из Г могут и не быть гипотезами D. Говорят, что вывод D формулы Aне зависит от таких членов Г.
A, если существует вывод D с нижней формулой A такой, что всякая гипотеза D является членом списка Г. При этом, конечно, некоторые формулы из Г могут и не быть гипотезами D. Говорят, что вывод D формулы Aне зависит от таких членов Г.
Список Г может быть пуст. Тогда Г  A означает, что имеется вывод Aбез гипотез; тогда пишут
A означает, что имеется вывод Aбез гипотез; тогда пишут  A и говорят: формула Aвыводима в ИП.
A и говорят: формула Aвыводима в ИП.
Саму фигуру Г  A называют иногда выводимостью (или, в другой терминологии, секвенцией). Таким образом, чтобы обосновать секвенцию Г
A называют иногда выводимостью (или, в другой терминологии, секвенцией). Таким образом, чтобы обосновать секвенцию Г  A, следует построить вывод в ИП с нижней формулой A, все гипотезы которого находятся среди членов списка Г.
A, следует построить вывод в ИП с нижней формулой A, все гипотезы которого находятся среди членов списка Г.
Непосредственно использовать выводы в ИП для установления логических законов на практике крайне неудобно. Выводы даже простых формул получаются очень громоздкими, а главное, весьма непохожими на обычные способы рассуждения, применяемые в математике. Поэтому понятие вывода в ИП используется, главным образом, в теоретических исследованиях, где существенно, чтобы выводы имели простую структуру.
Практически же выводимость формул и секвенций устанавливается с помощью серии специально подобранных допустимых вспомогательных правил вывода, относящихся непосредственно к секвенциям. С их помощью можно установить, что секвенция выводима, не строя для нее вывод в ИП. Указанные правила уже близко соответствуют обычной практике математического рассуждения, что сильно облегчает доказательство выводимости. Набор этих правил называется техникой естественного вывода.
Ключевым фактом здесь является следующая теорема.
Теорема 3.1 (о дедукции )
 |
Если Г, A
 B, то Г
B, то Г 
 . Этот факт записывается в виде вспомогательного правила вывода:
. Этот факт записывается в виде вспомогательного правила вывода:
Теорема о дедукции показывает, что для установления импликации
Г 
 достаточно показать Г, A
достаточно показать Г, A  B, что часто бывает гораздо проще. В математической практике этому соответствует следующий пример рассуждения. Если нужно в некоторой ситуации установить, что
B, что часто бывает гораздо проще. В математической практике этому соответствует следующий пример рассуждения. Если нужно в некоторой ситуации установить, что  , то допустим (введем гипотезу), что A верно, и докажем B, исходя из этой гипотезы.
, то допустим (введем гипотезу), что A верно, и докажем B, исходя из этой гипотезы.
Следующие правила называются структурными правилами техники естественного вывода:
| 1) закон тождества | A  A; A;
|
| 2) правило добавления |  Г Г  A
Г,B A
Г,B  A; A;
|
| 3) правило перестановки | Г, B, C, D  A A
 Г, C, B, D Г, C, B, D  A; A;
|
| 4) правило сокращения |  Г, B, B, C Г, B, B, C  A
Г, B, C A
Г, B, C  A; A;
|
| 5) правило сечения | Г  A; B, A A; B, A  C C
 Г, B Г, B  C. C.
|
Правила 2 – 5 следует понимать как допустимые правила вывода. Это означает, что если дан вывод для секвенций, расположенных выше черты, то можно построить вывод и для секвенций, расположенных ниже черты. В технике естественного вывода данные правила широко употребляются без явного упоминания.
Следующую группу образуют логические правила техники естественного вывода. Эти правила разбиваются на группы: для каждой логической связки и квантора – своя группа правил. Кроме того, внутри группы правила делятся на два вида: правила введения, указывающие, как доказывать формулу с данным логическим символом, и правила удаления, указывающие, как использовать формулу с данным логическим символом для доказательства других формул:
| Логические операции и кванторы | Правила | |
| Введение | Удаление | |
| 1) Импликация |  Г, А Г, А  В
Г В
Г  A A 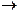 В В
| Г  A; Г A; Г  A A 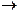 В В
 Г Г  В В
|
| 2) Конъюнкция | Г  A; Г A; Г  В В
 Г Г  A ^ B A ^ B
| Г, A, B  C C
 Г, A ^ B Г, A ^ B  C C
|
| 3) Дизъюнкция | Г  AГ AГ  B B
  Г Г  A Ú B Г A Ú B Г  A Ú B A Ú B
| Г, A  C; Г, B C; Г, B  C C
 Г, A Ú B Г, A Ú B  C C
|
| 4) Отрицание | Г, A  B; Г, A B; Г, A  Ø B Ø B
 Г Г  Ø A Ø A
|  Г Г  ØØ A
Г ØØ A
Г  A A
|
| Логические операции и кванторы | Правила | |
| Введение | Удаление | |
| 5) Общность |  Г Г  A (y)
Г A (y)
Г  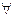 xA (x)
(здесь y не входит свободно в Г, и если x отлично от y, то x не входит свободно в A(y)); xA (x)
(здесь y не входит свободно в Г, и если x отлично от y, то x не входит свободно в A(y));
|  Г Г  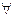 xA
Г xA
Г  A (x A (x 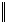 t) t)
|
| 6) Существование: |  Г Г  A (x A (x 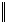 t)
Г t)
Г   x A x A
|  Г, A (y) Г, A (y) C
Г, C
Г,  x A(x) x A(x)  C
(здесь y не входит свободно в Г и C, и если x отлично от y, то x не входит свободно в A(y), A(x) есть A (y C
(здесь y не входит свободно в Г и C, и если x отлично от y, то x не входит свободно в A(y), A(x) есть A (y 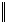 x)) x))
|
| 7) Эквивалентность |  Г, A Г, A  B; Г, B B; Г, B  A
Г A
Г  A A 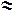 B B
|  Г Г  A; Г A; Г  A A 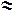 B
Г B
Г  B
Г B
Г  B; Г B; Г  A A 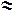 B B
 Г Г  A A
|
На практике логические правила применяются, так сказать, в обратном порядке: нужно установить секвенцию ниже черты, и мы замечаем, что для этого достаточно установить секвенцию выше черты. В этом свете можно заметить, что все правила соответствуют довольно обычным приемам математического рассуждения.
Например:
Ú-удаление соответствует разбору случаев. Если в некоторой ситуации из A Ú B нужно вывести C, то мы рассуждаем так: если верно A Ú B, то либо A, либо B, и поэтому достаточно разобрать случаи, вывести C из A и вывести C из B по отдельности;
 -удаление соответствует правилу единичного выбора (в другой терминологии, правилу С). Допустим, что
-удаление соответствует правилу единичного выбора (в другой терминологии, правилу С). Допустим, что  x A(x), и выведем C. Раз существует x, такое, что A(x), то можно рассмотреть (выбрать) одно из таких x. Обозначим его через y. Для этого y верно A(y). Таким образом, достаточно вывести формулу C из A(y).
x A(x), и выведем C. Раз существует x, такое, что A(x), то можно рассмотреть (выбрать) одно из таких x. Обозначим его через y. Для этого y верно A(y). Таким образом, достаточно вывести формулу C из A(y).
Правило Ø-введения соответствует рассуждению от противного, приведению к абсурду (традиционное латинское название – reductio ad absurdum): чтобы установить Ø A, достаточно, допустив A, получить противоречие, т.е. вывести B и Ø B одновременно для подходящего B.
Руководствуясь этими идеями, можно доказывать выводимость логических законов, исходя из их содержательного смысла. Разумеется, в технике естественного вывода можно использовать и другие секвенции, выводимости которых уже установлены, или иные допустимые правила.
Еще одно полезное правило – правило подстановки:
Г  A
A
 Г (
Г (
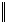
 )
) A (
A (
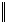
 ).
).
|
Дата добавления: 2014-01-06; Просмотров: 313; Нарушение авторских прав?; Мы поможем в написании вашей работы!