
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Интегральная теорема Лапласа
|
|
|
|
Вновь предположим, что производится n испытаний, в каждом из которых вероятность появления события А постоянна и равна р (0 < р < 1). Как вычислить вероятность 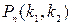 того, что событие А появится в n испытаниях не менее
того, что событие А появится в n испытаниях не менее 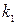 и не более
и не более 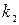 раз (для краткости будем говорить «от
раз (для краткости будем говорить «от 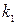 до
до 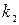 раз»)? На этот вопрос отвечает интегральная теорема Лапласа, которую мы приводим ниже.
раз»)? На этот вопрос отвечает интегральная теорема Лапласа, которую мы приводим ниже.
Теорема. Если вероятность р наступления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность 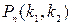 того, что событие А появится в n испытаниях от
того, что событие А появится в n испытаниях от 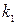 до
до 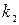 раз, приближенно равна определенному интегралу
раз, приближенно равна определенному интегралу  ,
,
где 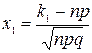 и
и  .
.
При решении задач, требующих применения интегральной теоремы Лапласа, пользуются специальными таблицами, так как неопределенный интеграл  не выражается через элементарные функции. Таблица для интеграла
не выражается через элементарные функции. Таблица для интеграла 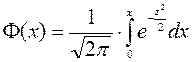 приведена в приложении (см. приложение 2). В таблице даны значения функции Ф(х) для положительных значений х и для х=0; для х<0 пользуются той же таблицей (функция Ф(х) нечетна, т. е. Ф(-х)=-Ф(х)). В таблице приведены значения интеграла лишь до х = 5, так как для х>5 можно принять Ф(х)=0,5. Функцию Ф(х) часто называют функцией Лапласа.
приведена в приложении (см. приложение 2). В таблице даны значения функции Ф(х) для положительных значений х и для х=0; для х<0 пользуются той же таблицей (функция Ф(х) нечетна, т. е. Ф(-х)=-Ф(х)). В таблице приведены значения интеграла лишь до х = 5, так как для х>5 можно принять Ф(х)=0,5. Функцию Ф(х) часто называют функцией Лапласа.
Итак, вероятность того, что событие А появится в n независимых испытаниях от 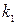 до
до 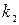 раз,
раз,  ,
,
где 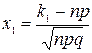 и
и  .
.
Пример. Вероятность того, что деталь не прошла проверку ОТК, равна р=0,2. Найти вероятность того, что среди 400 случайно отобранных деталей окажется непроверенных от 70 до 100 деталей.
Решение: По условию, р=0,2; q=0,8; n=400; 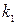 =70;
=70; 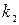 =100. Воспользуемся интегральной теоремой Лапласа:
=100. Воспользуемся интегральной теоремой Лапласа:  .
.
Вычислим нижний и верхний пределы интегрирования.
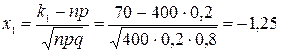 ;
; 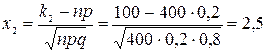 .
.
Таким образом, имеем
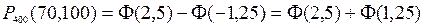 .
.
По таблице приложения 2 находим: Ф(2,5)=0,4938; Ф(1,25)=0,3944.
Искомая вероятность  .
.
|
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 514; Нарушение авторских прав?; Мы поможем в написании вашей работы!