Общие методы определения перемещений в упругих системах

Лекция 11

ОБОБЩЁННЫЕ СИЛЫ И ОБОБЩЕННЫЕ ПЕРЕМЕЩЕНИЯ

Во многих случаях не требуется находить перемещения как функции координат, достаточно уметь вычислять перемещения в конкретных точках конструкции по заданным направлениям.

Эту задачу можно решить, основываясь на фундаментальных принципах механики - начале возможных перемещений и законе сохранения энергии.

Работа постоянной силы F на перемещении в направлении силы Δ _F равна произведению

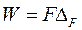. (11.1)

Поскольку нагрузки в задачах сопротивления материалов довольно разнообразны и, как правило, представляют собой группы воздействий сосредоточенных сил и моментов, погонных нагрузок и т.д., введём понятие обобщённой силы, под которой будем понимать любую внешнюю нагрузку.

Обобщённым перемещением будем называть тот вид перемещения точек конструкции, на котором обобщённая сила совершает работу.

Так, например, если обобщённая сила представляет собой действующую на балку сосредоточенную силу, обобщённым перемещением будет прогиб балки в месте приложения силы. Обобщённой силе в виде сосредоточенного момента будет соответствовать обобщённое перемещение в виде угла поворота сечения. Для стержня, растянутого приложенными на концах силами F, за обобщенную силу можно принять величину F, а за обобщённое перемещение – изменение расстояния между точками приложения силы, т.е. удлинение стержня.

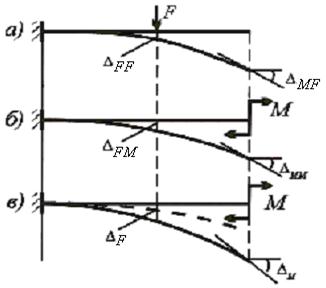В дальнейшем обобщённые перемещения будем обозначать греческой буквой Δ с двумя индексами. Первый индекс указывает точку и направление перемещения, второй – его причину, т.е. вызвавшую данное перемещение нагрузку. При обозначенииполного перемещения от нескольких воздействий второй индекс опускается. На рис. 11.1 показаны обобщённые перемещения в консольной балке, нагруженной сосредоточенными силой и моментом.

Рис. 11.1

Прогиб балки в месте приложения силы F от воздействия самой силы обозначен Δ _FF (см. рис.11.1, а), прогиб от действия момента М обозначен Δ _FМ (см. рис.11.1, б). Угловое перемещение в месте приложения момента от силы F обозначено как Δ _MF, а от действия момента M - Δ _МM. Полное перемещение от совместного действия нагрузок обозначено Δ _F и Δ _М соответственно (см. рис. 11.1, в).

Перемещения, вызванные обобщённой единичной безразмерной силой 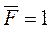, будем обозначать буквой δ с соответствующими индексами и называть удельными перемещениями. Так, d _ij – перемещение точки приложения i-ой единичной силы (в направлении этой силы) от действия j-ой обобщённой единичной силы. Под обобщёнными единичными силами могут выступать как сосредоточенные силы и моменты, так и группы этих воздействий.

ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ СТЕРЖНЕВОЙ СИСТЕМЫ

Для нахождения потенциальной энергии деформации выделим из стержня бесконечно малый элемент длиной dz. В общем случае нагружения в каждом из выделенных сечений возникает шесть внутренних силовых факторов – изгибающие и крутящий моменты, нормальная и поперечные силы. Работа, совершаемая этими внутренними усилиями при деформировании элемента, численно равна потенциальной энергии, накопленной в элементарном участке стержневой системы. При этом каждый из силовых факторов вызывает такую деформацию элемента, на которой остальные внутренние усилия не совершают работы. Так, если в качестве обобщённой силы взять нормальную силу N, то в качестве обобщённого перемещения будет выступать изменение длины элемента Δ dz. При этом потенциальная энергия деформации элемента определится через работу силы N по теореме Клапейрона:

С учётом закона Гука ,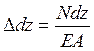

получим

.

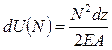Здесь принято, что сила в процессе деформации элемента не остаётся постоянной, а медленно возрастает от нуля до своего окончательного значения.

Потенциальная энергия деформации всей системы найдётся интегрированием по длине составляющих систему стержней

(11.2)

Если стержни работают только на растяжение и сжатие, то ,

в общем случае необходимо учесть вклад каждого из внутренних силовых факторов:

(11.3)

Для крутящего момента М _к обобщённым перемещением будет взаимный угол закручивания сечений элемента dφ. При этом

,

или, с учётом того, что 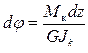,потенциальная энергия элемента

.

Интегрируя по длине всех элементов системы, получим

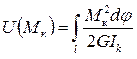. (11.4)

Аналогично находится вклад изгибающих моментов в потенциальную энергию системы:

(11.5)

Здесь учтено, что изгибающие моменты совершают работу на обобщённом перемещении, в качестве которого выступает взаимный угол поворота сечений

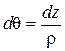, где кривизна оси элемента в каждой из двух плоскостей нагружения будет своей.

Наконец, получим выражение потенциальной энергии от действия поперечных сил. Для этого рассмотрим элемент балки, находящийся в состоянии плоского поперечного изгиба

Рис. 11.2

На рис. 11.2 заштрихована часть элемента, полученная двумя бесконечно близкими продольными сечениями, проведёнными на расстоянии у от нейтральной оси. На гранях этого элемента действуют нормальные и касательные напряжения (рис. 11.3).

Нормальные напряжения связаны с изгибающими моментами, вклад которых в потенциальную энергию системы мы уже рассмотрели.

Касательные напряжения вызывают параллельный сдвиг граней элемента на величину 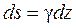, или с учётом закона Гука при сдвиге

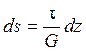, где G – модуль сдвига.

Рис. 11.3

Работа внутренних элементарных сил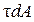на перемещении ds

.

После интегрирования по площади поперечного сечения A

.

Учитывая, что по формуле Журавского

,

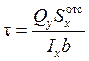получим

Здесь 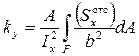- безразмерный коэффициент, зависящий от формы сечения. Для сечений простой формы его несложно вывести. Так для прямоугольника он равен 6/5; для круга – 10/9; для стандартных тонкостенных профилей k_y = 2…2,4.

Интегрируя по длине всех элементов системы, находим

.

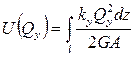Аналогично

.

Итак, в общем случае нагружения потенциальная энергия стержневой системы в соответствии с (11.3) находится следующим образом

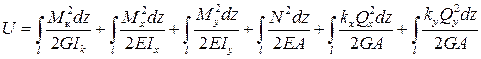(11.6)

Интегрирование в (11.6) ведётся по длине всех входящих в систему стержней.

Следует отметить, что не все слагаемые в этом выражении равнозначны по величине. Как правило, потенциальная энергия нормальных и поперечных сил значительно меньше энергии крутящих и изгибающих моментов и в практических расчётах ею можно пренебречь. Например, при плоском изгибе балок и рам потенциальную энергию деформации с достаточной для инженерных расчётов точностью можно вычислять с учётом только изгибающего момента:

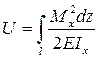(11.7)

ОПРЕДЕЛЕНИЕ ПРЕМЕЩЕНИЙ С ПОМОЩЬЮ ТЕОРЕМЫ КАСТИЛИАНО

Для упругих систем, подчиняющихся закону Гука, теорему Кастилиано можно сформулировать следующим образом:

. (11.8)

Здесь U – потенциальная энергия системы; F_i – некоторая обобщённая сила;

Δ _i – перемещение точки приложения силы по её направлению, т.е. соответствующее обобщённое перемещение.

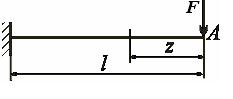Формула (11.8) позволяет найти обобщённое перемещение, соответствующее любой из приложенных к системе сосредоточенных обобщённых сил. Например, для показанной на рис. 11.4 балки, прогиб в точке А

Рис 11.4 определяется следующим образом.

Запишем выражение потенциальной энергии

.

Здесь учтено, что изгибающий момент в произвольном сечении z .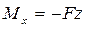

После интегрирования получаем

Дата добавления: 2014-01-06