
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Точные методы решения
|
|
|
|
К числу распространённых относятся метод Гаусса и его модификация, называемая методом Жордана – Гаусса.
Метод Гаусса. Центральной частью данного метода является процедура приведения исходной системы уравнения к треугольному, в общем случае, трапецеидальному, виду. Это осуществляется путём эквивалентных преобразований системы в следующей последовательности.
Шаг 1. В левой части первого уравнения выбирается отличный от нуля коэффициент, который называется ведущим или определяющим. Пусть это 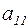 , в противном случае добьемся этого, переставив столбцы и перенумеровав неизвестные. После этого разделим первое уравнение на ведущий элемент
, в противном случае добьемся этого, переставив столбцы и перенумеровав неизвестные. После этого разделим первое уравнение на ведущий элемент
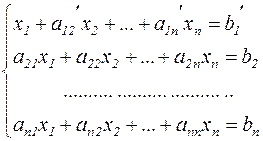 .
.
Шаг 2. Вычтем почленно из второго уравнения первое, умноженное на 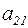 , далее, из третьего первое, умноженное на
, далее, из третьего первое, умноженное на  и т.д., наконец из n-го,- первое, умноженное на
и т.д., наконец из n-го,- первое, умноженное на 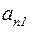 . В результате этого получим
. В результате этого получим
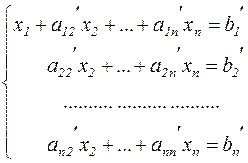 .
.
Шаг 3. Первое уравнение оставим неизменным, а во втором,- выберем ведущий элемент, пусть это  и разделим на него второе уравнение.
и разделим на него второе уравнение.
Шаг 4. Из третьего и всех последующих уравнений, описанным выше способом, исключим переменную х2.
Далее, поступая таким же образом с третьим и остальными уравнениями за конечное число шагов приведём систему к треугольному виду
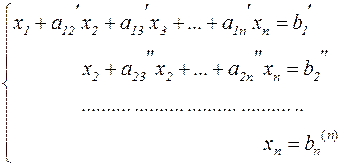 (3.2)
(3.2)
если решение единственно, или к трапецеидальному, если решений бесконечно много. Если же на каком-то шаге одно из уравнений примет вид 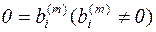 , то это означает несовместимость исходной системы уравнений.
, то это означает несовместимость исходной системы уравнений.
Описанный процесс преобразования системы называется прямым ходом. Предположим, что в результате выполнения прямого хода система приведена к виду (3.2). В этом случае из последнего уравнения определяется значение  . Оно подставляется в предыдущее, из которого находится
. Оно подставляется в предыдущее, из которого находится 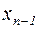 . Найденные значения
. Найденные значения  ,
, 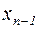 подставляются в (n -2)-е уравнение, из которого находится
подставляются в (n -2)-е уравнение, из которого находится 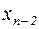 . Далее, действуя аналогичным образом, из (n -3)-го уравнения определяется значение
. Далее, действуя аналогичным образом, из (n -3)-го уравнения определяется значение 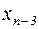 , из (n -4)-го, -
, из (n -4)-го, -  и, наконец, из первого – значение
и, наконец, из первого – значение 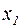 . Процесс последовательного нахождения
. Процесс последовательного нахождения  из системы (3.2) называется обратным ходом.
из системы (3.2) называется обратным ходом.
|
|
|
С целью снижения влияния погрешностей округления, возникающих при выполнении вычислений, в качестве ведущего рекомендуется выбирать наибольший по модулю элементы левой части уравнения. Действительно, в этом случае коэффициенты 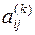 системы (3.2) по модулю не превышают единицу и частичные погрешности значения xi, обусловленные ошибками
системы (3.2) по модулю не превышают единицу и частичные погрешности значения xi, обусловленные ошибками  значений xm
значений xm
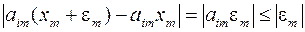
не превышает величины  , т.е. не возрастают.
, т.е. не возрастают.
Метод Жордана -Гаусса. Совмещает выполнение прямого и обратного ходов метода Гаусса. Реализуется следующим образом.
Шаг 1, 2, 3. Совпадают с первыми шагами метода Гаусса.
Шаг 4. С помощью второго уравнения переменная 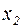 удаляется не только из последующих, но и из предыдущего, т.е. первого уравнения. В результате этого система принимает вид
удаляется не только из последующих, но и из предыдущего, т.е. первого уравнения. В результате этого система принимает вид
 .
.
Далее, рассматривается третье уравнение и с его помощью описанным образом исключается переменная 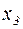 из всех остальных уравнений. Поступая также с каждым следующим уравнением, и проводя, быть может, переобозначение неизвестных, за конечное число шагов система приводится к виду
из всех остальных уравнений. Поступая также с каждым следующим уравнением, и проводя, быть может, переобозначение неизвестных, за конечное число шагов система приводится к виду
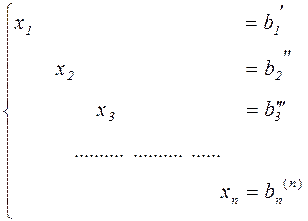 .
.
Столбец правых частей и представляет собой решение системы уравнений.
Сравнительный анализ. С точки зрения трудоёмкости вычислений оба метода практически эквивалентны. Так, для реализации метода Гаусса необходимо 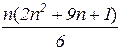 арифметических операций, для выполнения метода Жордана-Гаусса,-
арифметических операций, для выполнения метода Жордана-Гаусса,- 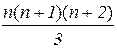 .
.
Вместе с тем, в литературе отмечается интересная особенность метода Жордана-Гаусса. А именно, если внести некоторые изменения в порядок его выполнения, то можно достичь существенного снижения необходимого объёма оперативной памяти. Так, рассматривая второе уравнение, использовать первое для исключения в нем переменной х1, после чего использовать модифицированное второе для исключения переменной х2 из первого уравнения. Далее, при рассмотрении третьего уравнения использовать первые два для исключения в них переменных х1, х2, после чего использовать третье для исключения из первых двух переменных х3. И так далее. При такой организации вычислений на каждом шаге в работе участвует не вся система, а только её часть. Показано, что при равных объёмах используемой оперативной памяти это позволяет примерно в два раза, по сравнению с методом Гаусса, повысить порядок решаемой системы.
|
|
|
Замечание. К числу точных относятся и методы, основанные на разложении матрицы А левой части системы (3.11) в виде произведения двух треугольных матриц В и С, т.е. А=ВС, где
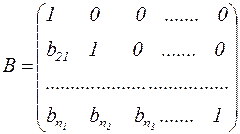 ,
, 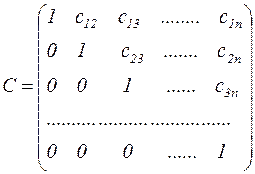 .
.
В этом случае система принимает вид
BСХ=b,
и, обозначив Y=CX, вместо системы (3.11), имеем две системы уравнений с треугольными матрицами
BY=b
CX=Y.
Центральным моментом таких методов является реализация указанного разложения матрицы А. Показано, что для симметрических и невырожденных матриц такие процедуры существуют.
3.3. Приближённые методы решения
При использовании приближённых методов предполагается, что система (3.11) представлена в виде
x=Bx+d, (3.3)
который называется нормальной формой системы уравнений.
Процесс вычислений в этом случае организуют следующим образом. По тем или иным соображениям выбирается начальное приближение  к решению системы. Оно подставляется в правую часть (3.3), полученное значение обозначается через
к решению системы. Оно подставляется в правую часть (3.3), полученное значение обозначается через 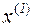 , принимается в качестве следующего приближения и подставляется в правую часть для получения
, принимается в качестве следующего приближения и подставляется в правую часть для получения  и т.д. Таким образом, вычислительный процесс описывается формулой
и т.д. Таким образом, вычислительный процесс описывается формулой
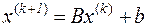 (3.4)
(3.4)
и называется итерационным. Процедура получения очередного приближения называется итерацией. После выполнения ряда таких итераций одно из приближений и принимается в качестве приближённого решения. Оценка полученной при этом погрешности и вопросы сходимости последовательности 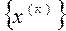 рассмотрим ниже. Описанная процедура приближённого решения системы уравнений называется методом простой итерации.
рассмотрим ниже. Описанная процедура приближённого решения системы уравнений называется методом простой итерации.
|
|
|
Модификацией этого метода является метод Зейделя. Его отличие состоит в том, что при получении компонент (к+ 1) - го приближения используются полученные на этой же итерации «улучшенные» значения предыдущих компонент. Математически этот процесс описывается следующим способом
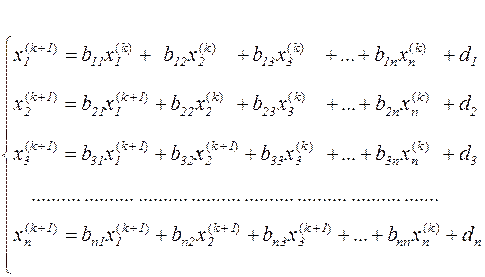 . (3.5)
. (3.5)
С целью ускорения сходимости в качестве очередной улучшаемой компоненты рекомендуется выбирать ту, которой соответствует наибольшее значение модуля невязки, т.е. значения 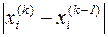 . Это реализуется так. После получения к -го приближения формируется вектор
. Это реализуется так. После получения к -го приближения формируется вектор
 ,
,
компоненты которого упорядочиваются по убыванию их модулей. Установленный в результате этого порядок переносится и на последовательность вычисления компонент (к+ 1) - го приближения по правилам (3.5).
Можно показать, что стационарный метод Зейделя (3.5), т.е. когда порядок вычисления компонент неизменен, сводится к методу простой итерации. Действительно, обозначим через B1, B2 следующие матрицы
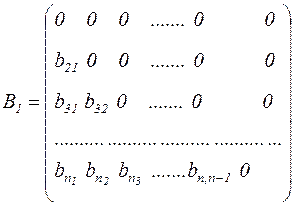 ,
, 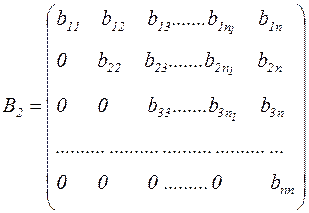
Тогда в матричном виде процесс (3.5) выглядит так
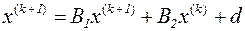 .
.
Отсюда
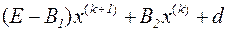
и
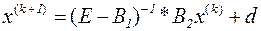 .
.
Таким образом, стационарный метод Зейделя с матрицей В эквивалентен методу простой операции с матрицей 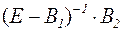 .
.
3.4. Сходимость и погрешность приближённых методов
Для описания сходимости вычислительного процесса и оценки погрешности приближённого решения необходимы дополнительные понятия.
погрешности приближённого решения необходимы дополнительные понятия.
Понятие нормы. Нормой вектора х, обозначается  , называется величина удовлетворяющая условиям:
, называется величина удовлетворяющая условиям:
1.  ;
;
2. 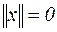

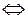 х=0; (3.6)
х=0; (3.6)
3. 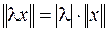 ;
;
4. 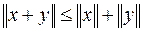 .
.
В теории метрических пространств получили распространение следующие типы норм:
1. 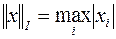 ;
;
2.  ;
;
3.  .
.
В зависимости от типа геометрической фигуры, получаемой в трёхмерном пространстве, описываемой условием 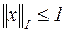 , первая из них называется кубической, вторая,- октаэдрической и третья,- сферической.
, первая из них называется кубической, вторая,- октаэдрической и третья,- сферической.
Нормой матрицы А, обозначается 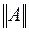 , называется величина, удовлетворяющая помимо требований (3.6) дополнительному условию
, называется величина, удовлетворяющая помимо требований (3.6) дополнительному условию
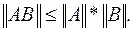
Обычно, используются одна из следующих норм:
1. 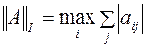 ;
;
2. 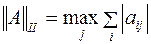 ;
;
3.  .
.
При одновременном использовании норм необходимо их согласование. А именно, норма вектора первого типа используется с нормой матрицы первого типа и т.д.
|
|
|
Понятие расстояния. Расстоянием между векторами x, y, обозначается символом 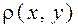 , называется величина
, называется величина
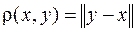 .
.
Из свойства 4 (3.6) следует важное для дальнейшего, так называемое, неравенство треугольника
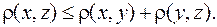
Действительно,

Сжимающие отображения. Пусть F,- некоторое отображение в линейном пространстве векторов. Оно называется сжимающим,- если существует такое число 
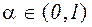 , что для любых векторов x, y выполняется соотношение
, что для любых векторов x, y выполняется соотношение
 .
.
Применительно к нормальной форме системы уравнений (3.3) в качестве F рассмотрим правую часть системы уравнений. А именно,
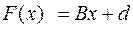 .
.
Тогда
 .
.
Таким образом, для того, чтобы отображение, определяемое системой (3.3) было сжимающим достаточно, чтобы одна из норм матрицы В была меньше 1.
Понятие сходимости. Пусть 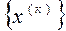 , где к = 1, 2, …,- некоторая бесконечная последовательность векторов. Говорят, что она сходится к вектору х по норме, если
, где к = 1, 2, …,- некоторая бесконечная последовательность векторов. Говорят, что она сходится к вектору х по норме, если

Последовательность 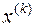 сходится к вектору
сходится к вектору 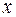 покомпонентно, если
покомпонентно, если
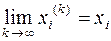 для
для  .
.
Нетрудно показать, что два эти понятия в некотором роде эквивалентны. А именно, если последовательность  сходится по норме, то она сходится покомпонентно и наоборот.
сходится по норме, то она сходится покомпонентно и наоборот.
При анализе сходимости последовательностей центральное место принадлежит признаку Коши:
Последовательность 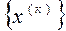 сходится тогда и только тогда, когда для сходится тогда и только тогда, когда для 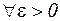  такой номер такой номер  , что для , что для  и и 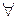 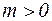 выполняется выполняется
 (или
(или  для для  ). ).
|
Сходимость итерационного процесса. Оценка погрешности. Пусть 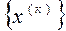 ,- итерационная последовательность, т.е.
,- итерационная последовательность, т.е.
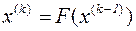 , (3.7)
, (3.7)
где 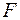 ,- сжимающее отображение с коэффициентом сжатия
,- сжимающее отображение с коэффициентом сжатия 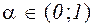 .
.
Рассмотрим 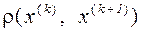 . По индукции имеем
. По индукции имеем
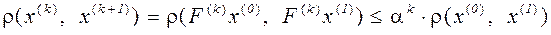 . (3.8)
. (3.8)
Далее, по свойству треугольников и с учетом (3.8), справедливым оказывается соотношение
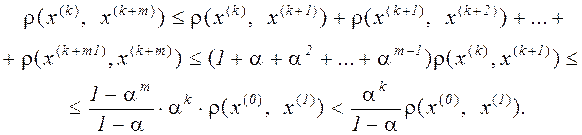 (3.9)
(3.9)
Потребовав теперь, чтобы
 ,
,
очевидно, можно найти номер  , начиная с которого
, начиная с которого  для
для  , m > 0.
, m > 0.
Таким образом, для сжимающего отображения признак Коши выполнен и, следовательно, итерационный процесс (3.7) сходится.
Оценим теперь погрешность к -го приближения, а именно, величину 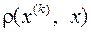 , где х - точное решение. С этой целью рассмотрим соотношение (см. (3.9))
, где х - точное решение. С этой целью рассмотрим соотношение (см. (3.9))
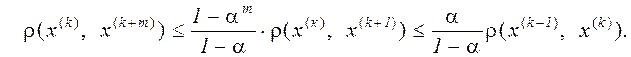
Переходя в нём к пределу при 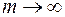 , получим, таким образом,
, получим, таким образом,
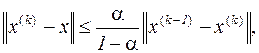 (3.10)
(3.10)
и доказанным становится утверждение:
| Если одна из норм матрицы B системы уравнений (3.3) меньше единицы, то итерационный процесс (3.4) является сходящимся при любом начальном приближении. Погрешность к -го приближения описывается соотношением (3.10). |
3.5 Приведение системы Ax=b к нормальному виду
Из предыдущего следует, что успех приближённого решения системы линейных алгебраических уравнений (3.1) во многом определяется возможностью её приведения к нормальному виду (3.3), для которого выполняется достаточные условия сходимости. Приведём некоторые соображения и рекомендации на этот счёт.
Первый вариант. Рассмотрим систему
Ах=b.
Представим матрицу А в виде суммы А=А1+А2, где det А1 ≠ 0. Тогда
(А1+А2) x=b,
отсюда
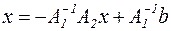 .
.
Обозначив через 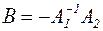 ,
, 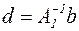 , получим
, получим
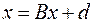 ,
,
что и требовалось. Тогда для того, чтобы обеспечить выполнение достаточного условия сходимости  , в качестве А1 достаточно взять матрицу близкую к А, т.е. А1≈А, в качестве А2, - «малую» матрицу
, в качестве А1 достаточно взять матрицу близкую к А, т.е. А1≈А, в качестве А2, - «малую» матрицу 
 .
.
Поясним это предложение на примере. Рассмотрим
 ,
,
Здесь 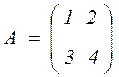 . Пусть
. Пусть
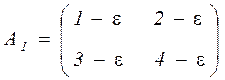 ,
,
Тогда  . Найдём
. Найдём 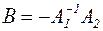 .
.
Имеем det А1 = -2 ≠ 0 и
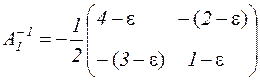 .
.
Тогда
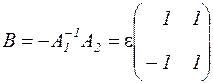
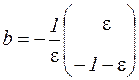
и система принимает вид
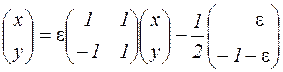 .
.
Очевидно, для сходимости метода итераций достаточно взять  .
.
Второй вариант. Состоит в следующем. Путём эквивалентных преобразований стараются добиться того, чтобы диагональные элементы в матрице А доминировали в левой части соответствующих уравнений, т.е. были по модулю существенно больше остальных. После этого каждое из уравнений делят на 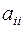 и, первое уравнение разрешают относительно
и, первое уравнение разрешают относительно 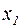 второе,- относительно
второе,- относительно 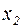 и т.д.
и т.д.
В качестве примера рассмотрим следующую систему
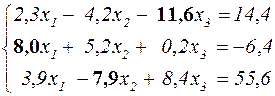
В результате анализа коэффициентов левой части уравнений производится их перестановка
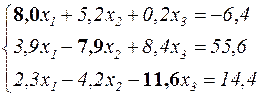
и для обеспечения доминирования во втором уравнении коэффициента  , который пока равен -7,9, ко второму уравнению прибавляется третье. В результате этого имеем
, который пока равен -7,9, ко второму уравнению прибавляется третье. В результате этого имеем

или, в нормальной форме,
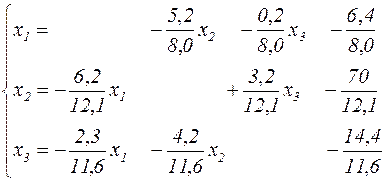 .
.
Здесь матрица
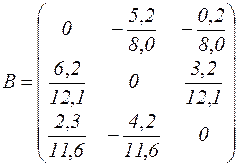 ,
,
очевидно, её норма 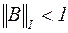 , и, следовательно, формируемый ею итерационный процесс сходится.
, и, следовательно, формируемый ею итерационный процесс сходится.
Третий вариант. Является обоснованным теоретически, формализуемым и, по этой причине, пожалуй, наиболее удобным. Он заключается в следующем.
Рассмотрим систему (3.11)
Ax=b
и предположим, что det А1 ≠ 0. Умножим обе части на 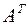 , получим
, получим
A1 x=b1,
где A1=АТА, b1= AT b. Здесь матрица A1 является симметрической, т.е. 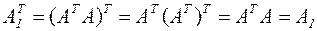 , причём её диагональные элементы
, причём её диагональные элементы  , в противном случае, по крайней мере, один из столбцов матрицы А равен нулю и, следовательно, det А = 0. Далее деля уравнение на диагональные элементы
, в противном случае, по крайней мере, один из столбцов матрицы А равен нулю и, следовательно, det А = 0. Далее деля уравнение на диагональные элементы 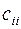 и, разрешая их относительно
и, разрешая их относительно 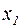 ,
, 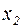 и т.д. получим нормальную систему
и т.д. получим нормальную систему
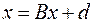 ,
,
где 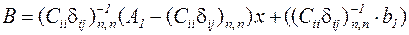 .
.
Показано, что для нормальной системы, полученной таким образом, метод Зейделя сходится.
|
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 344; Нарушение авторских прав?; Мы поможем в написании вашей работы!