Свойства сходящихся рядов

1) Если ряд сходится и имеет сумму 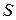, то и ряд также сходится и имеет сумму .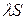

2) Если ряды и 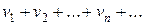сходятся и их суммы соответственно равны 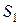и 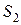, то и ряд 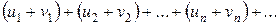также сходится и его сумма равна .

3) Если ряд сходится, то сходится и ряд, полученный из данного путем отбрасывания (или приписывания) конечного числа членов.

Если сумму 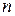-ого остатка ряда обозначить через , т.е.

,

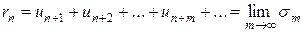то сумму ряда можно представить в виде:

4) Для того чтобы ряд сходился, необходимо и достаточно, чтобы при остаток ряда стремился к нулю, т.е. .

Установить сходимость (расходимость) ряда путем определения 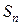и вычисления 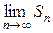можно сделать далеко не всегда из-за принципиальных трудностей при нахождении 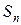. Проще это можно сделать на основании признаков сходимости.

2. НЕОБХОДИМЫЙ ПРИЗНАК СХОДИМОСТИ.

Теорема (необходимый признак сходимости). Если ряд сходится, то предел его общего члена 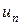при равен нулю, т.е.

.

Следствие. Если предел общего члена ряда 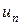при при не равен нулю, т.е. , то ряд расходится.

Пример 13.2. Исследовать сходимость ряда

Решение: Найдем 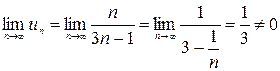- необходимый признак сходимости не выполняется. Значит ряд расходится.

Замечание. Рассмотренная теорема выражает лишь необходимый, но недостаточный признак сходимости ряда. Если , то из этого еще не следует, что ряд сходится.

3. РЯДЫ С ПОЛОЖИТЕЛЬНЫМИ ЧЛЕНАМИ (ДОСТАТОЧНЫЕ ПРИЗНАКИ СХОДИМОСТИ).

Теорема (признак сравнения). Пусть даны два ряда с положительными членам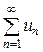и: (1) и (2), причем члены первого ряда не превосходят членов второго, т.е. при любом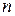

.

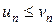Тогда: а) если сходится ряд 2, то сходится и ряд 1;

б) если расходится ряд 1, то сходится и ряд 2.

Замечание. Так как сходимость ряда не изменяется при отбрасывании конечного числа членов ряда, то условие 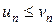не обязательно должно выполнятся с первых членов рядов и только для членов с одинаковыми номерами 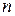. Достаточно, чтобы оно выполнялось, начиная с некоторого номера , или чтобы имело место неравенство 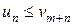, где - некоторое целое число.

«Эталонные ряды» (часто используемые для сравнения):

1) геометрический ряд 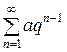- сходится при 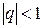, расходится при ;

2) гармонический ряд - расходится;

3) обобщенный гармонический ряд

сходится при , расходится при .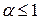

Нестандартность применения признака сравнения заключается в том, что надо не только подобрать соответствующий «эталонный» ряд, но и доказать неравенство 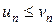, для чего часто требуется преобразование рядов (например, отбрасывание или приписывание конечного числа членов, умножение на определенные числа и т.п. В ряде случаев более простым оказывается предельный признак сравнения.

Пример 13.3. Исследовать на сходимость ряд

Решение. Т.к. 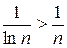, а гармонический ряд 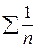расходится, то расходится и ряд .

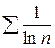Пример.13.4 Исследовать на сходимость ряд .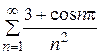

Решение. Ряд дан знакоположительный. Т.к. 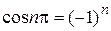, т.е. он может быть равен 1 или–1, то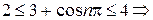 . Из последнего неравенства видно, что исходный ряд можно сравнить с рядом , а этот ряд сходится (обобщенный гармонический с p =2>1, все члены которого умножены на 4). Но т.к. ряд с большими членами сходится, то на основании признака сравнения в непредельной форме будет сходиться и исходный ряд.

Теорема (предельный признак сравнения). Есл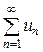и и - ряды с положительными членами и существует конечный предел отношения их общих членов 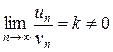, то ряды одновременно сходятся либо расходятся.

Пример 13.5. Исследовать сходимость ряда

.

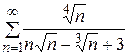Решение. Ряд знакоположительный, применим к нему признак сравнения в предельной форме, сравнив его с рядом 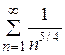, который сходится как обобщенный гармонический ряд с . .

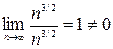Предел отношения общих членов этих рядов при конечный, не равный нулю, следовательно, ряды ведут себя одинаково; данный ряд сходится. Ряд для сравнения подбираем следующим образом: при ;

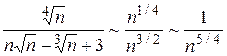
Теорема (признак Даламбера). Пусть для ряда 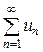с положительными членами существует предел отношения 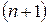-го члена к 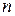-му члену 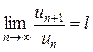. Тогда, если 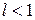, то ряд сходится; если 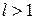, то ряд расходится; если 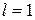, то вопрос о сходимости остается нерешенным.

Замечание. Если 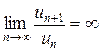, то ряд расходится.

Признак эффективен в случае наличия в общем члене ряда показательной функции или факториалов.

Пример 13.6. Определить сходимость ряда .

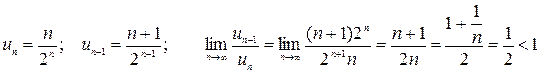
Вывод: ряд сходится.

Пример 13.7. Определить сходимость ряда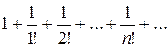

Вывод: ряд сходится.

Пример 13.8. Применим признак Даламбера к исследованию сходимости ряда .

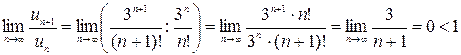, следовательно, ряд сходится (учитываем, что (п + 1)! = п!(п + 1)).

Пример 13.9. Исследовать сходимость ряда c помощью признака Даламбера.

Решение:

Здесь .

Тогда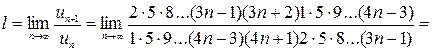

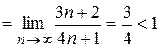. Ряд сходится, т.к. 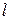<1.

Пример 13.10. Исследовать сходимость ряда .

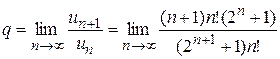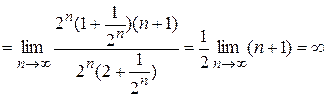, = . Т.к. q >1, ряд расходится.

Теорема (интегральный признак сходимости). Пусть дан ряд 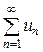, члены которого положительны и не возрастают, т.е. 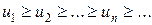, а функция 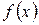, определенная при , непрерывная и невозрастающая и

.

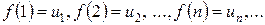Тогда для сходимости ряда 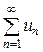необходимо и достаточно, чтобы сходился несобственный интеграл .

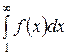4. РЯДЫ С ЧЛЕНАМИ ПРОИЗВОЛЬНОГО ЗНАКА

Знакочередующиеся ряды. Под знакочередующимся рядом понимается ряд, в котором члены попеременно то положительны, то отрицательны: , где .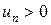

Теорема (признак Лейбница). Если члены знакочередующегося ряда убывают по абсолютной величине 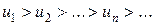и предел его общего члена при равен нулю, т.е. , то ряд сходится, а его сумма не превосходит первого члена: .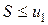

Пример 13.11. Исследовать сходимость ряда .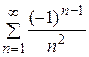

Ñ Ряд знакочередующийся. Применим признак Лейбница (теорема 7). ,

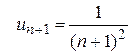. Очевидно, что 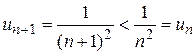. Кроме того, 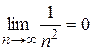. Выполнены оба условия признака Лейбница, следовательно, ряд сходится. #

Пример 13.12. Исследовать сходимость ряда .

Ñ Дан знакочередующийся ряд. Члены этого ряда по абсолютной величине монотонно убывают. В самом деле, 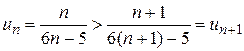, т.к. 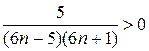. Однако, 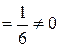. Значит, ряд расходится по необходимому признаку (теорема 1, следствие), по признаку Лейбница расходимость не установить. #

Знакопеременные ряды. Пусть знакопеременный ряд, в котором любой его член 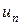может быть как положительным, так и отрицательным.

Теорема (достаточный признак сходимости знакопеременного ряда). Если ряд, составленный из абсолютных величин членов данного знакопеременного ряда сходится, то сходится и данный ряд.

Определение 1. Ряд называется абсолютно сходящимся, если сходится как сам ряд, так и ряд, составленный из абсолютных величин его членов.

Определение 2. Ряд называется условно сходящимся, если сам ряд сходится, а ряд, составленный из абсолютных величин его членов, расходится.

Пример 13.13. Исследовать сходимость ряда .

ÑДан знакопеременный ряд. Применим к нему признак абсолютной сходимости. Составим ряд из абсолютных величин членов исходного ряда: . Этот знакоположительный ряд сравним в непредельной форме с рядом , который представляет собой геометрическую прогрессию с , следовательно, сходится. Имеем очевидное неравенство: 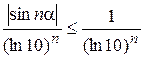, тогда ряд также сходится, а значит по признаку абсолютной сходимости исходный ряд сходится абсолютно.#

Пример 13.14. Исследовать на абсолютную или условную сходимость так называемый ряд Лейбница

Ñ По признаку Лейбница (теорема 7) этот ряд сходится, т.к. для него выполняются оба условия этого признака: a) и б) 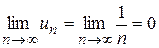. Но ряд, составленный из абсолютных величин данного ряда, является гармоническим, который расходится. Следовательно, ряд Лейбница сходится условно. #

СТЕПЕННЫЕ РЯДЫ. СВОЙСТВА СТЕПЕННЫХ РЯДОВ

Степенным рядом называется ряд вида

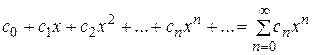(4.1)

т.е. ряд, членами которого являются степенные функции. Всякий степенной ряд (4.1) сходится в интервале 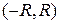. R называется радиусом сходимости ряда (4.1).

Если R = 0, то ряд (4.1) сходится только в точке x = 0. Если , то ряд (4.1) сходится на всей числовой оси. Если 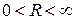, то интервалом сходимости является конечный интервал с центром в точке x = 0.

Более общий вид степенного ряда:

. (4.2)

Интервал сходимости этого ряда симметричен относительно точки : .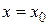

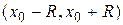Дата добавления: 2014-01-06