Вынужденные колебания систем с конечным числом степ. свободы при силовом гармоническом возмущении

Лекция №9

Сдельный автопоезд

О – момент инерции во вращательном движении относительно седла

Предположим только одну возможную силу, заданную по 3-му.

Для расчёта динамической системы на движение нескольких сил достаточно получить решение для одной из действующих сил. Последние примеры независимости действия сил позволяет применить решение для нескольких сил.

В первом приближении. Рассмотрим движение при отсутствии сил сопротивления.

M+CU=P

+++…=0

+++…=0

……………………………………………….. (a)

+++…=

………………………………………………..

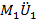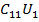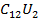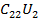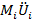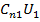+++…=0

Имеем систему д.у. 2-го порядка с постоянными коэффициентами.

В общем случае решение будет складываться из свободных колебаний с собственными частотами и вынужденных колебаний с частотой возмущения.

Т.к. свободные колебания через некоторое время затухают, то возн. установ-ся пр-сс вынужденных колебаний с частотой возмущающей силы, => в установившемся режиме задачей исследования является определение амплитуд колебаний системы по формулам:

=

=

…………………. (б)

=

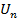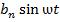
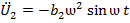
(в)

…………………………….

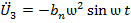
После двукратного дифференцирования, приведения подобных членов, и сокращения:

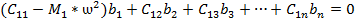
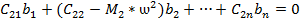
……………………………………………………………………………………. (г)

……………………………………………………………………………………

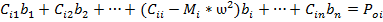
Получили неоднородную систему алгебраических уравнений относительно амплитуд перемещений.

Для решения воспользуемся методом определителей, по формулам Крамера.

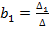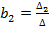; ;….;; (д)

(е) ∆= ……………………………

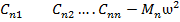
(ж) = ……………………………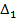

…………………………..

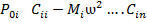
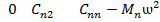
По теореме Безу определитель

(е) можно представить в виде:

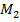∆=*….. (з)

Где - собственные частоты заданной системы.

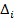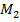=*….. (и)

- парциальные собственные частоты рассматриваемой системы, если на i-тый инертный элемент наложить связь, препятствующую перемещению.

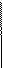Подставляя (з) и (и) в (д), получим.

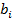=(74)

Проанализируем выражение (74)

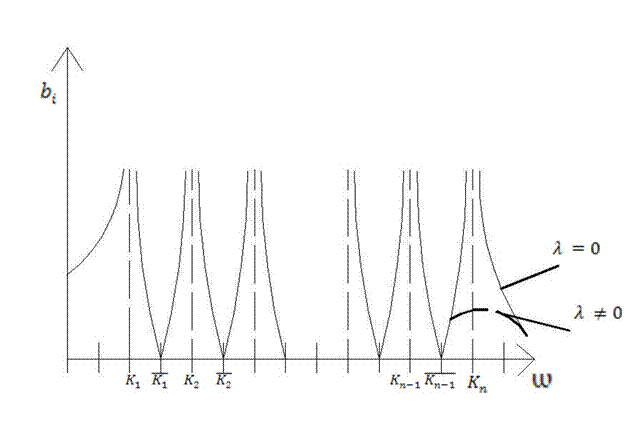
Зависимость амплитуды от частоты колебаний.

При приближении частоты возмущения к собств. ч-те заданной системы амплитуда колебаний возрастает.

При отсутствии сопряжения возрастает до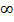

При приближении ѡ - частоты возмущения к парц. ч-те 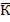амплитуда колебаний обращается в нуль.

При учете трения резонансные явления не приводят к бесконечному возрастанию амплитуд колебаний.

Наиболее сильно резонанс развивается на низших собств. частотах системы.

При учете сил сопряжения, эффект уменьшения амплитуд колебаний до нуля снижается.

Это явление положено в основу мероприятий по колебаний, которое называется Виброгашением.

Дата добавления: 2014-01-06