Лекция 2. Геометрическая интерпретация решения задач линейного программирования

План

1. Геометрический смысл задачи линейной оптимизации.

2. Алгоритм графического решения задач ЛП.

1. Пусть дана задача ЛП:

Z = c 1 x 1 + c 2 x 2 + ⋅⋅⋅ + cn xn → max, (1)

+ a x + ⋅⋅⋅ + a x ≤ b

⎧ a 11 x 1 + a 12 x 2 + ⋅⋅⋅ + a 1 n xn ≤ b 1

⎪

⎪ a 21 x 1 22 2 2 n n 2

⎨

⎪.......................................

⎪⎩ am 1 x 1 + am 2 x 2 + ⋅⋅⋅ + amn xn ≤ bm

(2)

x j ≥ 0 (j =1, n). (3)

Рассмотрим систему ограничений (2) с геометрической точки зрения. Ка-

ждое равенство

a 1 x 1 + a 2 x 2 = b

определяет прямую в пространстве

R. Эта пря-

мая делит координатную плоскость на две полуплоскости, определяемые нера-

венствами

a 1 x 1 + a 2 x 2 ≤ b

и a 1 x 1 + a 2 x 2 ≥ b. Данные полуплоскости содержат

прямую в качестве границы.

Равенство

a 1 x 1 + a 2 x 2 + a 3 x 3 = b

представляет собой плоскость в

R. Эта

плоскость делит пространство на два полупространства, задаваемые неравенст-

вами

a 1 x 1 + a 2 x 2 + a 3 x 3 ≤ b и

a 1 x 1 + a 2 x 2 + a 3 x 3 ≥ b. Граница полупространств –

данная плоскость – принадлежит им.

По аналогии равенство

a 1 x 1 + a 2 x 2 +... + anxn = b

называют гиперплоско-

стью в пространстве

Rn. Это граничная гиперплоскость для полупространств,

определяемых неравенствами. Т.о., система ограничений задачи ЛП (2) содер-

жит m полупространств из пространства

Rn. Если система совместна (имеет

хотя бы одно решение), то она определяет выпуклый многогранник, который является геометрическим образом ОДР. Аналогично с трёхмерным пространст- вом будем считать, что угловыми точками выпуклого многогранника в n - мерном пространстве будут его вершины, образованные пересечением гиперп- лоскостей.

Любая внутренняя и граничная точка ОДР является допустимым решени-

ем задачи. Приравняем целевую функцию к нулю. Тогда уравнение

c 1 x 1 + c 2 x 2 + ⋅⋅⋅ + cn xn = 0

определяет в

Rn гиперплоскость, проходящую через начало координат и пер-

пендикулярную вектору-градиенту

c = (с 1, с 2,..., cn). Направление вектора-

градиента показывает направление возрастания функции (рис. 1).

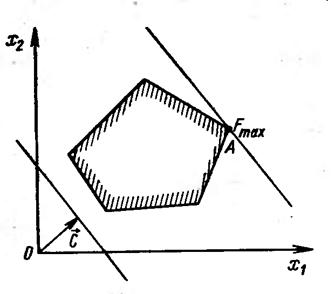
Рис. 1. Графическая иллюстрация задачи ЛП

Поэтому, чтобы найти максимум функции, необходимо передвигать па- раллельными переносами эту гиперплоскость в направлении вектора как можно дальше от начала координат, но чтобы она имела с ОДР хотя бы одну общую точку. Минимум целевой функции достигается в точке ОДР, которая будет ближайшей к началу координат при пересечении с перемещаемой гиперплоско- стью.

2. Пусть задача ЛП содержит только две переменные

x 1 и

x 2:

Z = c 1 x 1 + c 2 x 2 → max, (4)

⎪ + a x ≤ b

⎧ a 11 x 1 + a 12 x 2 ≤ b 1

⎪ a 21 x 1 22 2 2

⎨

⎪.......................

⎩⎪ am 1 x 1 + am 2 x 2 ≤ bm

(5)

x j ≥ 0 (j =1, 2). (6)

Тогда все построения можно выполнить в координатной плоскости и решить

задачу (4)-(6) графически.

Приведём алгоритм графического решения задачи ЛП:

1. Записать уравнения граничных прямых

аi 1 x 1 + аi 2 x 2 = bi

(i =1, m) и построить

их на плоскости

x 1 Ox 2.

2. Определить полуплоскости, которые соответствуют каждому ограничению-

неравенству с помощью контрольной точки.

3. Выделить область допустимых решений (ОДР).

4. Построить вектор

G

c = (с 1 ,с 2)

– направление наибольшего возрастания целе-

вой функции Z:

G

c = (с 1 ,с 2) = grad Z

⎛ ∂Z

= ⎜ ∂ x

, ∂ Z ⎞.

⎟

∂ x

⎝ 1 2 ⎠

5. Построить прямую, перпендикулярную вектору c. Её называют линией

уровня или изоцелью. G

6. Перемещать эту прямую в направлении вектора c, если задача на максимум,

и в противоположном направлении, если задача на минимум, пока она не станет касательной (опорной) к ОДР.

7. Определить координаты оптимальной точки и вычислить оптимальное зна-

чение функции Z.

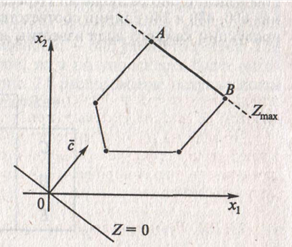
Рассмотрим наиболее типичные ситуации, возникающие при графических решениях задачи ЛП. На рис. 2, А) показано, что в угловой точке A целевая функция достигает максимального значения, а в точке B – минимального.

Рис. 2, Б) отражает случай, когда линия уровня параллельна отрезку AB,

принадлежащему ОДР. Максимум целевой функции достигается в точке A, в

точке B (Z max

= Z (A) = Z (B)) и в любой точке отрезка AB. Поэтому оптималь-

ных решений будет бесконечное множество и все они описываются выпуклой комбинацией точек A и B:

X * = λ(x 1, A; x 2, A) + (1 − λ)(x 1, B; x 2, B) = (λ x 1, A + (1 − λ) x 1, B; λ x 2, A + (1 − λ) x 2, B),

где 0 ≤ λ ≤1.

 

 

А) Б)

Рис. 2. Наличие графического решения задач ЛП

Напомним, что выпуклой линейной комбинацией произвольных n -

n

мерных векторов

X 1, X 2,..., X n

из пространства

R называется сумма

λ1 X 1 + λ2 X 2 +... + λ n X n,

n

где числа

λ j ≥ 0 (j =1, n) и

∑ λ j

j =1

=1.

Заметим, что в пространстве

R 2 выполняется равенство λ + λ

=1. Обо-

значим вид

λ1 = λ, тогда

1 2

λ2 =1 − λ. Поэтому выпуклая линейная комбинация имеет

λ X 1 + (1 − λ) X 2,

где 0 ≤ λ ≤1.

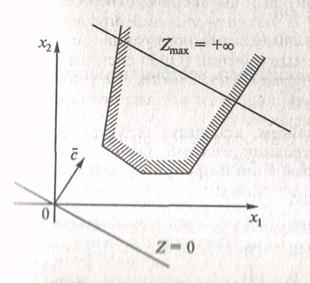
Принципиально другие ситуации рассмотрены на рис. 3. Так рис. 3, А)

изображает вариант, когда система ограничений образует неограниченное сверху множество. Функция Z при этом стремится к бесконечности. На рис. 3,

Б) представлен случай несовместной системы ограничений.

 

А) Б)

Рис. 3. Случаи отсутствия решения задач ЛП

Домашнее задание. Составить четыре конкретные задачи ЛП на мини-

мум, аналогичные ситуациям, рассмотренным на рис. 2 и 3.

Дата добавления: 2014-01-07