Чистых оптимальных стратегий

(i 0, j 0)

первого и второго игроков, соответст-

венно. Седловой элемент

a является минимальным в

i j

0 0

i 0 -й строке и макси-

мальным в

j 0 -м столбце. Игра решена полностью, если в матрице A имеется

седловая точка.

Решение примера 1 методом максимина и минимакса. Справа от мат-

рицы A запишем элементы минимальные по строкам, выберем среди них мак-

симальный и выделим его уголком. Получим, что α = 0, 7.

Под матрицей A запишем элементы максимальные по столбцам, выберем

из них минимальный и выделим его уголком. Имеем

β = 0, 7.

Т.к. α = β, то игра имеет седловую точку. Седловой элемент

деляем квадратом:

a 31 = 0, 7

вы-

⎛ 0, 4 0,8 ⎞

⎜ ⎟

0, 4

A = ⎜

0, 5 0, 9 ⎟

0, 5

⎝ ⎠

⎜ 0, 7 0,8 ⎟

0, 7 0, 9

.

0, 7

Ответ: чистой оптимальной стратегией для первого игрока будет 3-я

стратегия, для второго – 1-я, чистая цена игры составит V * = 0, 7.

3. Отметим, что далеко не все платёжные матрицы имеют седловые точки. Сле-

довательно, не каждая матричная игра имеет оптимальные чистые стратегии.

Пример 2 (планирование структуры посевных площадей). Пусть аг-

рарное предприятие (первый игрок) может посеять одну из двух сельскохозяй-

ственных культур (i =1,2). Состояние экономической среды (стратегии второго

игрока) определяется погодными условиями: 1) год засушливый; 2) год нор-

мальный; 3) год дождливый (j =1, 2, 3). Информация о выигрышах первого иг-

рока помещена в табл. 2.

Табл. 2. Доход от реализации (млн. грн.)

	Второй игрок (погода)
Сухая погода	Нормальная погода	Дождливая погода
Первый игрок (аграрное пред- приятие)	1-я культура
2-я культура

Платёжная матрица имеет вид:

⎛1 3 4 ⎞

A = ⎜ ⎟.

⎝ 4 3 2 ⎠

Для определения чистых стратегий игроков применим метод максимина и

минимакса:

⎛1 3 4 ⎞ 1

A = ⎜ ⎟

⎝ 4 3 2 ⎠ 2.

4 3 4

Нижняя чистая цена игры

α = 2. Верхняя чистая цена игры

β = 3. Числа

α и β не совпадают. Седловой точки нет. Следовательно, чистые оптимальные

стратегии для игроков не существуют. Чистую цену игры V *

возможно.

определить не-

Вернёмся к рассмотрению общих вопросов. Как поступать, если платёж-

ная матрица

⎛ a 11

a 12

...

a 1 n ⎞

⎜ ⎟

A = ⎜ a 21

a 22

...

a 2 n ⎟

⎜............ ⎟

⎜ ⎟

⎝ am 1

am 2

...

amn ⎠

не содержит седловой точки и чистых оптимальных стратегий нет?

В этом случае применяют не чистые, а смешанные стратегии. Т.е. первый игрок применяет свои m стратегий с определёнными вероятностями. Вектор вероятностей X неизвестен:

X = (x 1; x 2;...; xm),

x 1 + x 2 +... + xm =1.

Аналогично, для второго игрока неизвестен вектор вероятностей Y, с ко-

торыми он принимает свои стратегии:

Y = (y 1; y 2;...; yn),

y 1 + y 2 +... + yn =1.

Векторы X и Y называются смешанными стратегиями первого и вто- рого игроков, соответственно. Координаты этих векторов (вероятности) опре- деляют на основе статистических данных, т.е. эмпирическим путём. Поэтому данный раздел математики называют теорией игр и статистических решений.

Теорема 2 (основная теорема матричных игр фон Неймана). Любая матричная игра двух лиц с нулевой суммой имеет решение в виде смешанных

стратегий.

Для того чтобы найти оптимальные смешанные стратегии X и Y, а также определить неизвестную цену игры V, используют следующую теорему.

Теорема 3 (о свойствах оптимальных смешанных стратегий). Пусть задана игра с известной платёжной матрицей A и неизвестной ценой V. Для

того чтобы вектор

X = (x 1; x 2;...; xm)

был оптимальной смешанной стратегией

первого игрока, необходимо и достаточно выполнение условий:

x 1 + x 2 +... + xm =1, (1)

⎪ a 12 x 1 22 2 m 2 m

⎧ a 11 x 1 + a 21 x 2 +... + am 1 xm ≥ V,

⎪ + a x +... + a x ≥ V,

⎨

⎪........................................

⎪⎩ a 1 nx 1 + a 2 n x 2 +... + amn xm ≥ V,

(2)

xi ≥ 0

(i =1, m). (3)

Аналогично для второго игрока: чтобы вектор

Y = (y 1; y 2;...; yn)

был опти-

мальной смешанной стратегией второго игрока, необходимо и достаточно вы-

полнение условий:

y 1 + y 2 +... + yn =1, (4)

⎪ a 21 y 1 22 2 2 n n

⎧ a 11 y 1 + a 12 y 2 +... + a 1 n yn ≤ V,

⎪ + a y +... + a y ≤ V,

⎨

⎪........................................

⎪⎩ am 1 y 1 + am 2 y 2 +... + amn yn ≤ V,

(5)

y j ≥ 0

(j =1, n). (6)

Рассмотрим применение теоремы 3 при условии, что все элементы пла-

тёжной матрицы A положительные. Тогда

V > 0

и на это число можно разде-

лить левые и правые части условий задачи (1)-(3):

x 1 + x 2

+... + xm

= 1, (7)

V V V V

⎧ a ⋅ x 1 + a

⋅ x 2

+... + a

⋅ xm

≥1,

⎪ 11 V

⎪

21 V

m 1 V

⎪ a ⋅ x 1 + a

⋅ x 2

+... + a

⋅ xm

≥1,

⎨

12 V

22 V

m 2 V

(8)

⎪........................................

⎪

⎪ a ⋅ x 1 + a

⋅ x 2 +... + a

⋅ xm

≥1,

1 n V

2 n V

mn V

xi ≥ 0 (i =1, m). (9)

V

Введём замену переменных:

t = x 1, t

= x 2,..., t

= xm, Z =

1. Т.к. первый

1 V 2 V

m V V

игрок стремится максимизировать цену игры, то

V → max, а значит

Z → min.

Задача (7)-(9) примет вид задачи линейного программирования (ЛП):

Z = t 1 + t 2 +... + tm → min, (10)

⎪ a 12 t 1 22 2 m 2 m

⎧ a 11 t 1+ a 21 t 2 +... + am 1 tm ≥1,

⎪ + a t +... + a t ≥1,

⎨

⎪........................................

⎪⎩ a 1 nt 1 + a 2 nt 2 +... + amntm ≥1,

(11)

ti ≥ 0

(i =1, m). (12)

Аналогично для второго игрока. Сделаем замену переменных в задаче (4)-

(6): w

= y 1, w

= y 2,..., w

= yn, F =

1. Будет получена вторая задача ЛП:

1 V 2 V

n V V

F = w 1 + w 2 +... + wn → max, (13)

⎪ a 21 w 1 22 2 2 n n

⎧ a 11 w 1+ a 12 w 2 +... + a 1 nwn ≤1,

⎪ + a w +... + a w ≤1,

⎨

⎪........................................

⎪⎩ am 1 w 1+ am 2 w 2 +... + amnwn ≤1,

(14)

w j ≥ 0

(j =1, n). (15)

Заметим, что задачи (10)-(12) и (13)-(15) являются двойственными отно- сительно друг друга. Для их решения можно применять симплекс-метод, метод искусственного базиса и в задачах малой размерности – графический метод.

Решение примера 2. Ранее мы доказали, что платёжная матрица

⎛1 3 4 ⎞

A = ⎜ ⎟

⎝ 4 3 2 ⎠

не имеет седловой точки и чистых оптимальных стратегий для этой задачи не

существует.

Согласно теореме 2 применим смешанные стратегии. Вектор вероятно-

стей X первого игрока неизвестен:

X = (x 1; x 2),

x 1 + x 2 =1.

Аналогично, для второго игрока неизвестен вектор вероятностей Y, с ко-

торыми он принимает свои стратегии:

Y = (y 1; y 2; y 3),

y 1 + y 2 + y 3 =1.

Применим теорему 3. Цена игры V является неизвестной. Для того чтобы

вектор

X = (x 1; x 2)

был оптимальной смешанной стратегией первого игрока, не-

обходимо и достаточно выполнение условий:

x 1 + x 2 =1, (16)

⎧ x 1 + 4 x 2 ≥ V,

⎪

⎪

⎨3 x 1+ 3 x 2 ≥ V,

⎩4 x 1+ 2 x 2 ≥ V,

(17)

xi ≥ 0

(i =1, 2). (18)

Аналогично для второго игрока: чтобы вектор

Y = (y 1; y 2; y 3)

был опти-

мальной смешанной стратегией второго игрока, необходимо и достаточно вы-

полнение условий:

y 1 + y 2 + y 3 =1, (19)

⎧ y 1 + 3 y 2 + 4 y 3 ≤ V,

⎨

⎩4 y 1 + 3 y 2 + 2 y 3 ≤ V,

(20)

y j ≥ 0

(j =1, 3). (21)

Введём замену переменных: t

= x 1, t

= x 2, Z =

1. Задача (16)-(18) примет

вид задачи ЛП:

1 V 2 V V

Z = t 1 + t 2 → min, (22)

⎧ t 1 + 4 t 2 ≥1,

⎪

⎪

⎨3 t 1+ 3 t 2 ≥1,

⎩4 t 1+ 2 t 2 ≥1,

(23)

ti ≥ 0

(i =1, 2). (24)

Аналогично для второго игрока. Сделаем замену переменных в задаче

(19)-(21): w

= y 1, w

= y 2, w

= y 3, F =

1. Будет получена вторая задача ЛП:

1 V 2 V

3 V V

F = w 1 + w 2 + w 3 → max, (25)

⎧ w 1+ 3 w 2 + 4 w 3 ≤1,

⎨

⎩4 w 1+ 3 w 2 + 2 w 3 ≤1,

(26)

w j ≥ 0

(j =1, 3). (27)

Т.к. задача (22)-(24) содержит две переменных, то ёё удобно решить гра-

фически (студентам проделать самостоятельно). Оптимальный план единствен-

ный: T * = ⎛

2; = 3 ⎞, Z = 5.

⎝ ⎠

⎜14 14 ⎟

min 14

Задачу (25)-(27) можно решить симплекс-методом (студентам проделать самостоятельно). Однако удобнее воспользоваться первой и второй теорема- ми двойственности.

Т.к.

Z min = F max, то

w + w + w = 5. Оптимальные значения

1 2 3 14

t * = 2 и

1 14

t 2* = 14

строго больше нуля, поэтому 1-е и 2-е ограничения в системе (26) бу-

дут строгими равенствами. В итоге, для решения задачи (25)-(27) достаточно

решить систему уравнений (студентам проделать самостоятельно):

⎧ w + w

+ w = 5,

⎪ 1 2 3 14

⎪

⎨ w 1+ 3 w 2 + 4 w 3 =1,

⎪4 w + 3 w + 2 w =1.

⎪ 1 2 3

⎩

Однако, лучше всего, дополнительно учесть тот факт, что при

t * = 2 и

1 14

t 2* = 14

в системе (23) 1-е и 3-е ограничения обратятся в строгие равенства, а 2-

е – в неравенство. Следовательно,

приобретёт вид:

w 1* > 0

и w 3* > 0, а

w 2* = 0. Т.о. система (26)

⎧ w 1+ 4 w 3 =1,

⎨

⎩4 w 1+ 2 w 3 =1.

Решая систему, придём к оптимальному плану:

⎝ ⎠

W * = ⎛

2; 0; = 3 ⎞,

F = 5. Т.е. задачи ЛП (22)-(24) и (25)-(27) решены полностью.

max 14

1

⎜14 14 ⎟

Выполним обратную замену

y 1 = w 1 V, y 2 = w 2 V, y 3 = w 3 V.

V =, x 1 = t 1 V, x 2 = t 2 V и

Z

Ответ: оптимальной смешанной стратегией для первого игрока будет

X * = (0, 4; 0, 6), для второго –

V * = 2,8.

Y * = (0, 4; 0; 0, 6), чистая цена игры составит

Значит, аграрному предприятию следует под 1-ю сельскохозяйственную культуру отвести 40% земли, под 2-ю – 60%. При этом гарантированный доход от реализации продукции составит 2,8 млн. грн.

4. Рассмотрим несколько полезных фактов из теории игр.

Пусть для i -й и k -й стратегий первого игрока выполняются соотношения

aij ≥ akj

(j =1, n),

причём хотя бы одно из них является строгим неравенством. Т.е. элементы i -й строки больше либо равны элементов k -й строки. Тогда говорят, что стратегия i превосходит или доминирует стратегию k. Т.к. первый игрок заинтересован в увеличении своего выигрыша, то его доминирующая стратегия i предпоч- тительнее стратегии k.

Пусть теперь для j -й и r -й стратегий второго игрока выполняются соот-

ношения

aij ≥ air

(i =1, m),

причём хотя бы одно из них является строгим неравенством. Т.е. элементы j - го столбца больше либо равны элементов r -го столбца. Значит у второго игро- ка стратегия j доминирует стратегию r. Т.к. второй игрок заинтересован в

уменьшении выигрыша первого игрока, то его r -я стратегия предпочтительнее

j -й стратегии.

Замечание 1. Наличие доминирующих стратегий позволяют снизить раз- мерность матрицы игры A и, тем самым, уменьшить объём вычислений при нахождении смешанных стратегий.

Пример 3. Игра двух лиц с нулевой суммой задана матрицей:

⎛ 4 3 5 1 ⎞

⎜ 4 5 3 5 ⎟

A = ⎜ ⎟.

⎜5 3 5 3 ⎟

⎝ ⎠

⎜1 5 4 8 ⎟

Для определения чистых стратегий игроков применим метод максимина и

минимакса:

⎛ 4 3 5 1 ⎞ 1

⎜ 4 5 3 5 ⎟ 3

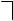A = ⎜ ⎟

⎜5 3 5 3 ⎟ 3.

⎜ ⎟

⎝1 5 4 8 ⎠ 1

5 5 5 8

Нижняя чистая цена игры

α = 3. Верхняя чистая цена игры

β = 5. Числа

α и β не совпадают. Седловой точки нет. Следовательно, чистые оптимальные

стратегии для игроков не существуют. Чистую цену игры V *

возможно.

определить не-

Предположим, что неизвестная цена игры равна V, и будем искать реше- ние игры в смешанных стратегиях. Пусть для первого игрока – это неизвестный вектор вероятностей X:

X = (x 1; x 2; x 3; x 4),

x 1 + x 2 + x 3 + x 4 =1.

Аналогично, для второго игрока:

Y = (y 1; y 2; y 3; y 4),

y 1 + y 2 + y 3 + y 4 =1.

Проверим матрицу A на наличие доминирующих стратегий. Сравнивая выигрыши построчно, видим, что у первого игрока 3-я стратегия доминирует 1- ю. Следовательно, для первого игрока 3-я стратегия предпочтительнее 1-й.

В теории игр доказано, что можно в матрице A вычеркнуть 1-ю строку,

положив

x 1 = 0. Будет получена матрица игры:

⎛ 4 5 3 5 ⎞

⎜ ⎟

⎝ ⎠

A 1 = ⎜5 3 5 3 ⎟.

⎜1 5 4 8 ⎟

У новой матрицы

V.

A 1 цена игры будет такой же, как и у матрицы A, т.е. равна

По элементам матрицы

A 1 видно, что у второго игрока 4-я стратегия до-

минирует 2-ю. Т.о. 2-я стратегия второго игрока предпочтительнее его 4-й стра-

тегии. Следовательно, в матрице

y 4 = 0:

A 1 можно вычеркнуть 4-й столбец, положив

⎛ 4 5 3 ⎞

⎜ ⎟

⎝ ⎠

A 2 = ⎜5 3 5 ⎟.

⎜1 5 4 ⎟

Цена игры останется прежней, т.е. V.

В матрице

A 2 доминирующих стратегий нет. Т.о. исходную игру с мат-

рицей A размерности 4 × 4

3 ×3.

удалось свести к игре с матрицей

A 2 размерности

На данный момент смешанные стратегии игроков для исходной задачи имеют вид:

X = (0; x 2; x 3; x 4),

Y = (y 1; y 2; y 3; 0).

Далее, используя матрицу

A 2, применяем теорему 3. Составляем двойственные

задачи ЛП (10)-(12) и (13)-(15). Находим оптимальные значения вероятностей

x 2*, x 3*, x 4 * и стоятельно).

y 1*, y 2*, y 3 *, а также цену игры V *

(студентам проделать само-

Теорема 4. Пусть задана игра двух лиц с матрицей

VA. Тогда другая игра с матрицей

A = (aij)

и ценой игры

B = (bij) = (c ⋅ aij + d),

c > 0,

будет иметь оптимальные смешанные стратегии игроков такие же, как и для

игры с матрицей ношением:

A = (aij). Причём цена игры VB

VB = c ⋅ VA + d.

связана с ценой игры VA

соот-

Замечание 2. Пользуясь теоремой 4, можно упрощать элементы исходной матрицы A для облегчения вычислений.

Пример 4. Рассмотрим игру с матрицей

⎛300 400 ⎞

A = ⎜ ⎟.

⎝700 200 ⎠

Для определения чистых стратегий игроков применим метод максимина и

минимакса:

⎝ ⎠

A = ⎛300 400 ⎞

⎜700 200 ⎟

700 400

200.

Нижняя чистая цена игры

α = 300. Верхняя чистая цена игры

β = 400.

Числа α и β не совпадают. Седловой точки нет. Следовательно, чистые опти-

мальные стратегии для игроков не существуют. Чистую цену игры определить

невозможно. Доминирующих стратегий нет.

Воспользуемся теоремой 4. Каждый элемент матрицы A разделим на 100

и вычтем 2. Будет получена матрица

B = (bij) = (0, 01⋅ aij − 2), т.е.

⎛1 2 ⎞

B = ⎜ ⎟.

⎝5 0 ⎠

Смешанные стратегии игроков для матриц A и B совпадают. Обозначим

векторы неизвестных вероятностей через

связаны равенством:

X = (x 1; x 2)

и Y = (y 1; y 2). Цены игр

VB = 0, 01⋅ VA − 2.

Далее, используя матрицу B, применяем теорему 3. Составляем двойст-

венные задачи ЛП (10)-(12) и (13)-(15). Находим оптимальные значения веро-

ятностей и цену игры VB * (студентам проделать самостоятельно).

Окончательно получим:

V * = VB * +2 =100 ⋅ (V

* +2).

A 0, 01 B

Завершая данную лекцию, отметим, что игровые методы активно исполь- зуются при изучении экономических рисков. Для нахождения статистических решений применяются критерии Байеса, Бернулли, Лапласа, Вальда, Сэвиджа, Гурвица и др.

ЛИТЕРАТУРА

1. Акулич И.Л. Математическое программирование в примерах и задачах. –

М.: Высш. шк., 1986. – 319 с.

2. Афанасьев М.Ю., Суворов Б.П. Исследование операций в экономике: мо-

дели, задачи, решения. – М.: ИНФРА-М, 2003. – 444 с.

3. Глухов В.В., Медников М.Д., Коробко С.Б. Математические методы и модели для менеджмента. – СПб.: Издательство «Лань», 2007. – 528 с.

4. Иванов С.Н. Математические методы исследования операций. – Донецк:

Донецкий национальный университет, 2003. – 688 с.

5. Костевич Л.С. Математическое программирование: информационные технологии оптимальных решений. – Мн.: Новое знание, 2003. – 424 с.

6. Кузнецов А.В., Сакович В.А., Холод Н.И. Высшая математика: математи-

ческое программирование. – Мн.: Выш. шк., 1994. – 286 с.

7. Таха Х.А. Введение в исследование операций. – М.: Издательский дом

«Вильямс», 2005. – 912 с.

8. Христиановский В.В., Ерин В.Г., Ткаченко О.В. Решение задач математи-

ческого программирования. – Донецк: ДонГУ, 1992. – 254 с.

9. Христиановский В.В., Полшков Ю.Н., Щербина В.П. Экономический риск и методы его измерения. – Донецк: ДонГУ, 1999. – 250 с.

10.Вітлінський В.В., Верченко П.І., Сігал А.В., Наконечний Я.С. Еко-

номічний ризик: ігрові моделі. – К.: КНЕУ, 2002. – 446 с.

11.Нейман Дж. Теория игр и экономическое поведение: Монография / [Дж.

фон Нейман, О. Моргенштерн]. – М.: Наука, 1970. – 707 с.: ил., табл. –

Библиогр.: с. 695–702.

12.Крушевский А.В. Теория игр: Учеб. пособие / [А. В. Крушевский]. – К.:

Вища школа, 1977. – 216 с.: ил., табл. – Библиогр.: с. 214.

13.Вітлінський В.В., Наконечний С.І. Ризик у менеджменті. – К.: ТОВ “Бо-

рисфен-М”, 1996. – 336 с.

14.Дубров А.М., Лагоша Б.А., Хрусталев Е.Ю. Моделирование рисковых си-

туаций в экономике и бизнесе. – М.: Финансы и статистика, 1999. – 176 с.

15.Первозванский А.А., Первозванская Т.Н. Финансовый рынок: расчет и риск. – М.: ИНФРА-М, 1994. – 192 с.

16.Полшков Ю.Н. Экономический риск и методы его измерения. / Методи-

ческие указания к выполнению контрольных работ. – Донецк: ДИП, 2001.

– 35 с.

17.Полшков Ю.Н. Актуарные и финансовые расчеты. / Методические указа-

ния и задания к выполнению контрольных работ. – Донецк: ДИП, 1997. –

23 с.

18.Христиановский В.В., Щербина В.П., Медведева М.И., Флетчер Э. Прак-

тикум по прогнозу и риску. – Донецк: ДонНУ, 2000. – 316 с.

19.Шарп У., Александер Г., Бэйли Дж. Инвестиции: Пер. с англ. – М.:

ИНФРА-М, 1999. – XII, 1028 с.

Дата добавления: 2014-01-07