Цепи Маркова. Марковский процесс

Лекция 19.

Одним из простейших случайных процессов является так называемый конечный марковский процесс (конечная марковская цепь).

Для ознакомления с основными понятиями марковских цепей рассмотрим следующий пример.

Пример. Фишка находится на средней клетке в ряду из пяти клеток A, B, C, D, E, считая слева направо, и перемещается на соседнюю клетку по правилу: если она не на крайней клетке, то перемещается вправо, когда выпадет герб (Г) при подбрасывании монеты, и влево, когда выпадет решетка (Р); если фишка на крайней клетке, то остается на ней независимо от выпадения Г или Р.

При первом подбрасывании монеты в зависимости от выпадения Г или Р фишка переместится на одну клетку вправо или влево соответственно. При следующем подбрасывании монеты новое положение фишки будет зависеть только от предыдущего ее местоположения (состояния), то есть фишка может оказаться либо с краю, либо опять в игре.

Итак, всякое новое положение фишки при очередном подбрасывании монеты зависит только от ее предыдущего состояния (местоположения).

Пусть 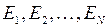– множество состояний некоторой физической системы, и пусть в различные дискретные моменты времени 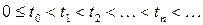. физическая система принимает одно из состояний 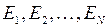. Для математического описания эволюции системы введем последовательность случайных величин 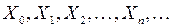. При этом если в момент времени 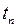система находилась в состоянии 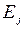, то будем считать, что . Таким образом, нижний индекс случайной величины 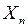указывает на то, в какой отсчет времени рассматривается состояние системы, а сама случайная величина 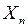принимает значения 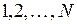номера состояния системы.

Определение. Последовательность 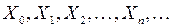называется цепью Маркова с состояниями 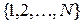, если

, ,

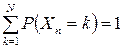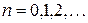и для любого 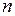и любых 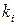, 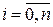таких, что 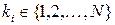, справедливо равенство

.

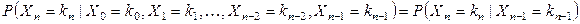Из этого определения следует, что в случае цепи Маркова для любого 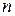вероятность перехода физической системы в некоторое состояние в отсчет времени 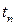зависит от того, в каком состоянии она находилась в отсчете времени , но не зависит от состояний системы в предыдущие моменты времени. Иначе, при фиксированном настоящем будущее системы не зависит от прошлого.

Определение. Цепь Маркова 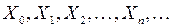называется однородной, если при любых 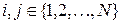вероятности

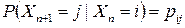
не зависят от .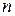

Рассмотренный пример иллюстрирует однородную цепь Маркова. Однородные цепи Маркова характеризуются тем, что вероятности перехода 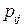из состояния 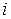в состояние 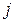не зависят от того, в какой отсчет времени 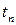рассматривается этот переход, то есть не зависят от номера 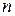шага процесса. В дальнейшем будем рассматривать только однородные цепи Маркова.

Вероятности перехода 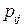представляют в виде матрицы

.

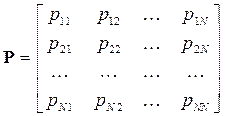Матрица 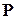называется матрицей перехода или стохастической матрицей. Элементы матрицы 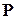имеют следующие свойства.

1⁰. , .

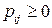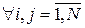2⁰ , .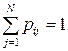

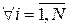Для полного описания вероятностных свойств марковской цепи вводят, кроме стохастической матрицы 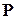, вектор начальных вероятностей

,

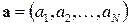где 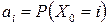, , 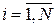то есть 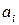– вероятность того, что в начальный момент времени 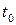физическая система примет состояние .

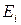Вектор начальных вероятностей 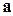и стохастическая матрица 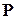определяют совместное распределение случайных величин 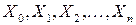при любом 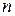. В самом деле, применяя формулу (1.6.4), получаем

.

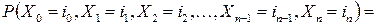
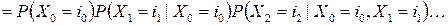
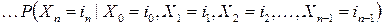Поскольку последовательность случайных величин 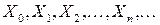образует цепь Маркова, то из последнего равенства находим совместное распределение случайных величин :

.

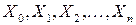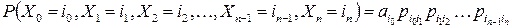По формуле (5.4.2) можно найти вероятность прохождения физической системы через состояния 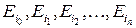соответственно в моменты времени .

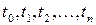Вычислим вероятность перехода системы в состояние 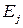в момент времени 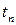. Для искомой вероятности 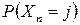можно записать

.

Следовательно,

,

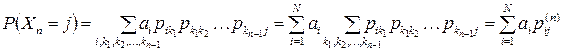то есть

, ,

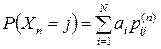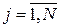где 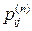– элемент матрицы .

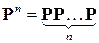Вычислим теперь вероятность перехода за 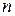шагов. Пусть физическая система находилась в состоянии 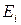в момент времени 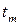. Подсчитаем вероятность того, что в момент времени 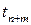система будет находиться в состоянии 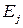, то есть вычислим вероятность 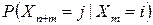. Очевидно, что в случае однородной цепи Маркова для любого справедливо равенство

, ,

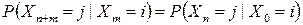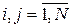то есть вероятность перехода цепи Маркова за 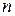шагов не зависит от того, с какого момента времени отсчитываются эти шаги, а зависит только от начального 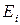и конечного 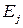состояний системы. Для нахождения вероятности перехода за 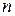шагов достаточно потребовать, чтобы вектор начальных вероятностей имел вид 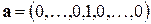, где единица расположены на 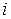-м месте. Тогда искомая вероятность равна

, .

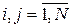Таким образом, матрица 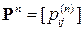полезна как для нахождения вероятности перехода физической системы в состояние 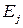, 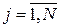в момент времени 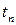, так и для нахождения вероятности перехода за 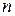шагов.

Определение. Цепь Маркова называется регулярной, если при некотором значении все элементы матрицы 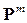положительны.

Теорема. Если цепь Маркова регулярна, то существуют пределы

, ,

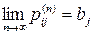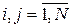которые не зависят от начального состояния 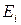, причем 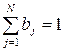, и являются единственным решением системы уравнений

, .

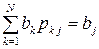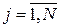Вероятностный смысл данной теоремы состоит в том, что в случае регулярной цепи Маркова вероятность нахождения системы в состоянии 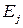с течением времени практически не зависит от того, в каком состоянии она находилась в далеком прошлом. Вектор 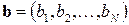называется стационарным распределением вероятности для марковской цепи, а цепь Маркова в этом случае называется эргодической.

Обобщением цепей Маркова являются марковские процессы.

Определение. Процесс 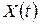, , 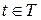называется марковским или процессом без последствия, если при известном значении случайной величины 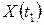значение случайной величины 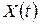, , 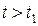не зависит от значения случайной величины , .

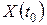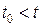Из этого определения следует, что случайный процесс 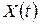является марковским, если для любых 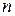моментов времени 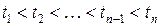из области определения 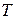случайного процесса 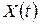, условная функция распределения вероятностей случайной величины 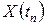при любых допустимых значениях 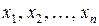соответствующих случайных величин 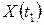, , 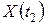…, 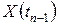имеет вид

.

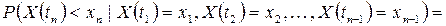
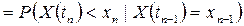Это равенство в терминах условной плотности вероятности случайной величины 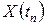означает, что

.

Функция , определяемая данным соотношением, называется условной переходной плотностью вероятности.

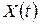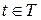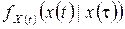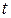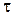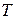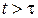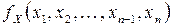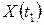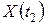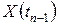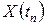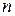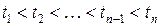Пусть , , – марковский процесс с условной переходной плотностью вероятности , определенной для любых и из , . Пусть – совместная плотность распределения вероятностей случайных величин , , …, , для любых и из 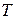. Согласно формуле умножения вероятностей можно записать

.

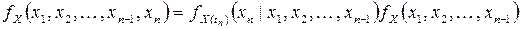Но в силу того, что процесс марковский, имеем

.

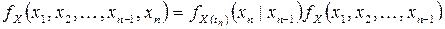Повторив предыдущие рассуждения, найдем

.

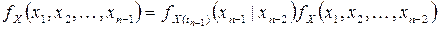Отсюда получаем

.

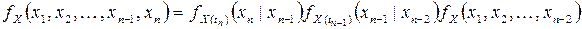Повторив этот процесс 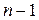раз, окончательно придем к равенству

.

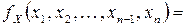
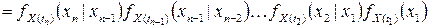Для марковских процессов условные переходные плотности вероятности 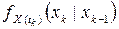, 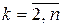обычно известны. Поэтому из равенства (5.5.5) следует, что совместную плотность вероятности марковского процесса можно найти по известной плотности распределения вероятностей .

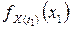Можно показать, что всякий случайный процесс с независимыми приращениями является марковским.

Дата добавления: 2014-01-07