Колебательное движение

Лекция 9

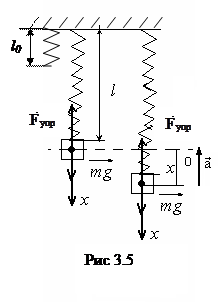
Рассмотрим динамику колебательного движения на примере колебания груза массой m, подвешенного к пружине (рис 3.5). В состоянии равновесия, сила тяжести груза 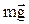уравновешивается силой упругости пружины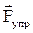

,

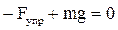F_упр =mg,

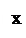где F_упр = kΔl (закон Гука), Δl=l-l₀ , l₀ – длина пружины без груза.

Выведем груз из положения равновесия и дадим ему возможность двигаться вдоль оси Х. Под действием сил тяжести и упругости 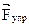груз будет совершать движение с ускорением а согласно уравнениям:

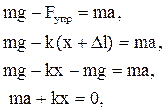
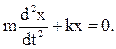(3.12)

Введём обозначение 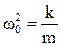, тогда

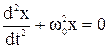. (3.13)

Равенство (3.13) называется дифференциальным уравнением свободных колебаний. Координата смещения груза относительно его положения равновесия, определяется из уравнения (3.13) и равна

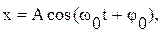(3.14)

где А – амплитуда (максимального смещения груза от положения равновесия),

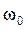- циклическая частота, 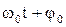- фаза колебания,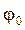- начальная фаза колебания.

Период колебания

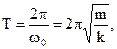(3.15)

частота 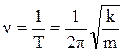. (3.16)

3.3.1 Затухающие колебания

Если груз колеблется в среде, то он испытывает ее сопротивление.

При малых смещениях груза от положения равновесия сила сопротивления

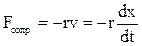, (3.17)

где r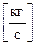– коэффициент сопротивления.

С учетом силы сопротивления дифференциальное уравнение движения груза имеет вид

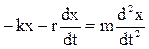. (3.18)

Разделим обе части уравнения (3.18) на m, перенесем все слагаемые в левую часть и введем обозначения 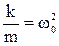,,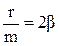 тогда

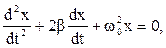(3.19)

где - коэффициент затухания.

В результате решения дифференциального уравнения (3.19) координата смещения груза

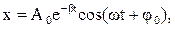(3.20)

где 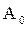и 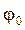- амплитуда колебаний и фаза в момент времени t=0,

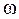- циклическая частота затухающих колебаний (рис 3.7).

Затухающие колебания не являются гармоническими, так как амплитуда этих колебаний убывает по экспоненциальному закону

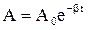. (3.21)

Циклическая частота ω и период Т затухающих колебаний определяются из соотношений:

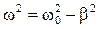, (3.22)

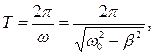(3.23)

где ω₀ частота свободных колебаний тела.

Период определённый из последнего соотношения называется условным периодом затухающих колебаний.

Условный период затухающих колебаний – наименьший промежуток времени Т, за который груз дважды проходит через положение равновесия, двигаясь в одном и том же направлении.

Период затухающих колебаний больше периода свободных колебаний.

Отношение двух амплитуд затухающих колебаний в моменты времени t и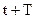

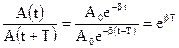(3.24)

называется декрементом затухания. Натуральный логарифм этого отношения называется логарифмическим декрементом

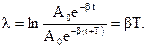(3.25)

Логарифмический декремент затухания характеризует затухание колебаний за период, а коэффициент затухания за единицу времени.

Время, в течение которого амплитуда колебаний уменьшается в е раз называется временем релаксации τ.

,

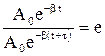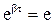
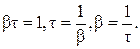(3.26)

Коэффициент затухания – это величина, обратная времени релаксации и определяет число колебаний за единицу времени.

За время τ система совершит 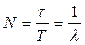колебаний.

Логарифмический декремент затухания равен обратному числу колебаний, совершаемых системой за время релаксации.

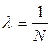(3.27)

3.3.2. Вынужденные колебания и резонанс

Если на груз, кроме упругой силы и силы сопротивления, будет действовать внешняя периодическая сила, то он будет совершать вынужденные колебания.

При внешней силе 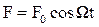дифференциальное уравнение вынужденных колебаний имеет вид

, (3.28)

где 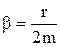- коэффициент затухания; 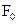- максимальное значение силы;

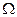- частота изменения силы.

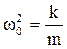- циклическая частота свободных колебаний;

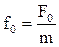- сила, действующая на единицу массы груза.

В результате решения дифференциального уравнения (3.28) координаты смещения груза х = х₁ + х₂,

где 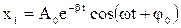- соответствует затухающему колебанию,

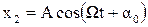- вынужденному.

Затухающие колебания происходят в начальный момент времени и их амплитуда уменьшается с течением времени.

Поэтому в результате действия внешней периодической силы 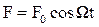долгое время совершаются колебания

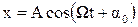(3.29)

где 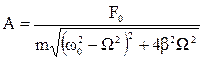, (3.30)

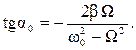(3.31)

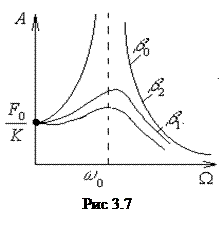
Амплитуда колебаний зависит от частот внешней силы Ω и свободных колебаний ω _0.

Для Ω << ω ₀,

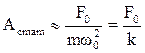, (3.32)

Ω >> ω₀,

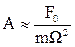, (3.33)

.

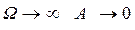Для частоты внешней силы

β₃

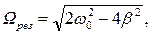(3.34)

наступает резонанс, когда амплитуда максимальна и зависит от коэффициента затухания и частоты свободных колебаний

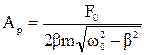(3.35)

Для самостоятельного изучения

3.3.3 Колебания математического маятника

Математический маятник представляет собой материальную точку, подвешенную на невесомой и нерастяжимой нити, например, небольшой шарик, подвешенный на тонкой длинной нити (рис. 3.8). Отклонение маятника от положения равновесия определяется углом 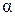. При отклонении маятника от положения равновесия действует момент силы 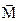, модуль которого равен 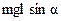, где 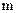- масса шарика;

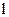- длина нити. Направление момента силы таково, что он стремится вернуть маятник в положение равновесия, т.е. по своему действию момент 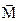аналогичен упругой силе. Поэтому по аналогии с колебанием груза на пружине противоположный знак следует приписать угловому смещению .

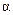Тогда вращательный момент .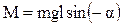

Вращательный момент, действующий на маятник, сообщит маятнику угловое ускорение 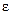. Уравнение движения маятника

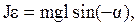(3.36)

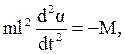
где J=ml²,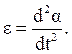

Для малых колебаний =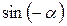

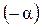
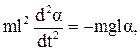(3.37)

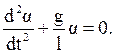
Обозначим 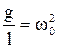и запишем уравнение колебания математического маятника

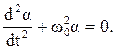(3.38)

Результат решения уравнения (3.38) аналогичен уравнению (3.14) для колебания груза на пружине:

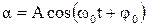(3.39)

Период и частота колебаний математического маятника

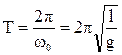, (3.40)

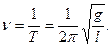(3.41)

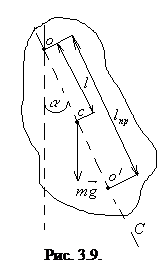Физический маятник

Физический маятник состоит из твёрдого тела, совершающего малые колебания.

При отклонении тела от положения равновесия возникает момент силы тяжести М=mglsinα, где l – расстояние между точкой подвеса О и центром инерции С (рис.3.9).

Уравнения колебаний физического маятника:

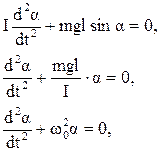(3.42)

где 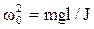, J- момент инерции тела относительно оси, проходящей через точку подвеса О.

Период колебаний физического маятника:

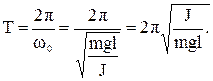
(3.43)

Из сравнения формул (3.43) и (3.40) следует, что математический маятник с приведённой длиной 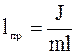и с подвесом в точке О будет иметь такой же период колебаний, как и физический.

Задания для самоконтроля знаний.

1. Определить период и частоту колебаний пружинного маятника с коэффициентом упругости пружины 100 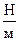и массой груза 10 кг.

2. Определить максимальную скорость колебаний пружинного маятника с параметрами k=200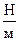, m=5 кг, если максимальное смещение от положения равновесия груза равно 5 см.

3. Определить период затухающих колебаний, если частота свободных колебаний 1 Гц, а коэффициент затухания 2 с^-1.

4. Определить время релаксации затухающих колебаний с коэффициентом затухания 2 с^-1.

5. Определить резонансную частоту колебаний пружинного маятника с коэффициентом упругости 100 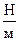, массой груза 10 кг и коэффициентом затухания 2 с^-1.

Дата добавления: 2014-01-07