Геометрический смысл

Понятие дифференциала функции, его свойства и

Лекция 6.2. Понятие дифференциала функции и его применение в приближенных вычислениях

План:

1. Понятие дифференциала функции, его свойства и геометрический смысл

2. Применение дифференциала в приближенных вычислениях

3. Производные и дифференциалы высших порядков

Одним из самых важных понятий дифференциального исчисления наряду с понятием производной, является понятие дифференциала функции. Эти два понятия разные, хотя и тесно связаны друг с другом. Понятие дифференциала первоначально появилось в работах Готфрида Лейбница (1646-1716).

Пусть функция дифференцируема на отрезке .

Как мы знаем, производная функции определяется по формуле:

По теореме о применении бесконечно малых при вычислении пределов

,

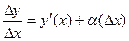где бесконечно малая функция при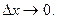

Домножив обе части равенства на 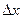, получим

Таким образом, приращение функции представлено в виде суммы двух бесконечно малых слагаемых. Очевидно, что второе слагаемое является бесконечно малой более высокого порядка и при оказывается несущественным и достаточно малым по сравнению с первым. Следовательно, основное влияние на приращение функции оказывает первое слагаемое. Его и называют дифференциалом функции и обозначают .

Дифференциалом функции в точке 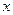называется главная, линейная относительно 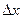, часть приращения функции в этой точке:

(6.1)

Рассмотрим функции Для неё

Таким образом, 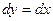, что позволяет переписать формулу дифференциала

(6.2)

Итак, дифференциал функции равен произведению производной функции на дифференциал аргумента. Такая форма записи является общепринятой.

Пример 5… Дана функция 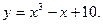Найти в точке при

Решение. Поскольку то Пользуясь равенством 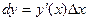, получим

Пример 5.2. Найти дифференциал функции

Решение. В этом примере не указана определенная точка и не дано конкретное приращение 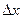. Поэтому, учитывая, что 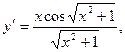получим:

или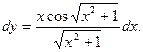

Дифференциал, как и производную можно определить графически.

Геометрический смысл дифференциала

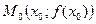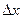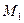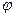Пусть функция в точке имеет производную Проведем к графику этой функции в точке касательную (рис. 28). Дадим значению приращение . Точка на графике функции соответствует значению аргумента Обозначим через угол наклона касательной 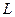к положительному направлению оси Из прямоугольного треугольника имеем 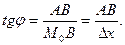То есть

Рис. 28

Как следует из геометрического смысла производной 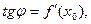поэтому можем записать Получаем, что дифференциал функции в точке равен приращению ординаты касательной 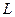проведенной к графику этой функции в точке 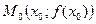, при изменении аргумента от значения к значению

Свойства дифференциала

1) дифференциал функции является линейной функцией от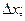

2) дифференциал функции отличается от приращения на величину, которая при условии, что , представляет собой бесконечно малую более высокого порядка, чем т.е.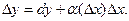

3) Инвариантность формы дифференциала: всегда можно записывать в форме 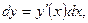независимо от того, является 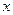независимой переменной или же функция другой переменной.

Правила для вычисления дифференциала

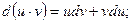
Дата добавления: 2014-01-07