
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекция №5
|
|
|
|
Толқындық теңдеулер
Біртекті изотропты орта алайық және σ = 0, тоқ өткізбейді деген сөз.
Онда Максвеллдың теңдеулурі былай жазылмақ:
 (1)
(1)
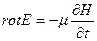 (2)
(2)
 (3)
(3)
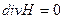 (4)
(4)
Осы теңдеулерді шешіп E немесе H ты табу оңай жұмыс емес. Брақта
Басқа амал бар. Ол үшін ротордан ротор алып көрейік
 (5)
(5)
Бұл текқана математикалық түрлендіру болып саналады.
Максвеллдың бірінші теңдеуінен ротор алайық:
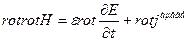 (6)
(6)
Теңдеуде туынды мен ротордың орнын ауыстырайық
 (7)
(7)
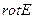 орнына оның мәнін қояйық:
орнына оның мәнін қояйық:
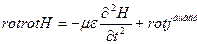 (8)
(8)
Енді (5) мен (8) теңдеулерінің оң жақтарын біріктірейік:
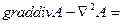
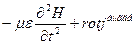 (9)
(9)

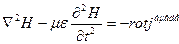 (10)
(10)
Бұл теңдеу толқындық теңдеуі деп аталады.
Егер еске алсақ  фазалық жылдамдық онда
фазалық жылдамдық онда
 (11)
(11)

 Дәл осы әдіспен
Дәл осы әдіспен 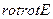 табамыз мынандай теңдеуге шығамыз:
табамыз мынандай теңдеуге шығамыз:

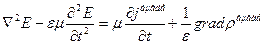 (12)
(12)
Егер толқындық теңдеулердің оң жағы нөлге тең болмаса онда мұдай теңдеулерді Даламбердің текті емес толқындық теңдеулер деп атайды.
Лекция № 6
Электродинамикалық потенциалдар
Максвеллдың 4 ші теңдеуі div B = 0. Егер В орнына rot A алсақ еш нәрсе
де өзгермейді теңдеу нөлге тең болады.
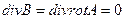 (1)
(1)
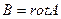 (2)
(2)
 (3)
(3)
 (4)
(4)
Егер А ның орнына А+ 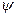 еш нәрсе өзгермейді
еш нәрсе өзгермейді
Максвеллдың екінші теңдеуіне келесі өзгеріс жасайық:
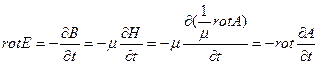 (5)
(5)
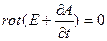 (6)
(6)
Жақшадағы шаманы –gradU деп алайық
 (7)
(7)
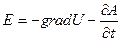 (8)
(8)
Мұнда U- скалярлық потенциал, ал А- векторлық потенциал.
Электр өрісінің кернеулігі мен магнит өрісінің кернеулігі скалярлық және
векторлық потенциал арқылы анықталады. (2) және (8) теңдеулерді
|
|
|
Максвеллдың бірінші теңдеуіне ендірсек мынандай теңдеуге келеміз:
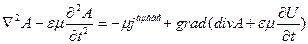 (9)
(9)
(9) шы теңдеуді жеңілдетейік ол үшін жақшаны нөлге теңейік
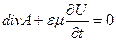 (10)
(10)
Бұл теңдеуді реттеу шарты деп атаймыз.
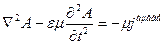 (11)
(11)
Дәл солай U скалярлық потенциал үшін де теңдеу табамыз
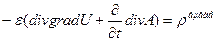 (12)
(12)
Осы теңдеуге реттеу шартын пайдалансақ
 (13)
(13)
Егер Q = Const, онда 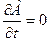
(8) ші теңдеу өзгереді
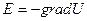 (14)
(14)
Бұл теңдеуді сфералық координат жүйесінде қарастырсақ
(r,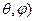
 (15)
(15)
Интеграл алғаннан соң
 (16)
(16)
Егер заряд кішкене көлемде шоғырланған болса
 (17)
(17)
(17) – бұл шешім төмендегі теңдеудің шешімі:
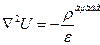 (18)
(18)
Бұл теңдеуді Пуассон теңдеуі деп атайды
Ал енді нүктелі заряд координат басында тұрсын делік және заряд уақытқа тәуелді болсын делік. Онда потенциал U кез келген нүктеде, тек координат басында емес біртекті Даламбер теңдеуіне қанағаттанады
 (19)
(19)
(19) шы теңдеуді шешу үшін сфералық координат жүйнсін r,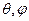 пайдаланған жөн болады (4сурет). Нүктелі заряд координат жүйесінің басында болған соң оның U потенциалы
пайдаланған жөн болады (4сурет). Нүктелі заряд координат жүйесінің басында болған соң оның U потенциалы 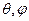 бұрыштарына тәуелді болмайды.
бұрыштарына тәуелді болмайды.
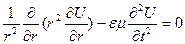 (20)
(20)
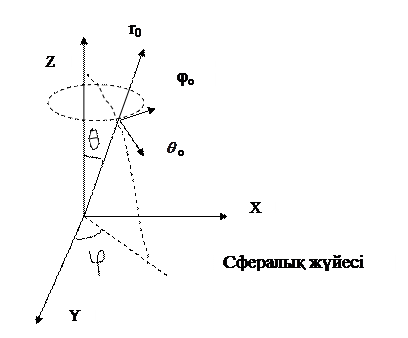
Сурет 4
Егер ескеретін болсақ  және U дан U1 ауыссақ: U1 =rU
және U дан U1 ауыссақ: U1 =rU
 (22)
(22)
(22) – ші теңдеудің жалпы шешімі мынандай түрде беріледі
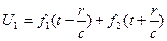 (23)
(23)
 (24)
(24)
Бірінші қосынды бір нүктеден шығып таралатын сфералық толқындарды сипаттайды, ал екінші қосынды бір нүктеге жиналатын сфералық толқындар-
ды сипаттайды.
Нүктелі зарядтардан текқана таралатын сфералық толқындар туындауы мүмкін, ал жиналатын бір нүктеге толқындар шағылу себептен пайда бола алады. Сонымен екінші қосындыны нөлге теңейміз. Потенциал статикалық жағдайда түрі бізге белгілі:
|
|
|
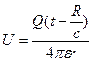 (25)
(25)
Сонымен  (26)
(26)
Егер заряд кішкене көлемде шоғырланған болса
 (27)
(27)
Мұнда  (28)
(28)
 кішкене dV көлемнің декарт координаты
кішкене dV көлемнің декарт координаты
x,y,z- бақылау нүктесі N ның декарт координаты, ал көлем
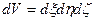 (5 сурет)
(5 сурет)
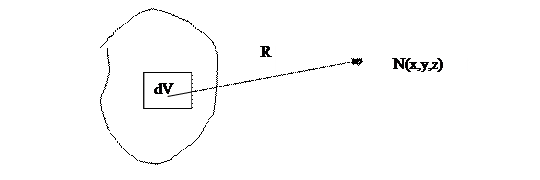
5 сурет
(27) - Даламбер теңдеуінің (13) жеке шешімі.
Дәл солай (11) теңдеуінің жеке шешімі былай болмақ:
 (29)
(29)
Белгілі t- уақытында A, U потенциалдарды табу үшін біз әлде қайда ерте
уақытындағы 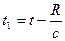 кішкене dV көлемінде тоқ пен зарядты білу керек.
кішкене dV көлемінде тоқ пен зарядты білу керек.
Сол себептен A мен U потенциалдарды кешігетін потенциалдар деп атайды.
Лекция 7
Электрмагнит толқындарының сәуленелуі
Максвеллдің айтуы бойынша диэлектрикте және еркін кеңістікте электр тоғы циркуляция жасай алады бұл тоқты ығысу тоғы деп атаймыз. Ығысу тоғы өткізгіш тоғы сияқты айналасында магнит өрісін тудырады. Бұл өзгеретін магнит өрісі өзгеретін электр өрісін тудырады. Электрмагнит өрістері
бойына энергия ұстап отыралы. Сол себептен қандай болмасын құрылғы кеңістікте ығысу тоғын тудыра алатын болса, онда оны электрмагнит толқындарының сәулеленүші құралы деп санаймыз.
Ең бірінші іске асқан электрмагнит толқындар тарататын құрал ол Герц
вибраторы. Элементарлық электрмагнит вибраторы екі қысқа сымнан тұрады сымдардың бір ұштарына шарлар пісірілген. Екі шарға жоғары жиілікті айнымалы тоқ беріледі. Сол себептен шарлар бір біріне теріс болып зарядталады, ал зарядтар шамасы және белгілері жиілікке сәйкес өзгеріп отырады.
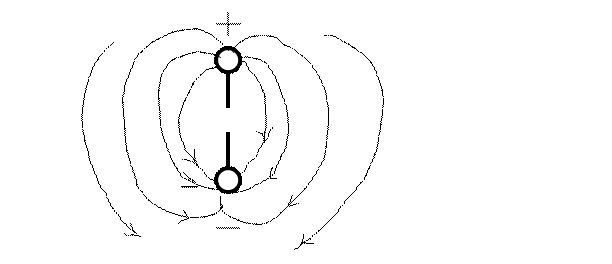
Сурет 1
Кейін электрмагнит толқындарын байланыс ретінде алғаш пайлаланған
А.С. Попов болған.
Элементарлық электр вибраторы (ЭЭВ)
ЭЭВ деп толқынның ұзындығына қарағанда әлде-қайда қысқа тоқ өтетін екі сым фазасы және амплитудасы сым бойымен өзгермейді.
Әрине бұл идеал вибратор осыған жақын келетін Герц вибраторы болып саналады. Вибратор біртекті және изотропты ортада  болсын делік.
болсын делік.
Вибратордағы тоқ белгілі деп санаймыз. Бұл тоқты бөгде тоғы деп санайық себебі осы тоқ арқасында электрмагнит толқындар туады. Вибратор тоғы
|
|
|
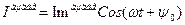 (1)
(1)
Комплекс түрінде 
 (2)
(2)
Біздің мақсатымыз электр және магнит өрістерін табу. Есепті сфералық координат  жүйесінде жүргіземіз. Вибратор өсі Z өсіне орналасқан, ал оның центры координат басымен түйіскен.
жүйесінде жүргіземіз. Вибратор өсі Z өсіне орналасқан, ал оның центры координат басымен түйіскен.
Сурет 2
Вибратордың қима ауданы  , ұзындығы
, ұзындығы 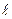 . Интегралды вибратор көлемімен аламыз.
. Интегралды вибратор көлемімен аламыз.
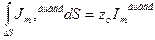 (3)
(3)
Енді векторлық потенциалды былай табамыз:
Am = zo 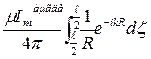 , (4)
, (4)
Мұнда
 (5)
(5)
Интеграл алғанда біз ескеру керекпіз r >> 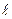 - вибратордан өріс анықтайтын нүктеге дейін – r әлдеқайда вибратор ұзындығынан көп. ЭЭВ дың
- вибратордан өріс анықтайтын нүктеге дейін – r әлдеқайда вибратор ұзындығынан көп. ЭЭВ дың  анықтамасы бойынша r
анықтамасы бойынша r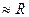 ,
, 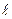 << λ, сол себептен интеграл оңай алынады
<< λ, сол себептен интеграл оңай алынады
 (6)
(6)
Hm векторы Am – векторлы потенциал мен байланысы төмендегі формула
арқылы байланысқан
 (7)
(7)
Em – электр өрісінің кернеулігі былай табылалы:

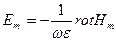 (8)
(8)
Сфералық координат жүйесінде rotA ны алу үшін А векторының  ro,θo,φo орт бағыттарына проекцияларын табу керек. φo орт Z өсіне перпендикуляр жазықтықтығында жатқан соң Z өсімен ro ортжәне θo орт арасында θ және θ +
ro,θo,φo орт бағыттарына проекцияларын табу керек. φo орт Z өсіне перпендикуляр жазықтықтығында жатқан соң Z өсімен ro ортжәне θo орт арасында θ және θ + бұрыш болады. Arm = AzmCosθ; Aφm = - Azm Sin θ; Aφm = 0. Сол себептен Hm вектордың текқана азимуттық құрамасы болады:
бұрыш болады. Arm = AzmCosθ; Aφm = - Azm Sin θ; Aφm = 0. Сол себептен Hm вектордың текқана азимуттық құрамасы болады:
Hm = φo H φm; H φm = 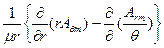 (9)
(9)
Бұл шешімді болжау мүмкін еді, себебі вибратордың түзу тоғының магнит күш сызықтары вибратор өсіне перпендикуляр жазықтығында жатады вибраторды орап. Туындыларды алған соң, тапқанымыз:
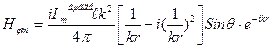 (10)
(10)
Hrm = Hθm = 0. Ал Em векторын табу үшін (8) формуламен пайдаланамыз Hm текқана r, θ ға тәуелді.
Em = 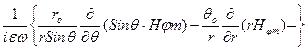 (11)
(11)
Туындыларды тапқан соң
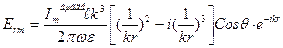 , (12)
, (12)
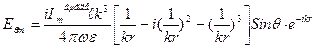 (13)
(13)
Табылған Hm және Em векторларын 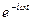 ға көбейтсек толық векторлаын табамыз.
ға көбейтсек толық векторлаын табамыз.
Лекция №8
Элементарлық электр вибраторының алыс, жақын және аралық
|
|
|
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 1412; Нарушение авторских прав?; Мы поможем в написании вашей работы!