Синтез дискретных корректирующих устройств

Структурную схему системы регулирования с ЦВМ можно представить следующим образом. Вне зависимости от сложности решаемых математических задач можно считать, что ЦВМ определяет разность между необходимым значением регулируемой величины и действительным значением, т. е. ошибку 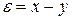. В функции этой ошибки ЦВМ должна прикладывать к системе регулирования управляющее воздействие. Поэтому для исследования динамики следует пользоваться структурной схемой (рис 26.13), в которой ЦВМ условно введена последовательно в цепь вычисления ошибки. В общем случае в контуре регулирования может присутствовать элемент чистого временного запаздывания, выделенный в отдельное звено с передаточной функцией .

Рисунок 26.13. – Структурная схема ЦВМ

Эффекты запоминания на период интегрирования весовой функции (рис.26.14), учитываются также отдельным звеном с передаточной функцией

, .

Если кроме определения ошибки 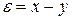ЦВМ производит интегро - дифференциальные операции, то в контуре будет также присутствовать дискретная передаточная функция 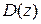, соответствующая некоторому дискретному фильтру, разностное уравнение которого может быть получено из D (z).

Ключи, изображенные на структурной схеме (рис.26.13), генерируют импульсные функции в соответствии с периодом повторения ЦВМ. Проходя через запоминающее устройство (фиксатор нулевого порядка), последовательность импульсных функций образует ступенчатую функцию (рис. 26.14).

В общем случае передаточная функция ЦВМ (рис. 26.13) может быть сделана не равной единице: . Пусть она представляет собой дробно-рациональное выражение вида

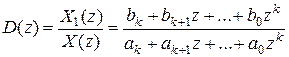
Здесь X (z) и Х ₁(z) - изображения решетчатых функций на входе и выходе ЦВМ.

Степень числителя 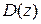не может быть выше степени знаменателя. В формуле 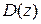взят предельный случай, когда они равны.

После деления числителя и знаменателя на z^k передаточная функция получится в другом виде:

Отсюда можно найти разностное уравнение, соответствующее алгоритму работы ЦВМ:

,

где и - решетчатые функции на входе и выходе ЦВМ.

Результирующая передаточная функция разомкнутой системы:

где W° (z) - передаточная функция разомкнутой системы при D (z) = 1.

Дискретная коррекция может быть также реализована в системах управления без ЦВМ. В этом случае дискретные корректирующие средства реализуются на дискретных фильтрах, построенных на различных ячейках памяти.

Расчет дискретных корректирующих средств, т. е. определение желаемого вида передаточной функции D (z), может производиться следующим образом. Пусть известна желаемая дискретная передаточная функция разомкнутой системы

,

где Ф_ж(z) - желаемая передаточная функция замкнутой системы, a W° (z) - передаточная функция исходной нескорректированной системы. Тогда искомая передаточная функция ЦВМ (или дискретного фильтра) будет

. (26.7)

Формирование желаемой передаточной функции 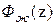необходимо производить с учетом некоторых ограничений. Необходимо, чтобы передаточная функция 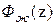содержала в качестве нулей все те нули W° (z), модуль которых равен или больше единицы. Необходимо также, чтобы выражение 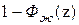содержало в качестве нулей все те полюсы W° (z), модуль которых равен или больше единицы.

Невыполнение этих условий вызывает нарушение требований к грубости системы и вызывает ее неустойчивость, так как приводит к неустойчивым линейным программам ЦВМ, которые должны реализовать получающуюся по формуле (26.7) передаточную функцию D (z).

Кроме того, получающаяся дробно-рациональная передаточная функция D (z) не должна иметь степень числителя выше, чем степень знаменателя, так как это приводит к необходимости знания будущего значения входного сигнала, что не может быть реализовано.

Вместо формулы (26.7) может применяться соотношение, связывающее дискретные частотные передаточные функции

, (26.8)

или соответствующие им логарифмические частотные характеристики

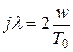После определения подстановкой можно получить передаточную функцию , а затем путем перехода от 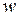-преобразования к z-преобразованию - передаточную функцию .

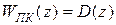Сформулированные выше ограничения по отношению к выражению (26.8) имеют следующий вид. Необходимо, чтобы передаточная функция 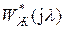содержала в качестве своих нулей и полюсов по переменной все те нули и полюсы передаточной функции , которые лежат в правой полуплоскости. Кроме того, необходимо, чтобы получающаяся дробно-рациональная функция имела степень числителя не больше, чем степень знаменателя.

Поясним сказанное примером. Пусть в цифровой системе с экстраполятором нулевого порядка передаточная функция непрерывной части

соответствует интегрирующему звену второго порядка. Тогда без коррекции имеем

.

Далее можно получить частотную передаточную функцию

Cоответствующая ей ЛАЧХ L построена на рис. 26.15. Если принять в качестве желаемой ЛАЧХ L₁, то желаемая частотная передаточная функция

Она совпадает с типовой передаточной функцией (таблица 26.1), если положить 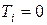, где i = 1, 2,..., n.

Дискретная частотная передаточная функция требуемого корректирующего звена последовательного типа

.

Переход к передаточной функции ЦВМ дает

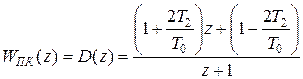
Последнее выражение определяет неустойчивую программу, так как полюс передаточной функции соответствует колебательной границе устойчивости.

Заметим, что получившаяся частотная передаточная функция корректирующего устройства не может быть реализована, вообще говоря, и в непрерывном варианте. Эта функция соответствует бесконечному подъему усиления при росте частоты до бесконечности. При реализации в дискретном варианте эта функция приводит к неустойчивой программе ЦВМ.

Для исключения этого явления примем желаемую ЛАЧХ в другом виде (рис. 26.15). Желаемая передаточная функция

(26.9)

Передаточная функция корректирующего устройства в этом случае имеет вид

Переход к передаточной функции ЦВМ дает

(26.10)

Этой передаточной функции соответствует устойчивая программа ЦВМ.

Рисунок 26.15.

Для рассмотренного примера произведем числовой расчет. Пусть по условиям точности сек^-2, а показатель колебательности М = 1,5.

Базовая частота ЛАЧХ

сек^-1.

Требуемое значение постоянной времени равно

сек.

Допустимое значение суммы малых постоянных времени для передаточной функции (26.9) равно периоду дискретности:

сек.

Примем период дискретности сек. Передаточная функция ЦВМ (26.10) имеет вид

.

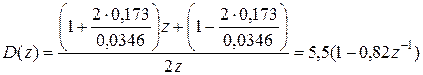В таблице 26.2 приведены некоторые простейшие дискретные корректирующие средства, которые могут реализоваться на ЦВМ или дискретных фильтрах. В таблице 26.2 даны также их параметры и значения модуля частотной передаточной функции на нулевой псевдочастоте и при .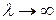

Таблица 26.2.

Дата добавления: 2014-01-07