Комплексне креслення точки

ВСТУП

Механізм забезпечення економічної безпеки національної економіки

Державна діяльність забезпечення економічної безпеки країни передбачає наступні заходи:

• створення інформаційної бази для об'єктивного і всебічного моніторингу економіки й суспільства та його проведення з метою виявлення і прогнозування внутрішніх і зовнішніх загроз життєво важливим інтересам об'єктів економічної безпеки;

• розробка комплексу оперативних і довготривалих заходів щодо попередження і нейтралізації внутрішніх і зовнішніх загроз, оцінка результатів їх здійснення;

• організація роботи із реалізації комплексу державних заходів щодо забезпечення економічної безпеки.

Економічна безпека досягається здійсненням єдиної державної політики, узгодженої, збалансованої, скоординованої системою заходів, адекватних внутрішнім та зовнішнім загрозам. Без вироблення єдиної державної політики забезпечення економічної безпеки неможливо домогтися виходу з кризи, стабілізувати економічну ситуацію в Україні, створити ефективні механізми соціального захисту населення.

Геометрія – частина математики, яка вивчає просторові форми і відносини тіл. На відміну від інших природничих наук, вона вивчає об'єкти реального світу в найбільш абстрактному вигляді, приймаючи до уваги тільки форму та розміри предметів і не враховуючи їх фізичних та інших властивостей (матеріал, міцність, масу, колір, шорсткість поверхонь та інше).

Предмети, що розрізняються за цими властивостями, прийнято називати геометричними фігурами. До них відносяться: точка, пряма, площина, коло, трикутник, круг, куля, куб, паралелепіпед, конус, циліндр та інші. Геометричну фігуру вважають такою, що складається з точок і визначають як будь-яка безліч точок. Безліч усіх точок, що розглядаються в геометрії, називають математичним простором. Будь-яка геометрична фігура є підмножиною простору. Якщо говорять: дана геометрична фігура, то це означає, що виділена вся безліч точок, яка належить даній фігурі.

Основними невизначуваними поняттями геометрії є точка, пряма, площина і відстань. Вони не можуть бути визначені за допомогою інших, простіших понять. Всі ці поняття виникли з безпосереднього спостереження предметів, що оточували нас. Поняття "множина" також є основним, невизначуваним, але не тільки геометрії, а всієї математики.

Точка є результатом перетину двох прямих, прямої та площини, в загальному випадку – трьох площин (наприклад, вершина тетраедра). Точка не має розмірів. Зображення точки дає слід вістря олівця на папері. Пряма – проста лінія, має одне вимірювання. Уявлення про пряму дає натягнута нитка, найкоротша відстань між двома точками, лінія перетинів двох площин, а зображенням її є слід, який залишає на папері вістря олівця, що рухається вподовж краю лінійки.

Площина – проста поверхня, має два вимірювання. Уявлення про площину дає спокійна поверхня води в озері, полірована поверхня столу. В даний час геометрія має численні розділи. Існують елементарна, аналітична, диференціальна, нарисна, проективна та інша геометрія.

Нарисна геометрія є тим розділом геометрії, який вивчає теоретичні основи методів побудови зображень (проекцій) геометричних фігур на будь-якій поверхні та способи рішення різних позиційних і метричних задач, що відносяться до цих фігур, за допомогою їх зображень. Поверхнею, на якій будуються зображення (проекції) предметів, як правило, вибирається площина. У спеціальних розділах нарисної геометрії розглядається побудова зображень на інших поверхнях, наприклад, сферичній, циліндровій і т.п. Нарисна геометрія базується на аксіомах і теоремах елементарної геометрії та інваріантах центрального і паралельного проекціювання.

Сукупність двох і більше взаємозв'язаних зображень предмету називається кресленням. Креслення має виключно велике значення в практичній діяльності людини. Воно є засобом виразу задумів ученого, конструктора та основним виробничим документом, за яким здійснюється будівництво будівель та інженерних споруд, виготовлення машин, механізмів та їх складових частин. Зрозуміло, що не всяке креслення може служити цим цілям, а тільки таке, яке володіє оборотністю, вимірністю, наочністю, геометричною рівноцінністю оригіналу, простотою побудови, точністю графічних рішень.

Креслення є міжнародною графічною мовою, зрозумілою будь-якій технічно грамотній людині. Нарисна геометрія – граматика цієї мови.

Для побудови зображень (проекцій) геометричних фігур нарисна геометрія застосовує метод проекціювання. Креслення, які виходять при цьому, називають проекційними.

Існує два види проекціювання – центральне та паралельне, і відповідно два види проекцій – центральні та паралельні. Побудова проекцій зводиться до побудови проекцій деякої безлічі його точок. Тому вивчення методу проекціювання починають з побудови проекцій точки.

Знання та навики, набуті при вивченні інженерної графіки, послужать надалі основою для вирішення технічних завдань в інженерній практиці. Вивчення інженерної графіки розвиває просторове і логічне мислення, необхідне в будь-якій області інженерної діяльності, та особливо для конструктора і проектувальника.

СИМВОЛІКА І ПОЗНАЧЕННЯ

Знаки геометричні

a). Знаки, що позначають геометричні фігури

Ф (фе – прописна буква грецького алфавіту) – геометрична фігура. А, В, С,...або 1,2, 3,...(прописні букви латинського алфавіту або арабські цифри) – точки простору.

а, b, с,...(рядкові букви латинського алфавіту) – прямі або криві лінії простору.

(АВ) – пряма, що проходить через точки А та В.

[АВ) – промінь з початком у точці А.

[АВ] – відрізок прямої, обмежений точками А та В.

/АВ/ – довжина відрізка [АВ], відстань від точки А до точки В.

/А,а/ – відстань від точки А до прямої а.

/А,Г/ – відстань від точки А до площини Г.

Г (гамма), Δ (дельта), Λ (ламбда), Σ (сігма), Ψ (псі) та інші – (прописні букви грецького алфавіту) – поверхні.

<ABC або α, β, γ,... рядкові букви грецького алфавіту – кути.

П' – площина проекцій, картинна площина.

П₁ – горизонтальна площина проекцій,

П₂ – фронтальна площина проекцій,

П₃ – профільна площина проекцій,

П₄, П₅,... – інші площини проекцій.

А₁, А₂, А₃ – проекції точки А (горизонтальна, фронтальна, профільна).

I₁, І₂, І₃ – проекції лінії І (горизонтальна, фронтальна, профільна).

Г₁(А₁,В₁,С₁,), Г₂(А₂,В₂,С₂), Г₃(А₃,В₃,С₃) – проекції площини Г(АВС), що проходить через точки А, В і С (горизонтальна, фронтальна, профільна).

А_∞ – нескінченно віддалена точка,

a_∞ – нескінченно віддалена пряма,

Г_∞ – нескінченно віддалена площина.

б). Знаки, що позначають відносини між геометричними фігурами

// – паралельність двох геометричних фігур,

^ – перпендикулярність,

_ – прямі, що схрещуються,

⊓ – перетин геометричних фігур (множин),

= – рівні, співпадають або результат перетину геометричних фігур,

– конгруентність.

в). Знаки, що позначають геометричні перетворення

 – відображається.

г). Знаки, що позначають множини, операції над ними і відношення між множинами

А, В, С,... – множини.

Ф – порожня множина.

а, b, с,... – елементи множини.

{...} – складається з, наприклад: М={а, b, с} – безліч М, що складається з елементів а, b, с (і лише з них). М={а:Р(а)} – множина, що складається з таких а, які володіють властивістю Р, наприклад: М={N:(/0N/=R)} – М є безліч таких точок N, відстань яких до точки О рівна R (коло на площині або сфера у просторі).

Î – приналежність, наприклад:

а ) А Î l – точка А належить прямій 1,

б ) b ' М – пряма b проходить через точку М або пряма b містить точку М,

в ) Ï –не належить.

þ – включення (є частиною, підмножиною, міститься в., включає, містить в собі), наприклад:

а ) а þ Г – пряма а належить площині Г (розуміється в сенсі: безліч точок прямої а є підмножина безлічі всіх точок площини Г),

б ) Г ב а –площина Г проходить через пряму а або площина Г містить пряму а.

⊔ – об'єднання множин, наприклад:

АВСD = [АВ] ⊔[ВС] ⊔[СD] – ламана лінія є об'єднання відрізків.

⊓ – перетин множин, наприклад: b = Δ⊓Г – пряма b є перетин Δ і Г.

І ⊓ m = Ф – перетином прямих є порожня множина, тобто прямі паралельні або схрещуються.

д. Знаки, що позначають логічні операції

^ – відповідає кон’юнкції "І".

n – відповідає диз’юнкції "АБО".

] – логічне проходження, означає "якщо..., то"

ó – в тому і лише в тому випадку, якщо....

ЛЕКЦІЯ № · 1. МЕТОДИ ПРОЕКЦІЮВАННЯ

1.1. Центральне проекціювання.

1.2. Паралельне проекціювання.

1.3. Інваріанти паралельного проекціювання.

1.4. Ортогональне проекціювання.

1.1. Центральне проекціювання. Поняття про проекційний простір

Для того, щоб побудувати проекцію, наприклад, деякої точки А, вибирається довільна площина П', звана площиною проекцій, і точка S, що не належить площині П', звана центром проекцій (рис. 1.1).

Рис. 1.1

Операція проекціювання полягає в тому, що через точки S та А проводиться пряма до перетину з площиною П'.

Пряма SА називається проекціювальною прямою, а точка А' перетину проекціювальної прямої з площиною проекцій П', – центральною проекцією точки А на площині П' (рис. 1.1). Можна побудувати центральні проекції інших точок простору (В,С,D...), за винятком тих, які належать площині П, що проходить через центр проекцій S і паралельна П'. В цьому випадку проекціювальні прямі виявляються паралельними площині П', і точок перетину їх з площиною в звичайному сенсі немає. Цей недолік центрального проекціювання усувається доповненням евклідова простору так званими нескінченно віддаленими або невласними елементами.

Доповнення евклідова простору невласними елементами дозволяє ліквідовувати виключення в основних положеннях елементарної геометрії та стверджувати:

· кожні дві прямі, що належать одній площині, завжди перетинаються (у власній або невласній точках);

· дві будь-які площини простору завжди перетинаються (лінія перетину – власна або невласна пряма);

· пряма і площина завжди перетинаються (у власній або невласній точках), отже, проекцією точки С, що належить площині П та П' буде невласна точка С'.

Описаним методом центрального проекціювання може бути побудована проекція будь-якої точки геометричної фігури, а отже, і проекція самої фігури. Наприклад, центральною проекцією відрізка [ВС] на площині П' є безліч центральних проекцій усіх точок відрізка [ВС] – [В'С'] (рис. 1.2).

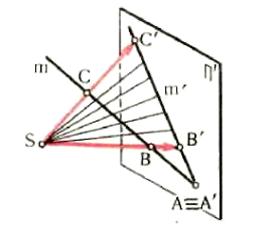
Рис. 1.2

При центральному проекціюванні відбувається спотворення форми, розмірів та деяких інших властивостей предмету (рис. 1.3). Разом з тим, неважко відмітити, що частина властивостей зберігається, наприклад, проекція точки є точка; проекція прямої – теж пряма лінія. Якщо точка належить прямій, то проекція точки належить проекції тієї ж прямої; точка перетину прямих проектується в точку перетину їх проекцій. Проекція предмету, побудована методом центрального проекціювання, називається перспективою (рис. 1.3).

Рис. 1.3

Побудова проекцій паралельно об'єкту називається прямим завданням нарисної геометрії. Неважко відмітити, що метод центрального проекціювання дозволяє вирішувати її однозначно: кожна точка має на площині П' єдину проекцію, оскільки проекціювальна пряма перетинається з площиною П' в одній точці. Так, точка А (рис.1.1) має на площині П' єдину проекцію А', відрізок [ВС] – єдину проекцію [В'С'], будь-яка геометрична фігура – єдину проекцію.

У практичній діяльності необхідно вміти не тільки створювати креслення, але і читати їх, тобто судити за кресленням однозначно про сам предмет. Визначення форми і розмірів об'єкту за його кресленням називається зворотним завданням нарисної геометрії. Одна проекція точки не визначає її положення в просторі, оскільки може бути проекцією будь-якої точки, належної проекціювальній прямій. Так, точка А' (рис. 1.1) може бути проекцією будь-якої точки, що належить прямій SА; [В'С'] на рис. 1.2 – проекцією будь-якої лінії, що належить проекціювальній площині, що визначається точкою S і прямою ВС.

Отже, одна проекція об'єкту не дозволяє судити про його форму і розміри, тобто однопроекційне креслення є необоротним.

1.2. Паралельне проекціювання

Якщо за центр проекцій прийняти невласну точку S простору, то проекціювальні прямі АА₁, В В₁, будуть паралельними між собою. Для їх побудови замість відсутньої на кресленні точки S задають напрям проекціювання s (рис. 1.4).

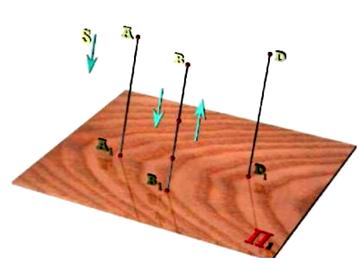
Рис. 1.4

Такий вид проекціювання називається паралельним, а точки А₁, В₁, D₁ перетину проектуючих прямих з площиною проекцій П₁ – паралельними проекціями точок А, В, D, простору. Очевидно, що при паралельному проектуванні, як і при центральному, кожна точка простору має на площині П₁ одну проекцію. Ця проекція не визначає положення точки в просторі.

1.3. Інваріанти паралельного проекціювання

1. Проекція точки на площину є точка (рис. 1.4)

A ·A₁.

2. Проекція прямої в загальному випадку пряма: І  І₁, (рис. 1.5); вона вироджується в точку, якщо пряма паралельна до напряму проекціювання.

Рис. 1.5

3. Якщо точка належить лінії, то проекція точки належить проекції лінії (рис. 1.6).

A Î І A₁ Î І₁

Рис. 1.6

Наслідки з п.п. 2 та 3. Для побудови проекції прямої досить побудувати проекції двох точок, що належать прямій:

A Î І ^ B Î І =A₁ Î І₁ ^ B₁ Î І₁

4. Точка перетину ліній проектується в точку перетину їх проекцій (рис. 1.5):

К = а ⊓ b K₁ = а₁ ⊓ b₁.

5. Проекції паралельних прямих паралельні (рис. 1.6):

І // І' =І₁ // І₁'

Наслідки:

1) відношення довжин відрізків паралельних прямих рівне відношенню довжин їх проекцій (рис. 1.6):

[АВ] // [CD] ]

2) якщо точка, що належить відрізку прямої, ділить його в деякому відношенні, то проекція точки ділить проекцію відрізка в тому ж відношенні (рис. 1.6).

6. Якщо геометрична фігура Ф належить площині Σ, паралельній площині проекцій (наприклад, П₁), то проекція цієї фігури на площину П₁ конгруентна самій фігурі. Наприклад, якщо відрізок МN паралельний площині проекцій, то його проекція на дану площину конгруентна самому відрізку (рис. 1.6).

7. Проекція геометричної фігури не змінюється при паралельному перенесенні площини проекцій.

1.4. Ортогональне проекціювання

Якщо напрям проекціювання перпендикулярний площині проекцій, паралельне проекціювання називається ортогональним (прямокутним):

s ^ П₁  (AA₁) ^ П₁.

В цьому випадку проекція А₁ точки А називається ортогональною, або прямокутною (рис. 1.7). Інакше проекціювання називається косокутним.

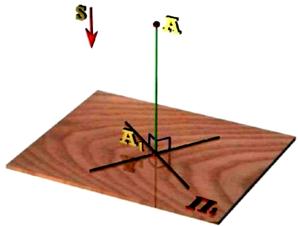
Рис. 1.7

Рис. 1.8

Ортогональне проекціювання, будучи окремим випадком паралельного, значно спрощує побудову проекцій геометричних фігур і є основним при виконанні комплексних креслень технічних форм (рис. 1.8). Розглянуті в попередніх параграфах однопроекційні креслення геометричних фігур є необоротними. За ними не можна в думках відтворити просторову форму і розміри зображеного об'єкту. Існують різні способи усунення цього недоліку однопроекційних креслень залежно від прийнятого виду проекціювання.

Наприклад, при центральному проекціюванні точку можна проектувати з двох різних центрів (рис. 1.9), при паралельному – за допомогою двох різних напрямів, при ортогональному – на дві пересічні площини. Неважко відмітити, що в кожному з цих випадків виходять дві проекції А₁, та А'₁, точки А, що однозначно визначають її положення в просторі.

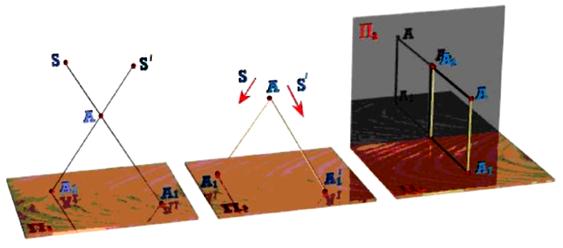
Рис. 1.9

ЛЕКЦІЯ № · 2. КОМПЛЕКСНІ КРЕСЛЕННЯ ГЕОМЕТРИЧНИХ ФІГУР

2.1. Комплексне креслення точки.

2.2. Комплексні креслення ліній.

2.3. Комплексні креслення прямих ліній.

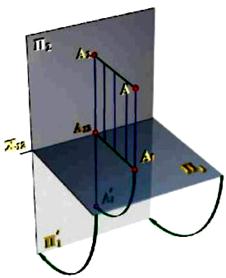
Рис. 2.1

Розглянемо систему двох взаємно перпендикулярних площин П₁ та П₂ (рис. 2.1). Площину П₁ розташуємо горизонтально і назвемо горизонтальною площиною проекцій, а площину П₂, перпендикулярну П₁, розташуємо прямо перед собою і назвемо фронтальною площиною проекцій. Лінія х₁₂ їх перетину називається віссю проекцій.

Візьмемо будь-яку точку А (рис. 2.1) і побудуємо її ортогональні проекції А₁ та А₂ відповідно на площинах П₁ та П₂. Точка А₁ називається горизонтальною проекцією точки А, а точка А₂ – її фронтальною проекцією.Точка А та її ортогональні проекції А₁ та А₂ належать одній площині. [(АА₁) ⊓ (АА₂)], є перпендикулярною П₁, П₂ та осі х₁₂. Відстань |АА₁| точки А до площини П₁ називається висотою точки А, а її відстань |АА₂| до площини П₂ – глибиною точки А.

Просторова модель площин проекцій (рис. 2.1) незручна для практичного використання, оскільки на площині П₁ відбувається спотворення форми і розмірів горизонтальної проекції геометричної фігури. Для того, щоб перейти від просторової моделі площин проекцій до більш простої площинної моделі, тобто до плоского креслення, сумістимо площину П₁ з площиною П₂, обертаючи її навколо осі х₁₂ в напрямі, вказаному на рис. 2.1 стрілками. В результаті отримаємо комплексне креслення точки А, яке складається з комплексу двох її проекцій А₁ та А₂, що належать одній прямій, перпендикулярній осі х₁₂ (рис. 2.1). Пряма (А₁, А₂) та х₁₂, що сполучає дві проекції точки на комплексному кресленні, називається лінією зв'язку. Отримане таким чином комплексне креслення точки буде оборотним, оскільки дві її проекції А₁ та А₂ однозначно визначають положення точки А в просторі.

У технічній практиці для визначення форми та розмірів предмету застосовується принцип внутрішнього координування, при якому задаються розміри предмету, що характеризують форму і взаємне розташування його точок, ліній і поверхонь щодо його конструкторських і технологічних баз, а не щодо площин проекцій. Тому в техніці прийнятий безосний спосіб виконання креслень. Площини проекцій при цьому в просторі не фіксуються, вісь проекцій стає невизначеною і на кресленні не наноситься (рис. 2.2, в). Підставою для цього є те, що проекція геометричної фігури не змінюється при паралельному перенесенні площини проекцій (п.7, розділ 1.3, лекція №·1).

Лінія зв'язку [А₁А₂] на безосному комплексному кресленні проводиться вертикально. Якщо з яких-небудь причин необхідно зафіксувати площини проекцій П₁ та П₂, то на безосному комплексному кресленні наноситься вісь проекцій х₁₂ перпендикулярно лініям зв'язку в будь-якому зручному місці між горизонтальною і фронтальною проекціями геометричної фігури.

У багатьох випадках для виявлення форми і розмірів предмету доводиться будувати його проекції не на дві, а на більшу кількість площин. Значна частина предметів вимагає побудови трьох проекцій. Для побудови третьої проекції предмету застосовується профільна площина проекцій П₃, перпендикулярна П₁ та П₂ (рис. 2.2).

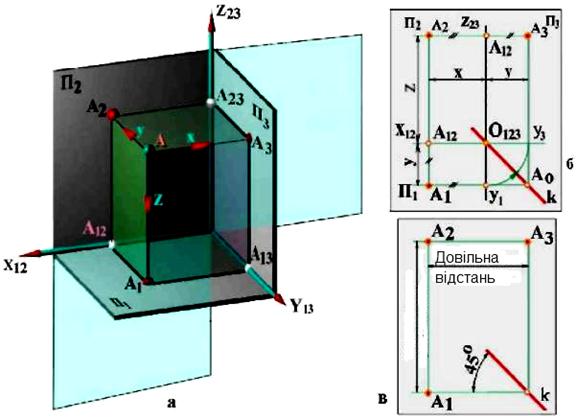
Рис. 2.2

Ортогональна проекція А₃ точки А на профільну площину проекцій називається профільною проекцією точки. Відстань /АА₃/ точки А до площини П₃ називається широтою точки А. Очевидно, що дві будь-які проекції точки А визначають її положення в просторі (рис. 2.2). Утворення комплексного креслення точки А (рис. 2.2, б) зрозуміло з просторового креслення.

За двома заданими проекціями точки можна побудувати її третю проекцію, користуючись умовами зв'язку між проекціями точки на комплексному кресленні (рис. 2.2, б):

· горизонтальна і фронтальна проекції точки належать одній вертикальній лінії зв'язку;

· фронтальна і профільна проекції точки належать одній горизонтальній лінії зв'язку;

· горизонтальна і профільна проекції точки належать ламаній лінії зв'язку, вершина якого належить постійній прямій k креслення (пряма k є бісектрисою прямого кута, утвореного ламаною лінією зв'язку).

На безосному комплексному кресленні умови зв'язку між проекціями точки зберігаються (рис. 2.2, в). Якщо задана система взаємозв'язаних точок А, В, С, то за двома проекціями кожної з точок можна побудувати третю, якщо на ній є три проекції однієї з точок, наприклад точки А (рис. 2.3, а). Точка А називається при цьому базовою.

Рис. 2.3

Якщо прийняти площини проекцій П₁, П₂ та П₃ за координатні площини декартової системи координат, то довжини відрізків, що виражають відстані точки А до площини проекцій, віднесені до одиниці довжини /е/ будуть координатами точки А (рис. 2.2, а, б):

|AA₃| / |e| = x – абсциса (широта);

|A₂| / |e| = у – ордината (глибина);

|A₁| / |e| = z – апліката (висота).

У технічних кресленнях за одиницю довжини приймають |е| = 1·мм. За координатами точки А(х,у,z) можна побудувати її проекції, а за заданими проекціями визначити її координати (рис. 2.2, б). При безосному способі зображення координати точки стають невизначеними. В цьому випадку для побудови комплексного креслення точки можна скористатися різницями координат, які не залежать від положення площин проекцій (рис. 2.3, б), або побудувати на ньому проекції координатних осей і віднести точку до системи координат Охуz (рис. 2.3, в).

Висновки

1.Сукупність двох і більше взаємозв'язаних ортогональних проекцій геометричної фігури, розташованих на одній площині креслення, називається комплексним кресленням.

2.Оборотне комплексне креслення повинне містити не менше двох проекцій геометричної фігури.

3. Для того, щоб креслення геометричної фігури було оборотним, воно повинно містити стільки проекцій, щоб кожна її точка мала не менше двох проекцій.

2.2. Комплексні креслення ліній

Лінії серед геометричних фігур займають особливе положення. Крім службового застосування, при виконанні зображень і різних графічних побудов, вони дають можливість вирішувати багато наукових та інженерних задач. Наприклад, за допомогою ліній можна створити наочні моделі багатьох процесів, встановити і досліджувати функціональну залежність між різними параметрами, конструювати поверхні технічних форм і т.п. Лінію можна представити або як межу поверхні, або як слід безперервно рухомої в просторі точки. Оскільки положення точки на лінії визначається однією безперервно змінною величиною (одним параметром), лінія є однопараметричною (одновимірною) безперервною безліччю точок. Для нарисної геометрії другий, так званий кінематичний, спосіб представлення лінії є зручнішим. Існують прямі, ламані та криві лінії.

2.3. Комплексні креслення прямих ліній

Пряма є така безліч точок, властивості якої визначаються відомою аксіомою прямої лінії: "через будь-які дві різні точки проходить одна і лише одна пряма" і теоремою, яка виходить з аксіоми прямої: "дві різні прямі можуть мати не більше за одну загальну точку".

Дата добавления: 2014-01-07