Перевірка статистичних гіпотез

Під статичною гіпотезою розуміють усяке припущення про генеральну сукупність, що перевіряється за вибіркою. Статистичні гіпотези класифікують на гіпотези про закони розподілу й гіпотези про параметри розподілу. Так, наприклад, гіпотеза про те, що продуктивність праці робітників, які виконують однакову роботу в однакових організаційно-технічних умовах, має нормальний закон розподілу, є гіпотезою про закон розподілу. Гіпотеза про те, що середні розміри деталей, вироблених на однотипних, паралельно працюючих верстатах, не розрізняються між собою, є гіпотезою про параметри розподілу.

Одну із гіпотез виділяють у якості основної й позначають Н₀. Разом з основною завжди розглядається альтернативна (конкуруюча) гіпотеза, що позначається Н₁. Вибір альтернативної гіпотези визначається конкретним формулюванням задачі. На основі статистичних даних дуже важко, а іноді й неможливо зробити безпомилкові висновки. Помилки при перевірці гіпотез бувають 2-х видів:

- помилка 1-го роду полягає в тому, що відхиляється гіпотеза Н₀ у той час як вона вірна;

- помилка 2-го роду полягає в тому, що відхиляється альтернативна гіпотеза в той час як вона вірна;

При перевірці статичних гіпотез на основі статистичних даних важливо знайти такий спосіб, щоб ймовірність помилок була мінімальна. Правило, за якім приймається рішення прийняти або відхилити гіпотезу Н₀, називається критерієм К. Перевірка статичних гіпотез ґрунтується на принципі, відповідно до якого малоймовірна подія вважається неможливою, а подія, що має велику ймовірність – достовірною. Цей принцип реалізується в такий спосіб: фіксується деяка ймовірність (з найпоширенішим рівнем значущості 0,05; 0,01; 0,25; 0,001, потім підбирається деяка статистика z, що формально відбиває зміст гіпотези й розподіл якої відомо. Нехай V – множина значень статистики z. Всю множину значень статистики z можна розбити на дві підмножини, таких, що:

- гіпотеза, що перевіряється, повинна бути відкинута, якщо значення z попадає в одну з підмножин, яка називається критичною областю V. За умови істинності гіпотези Н₀ ймовірність попадання статистики в Vдорівнює a, тобто .

- гіпотеза Н₀ , що перевіряється, повинна бути прийнята, якщо значення z попадає в підмножину V \ V. Ця підмножина називається областю припустимих значень.

Позначимо через вибіркове значення статистики z, що обчислене за вибіркою спостережень. Критерій формулюється наступним способом:

- відхилити гіпотезу Н₀ , якщо ;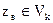

- прийняти гіпотезу Н₀, якщо .

Критерій, заснований на використанні заздалегідь заданого рівня значущості, називають критерієм значущості. Рівень значущості a визначає «розмір» критичної області V.

Основні задачі при перевірці статистичних гіпотез зводяться до відшукання критичної області й області припустимих значень із деякою заданою ймовірністю. Положення критичної області V_k на множині значень статистики z_в залежить від альтернативної гіпотези Н₁.

Нехай f(z/ Н₀) щільність розподілу статистики z критерію за умови, що вірна гіпотеза Н₀. Перевіряється гіпотеза , альтернативна . Положення критичної області показано на Рисунку 23.

Рисунок 23. Положення критичної області у випадку ,

Границя критичної області 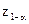- квантиль розподілу статистики f(z/ Н₀).

Тепер нехай альтернативна . Розташування критичної області в цьому випадку показано на Рисунку 24. У розглянутих випадках критерій називається однобічним. При альтернативі критична область показана на Рисунку 25. Критерій у цьому випадку називається двостороннім. 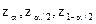- квантилі розподілу статистики f(z/ Н₀).

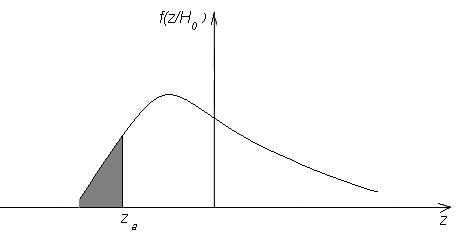
Рисунок 24. Положення критичної області у випадку ,

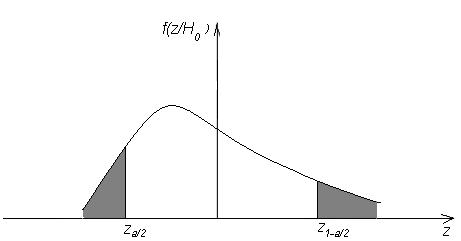
Рисунок 25. Положення критичної області у випадку,.

Таким чином, перевірка статистичної гіпотези за допомогою критерію значущості може бути розбита на наступні етапи:

1) сформулювати гіпотезу Н₀, що перевіряється і альтернативну гіпотезу Н₁;

2) вибрати рівень значущості ;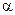

3) вибрати статистику z критерію для перевірки гіпотези Н₀;

4) визначити вибірковий розподіл статистики z за умови, що вірна гіпотеза Н₀;

5) залежно від формулювання альтернативної гіпотези визначити критичну область Vодним з нерівностей або сукупністю нерівностей ;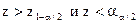

6) отримати вибірку спостережень і обчислити статистики критерію;

7) прийняти статистичне рішення:

якщо 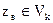, то відхилити гіпотезу Н₀ як таку, що не узгоджується з результатами спостережень;

якщо , то прийняти гіпотезу Н₀ , тобто вважати, що гіпотеза Н₀ не суперечить результатам спостережень.

Зауваження. Звичайно на етапах 4) - 7) використовують статистику, квантили якої табульовані, тобто є таблиці квантилей.

Розглянемо кілька прикладів.

Нехай спостерігаються випадкові величини, кожна з яких підкоряється нормальному розподілу

Нехай є дві незалежні вибірки обсягами nі n:

і

Перевіримо гіпотезу, яка полягає в тім, що математичні сподівання обох випадкових величин однакові в припущенні, що - невідомі й рівні.

Отже,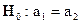

Альтернативною може бути одна з гіпотез:

Розглянемо статистику

, (64)

де 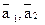- оцінки математичного сподівання, обчислені за формулою (52),

- оцінки дисперсії, обчислені за формулою (53). Ця статистика має розподіл Стьюдента з 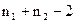порядками волі. Задамо рівень значущості 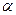й за вибірковим даними обчислимо значення статистику за формулою (17). Визначимо область прийняття гіпотези Н₀:

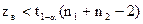при альтернативній ;

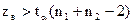при альтернативній ;

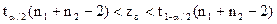при альтернативній . По властивості квантилей розподілу Стьюдента , тоді нерівність прийме вид

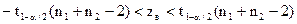, тобто

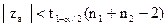
Приклад 25.

При вимірі продуктивності двох агрегатів отримані наступні результати (Таблиця 9), у кг. речовини за годину роботи:

Таблиця 9. Продуктивності двох агрегатів

Агрегат А (x)	14,1 10,1 14,7 13,7 14,0
Агрегат В (y)	14,0 14,5 13,7 12,7 14,1

Чи можна вважати, що продуктивність обох агрегатів однакова в припущенні, що обидві вибірки отримані з нормальних сукупностей з однаковою дисперсією?

У цьому випадку . Сформулюємо основну й альтернативну гіпотези, виходячи з умови задачі:

Обчислимо необхідні величини за формулами:

, , , .

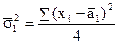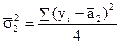
Допоміжні розрахунки представимо в Таблиці 10.

Таблиця 10 Допоміжні розрахунки

x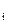
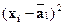
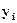
14,1	0,78	0,61	14,0	0,2	0,04
10,1	-3,22	10,37	14,5	0,7	0,49
14,7	1,38	1,90	13,7	-0,1	0,01
13,7	0,38	0,14	12,7	-1,1	1,21
14,0	0,68	0,46	14,1	0,3	0,09
66,6	-	13,48	69,0	-	1,84

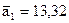
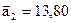
Підставляючи знайдені значення у формулу (64), одержимо

Задамо й за таблицею квантилей розподілу Стьюдента знаходимо:

,

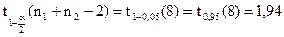0,55< 1,94

Звідси випливає, що гіпотеза приймається, тобто середня продуктивність обох агрегатів однакова.

Перевіримо гіпотезу, що полягає в тому, що дисперсії обох випадкових величин однакові в припущенні, що - невідомі.

, альтернативної може бути одна з гіпотез:

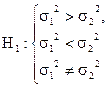
Розглянемо статистику

z = 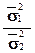(65)

- точкові оцінки, отримані за формулою (53).

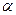Зазначимо, що завжди можна так ввести позначення, що виявиться , таким чином, z повинне бути не менше одиниці. Статистика (65) має розподіл Фішера зі порядками волі. Задамо рівень значущості й за вибірковим даними обчислимо значення статистику за формулою (18). Визначимо область прийняття гіпотези Н₀:

при альтернативній ;

при альтернативній ;

при альтернативній 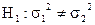. За властивістю квантилей розподілу Фішера 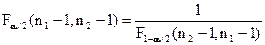, тоді нерівність набуває вигляду , що еквівалентно нерівності .

Гіпотеза про рівність дисперсій звичайно застосовується тоді, коли потрібно зрівняти точність або ризики.

Приклад 26. Біржовий маклер досліджує дві інвестиції – А и В від імені клієнта. Інвестиція А передбачається на строк 10 років з очікуваним середнім щорічним прибутком 17,8% і середньоквадратичним відхиленням 3,21%. Інвестиція В розрахована на строк 8 років також з очікуваним прибутком 17,8% і середньоквадратичним відхиленням 7,14%. Чи можна вважати, що ризик інвестиції В більше, ніж інвестиції А? Передбачається, що розподіл щорічних прибутків на інвестиції підкоряється нормальному розподілу.

Дисперсія щорічних прибутків може бути використана для визначення ризику. Тому задачі зводиться до перевірки гіпотези про рівність дисперсій за альтернативи , тобто

Обчислимо оцінки дисперсій за формулою (10)

Приймемо рівень значущості 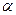= 0,05.

Вибіркова статистика z= . За таблицею Додатка 5 знайдемо квантиль розподілу Фішера

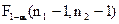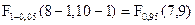= = 3,29

5,09= z > =3,29.

Статистика z попадає в критичну область, отже, гіпотеза Н₀ відхиляється, тобто є підстави вважати, що ризик інвестиції В більше, ніж ризик інвестиції А.

Дата добавления: 2014-01-07