Уточнення коренів рівняння методом хорд

Доведення

За теоремою Лагранжа.

#

(МЕТОД ПРОПОРЦІЙНИХ ВІДРІЗКІВ)

Нехай дано рівняння 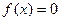. Залишемо в силі припущення попереднього параграфа. Розглянемо геометрично.

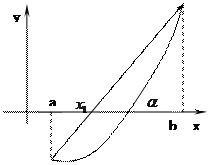
Мал.1 Мал.2

Виведемо рекурентну формулу для побудови наближення:

...

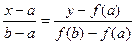
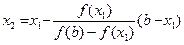
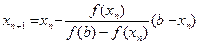(2)

Доведемо збіжність даного процесу: послідовність 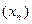монотонно зростає і обмежена зверху, тому 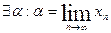, в рівнянні (2) перейдемо до границі: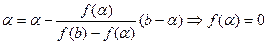

Зауваження: в загальному випадку за нерухому точку вибирають той кінець відрізка [a,b] в якому знак функції f співпадає з знаком другої похідної, тоді (2) буде:

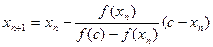, (3)

Другий кінець проміжка зручно вибирати за початкове наближення.

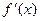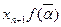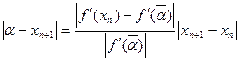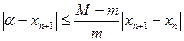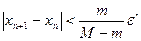Виведемо формулу для оцінки точності. Нехай похідна неперервна на [a,b], тоді вона приймає найбільше і найменше значення, тобто , . Застосуємо теорему Лагранжа:. Розкривши душки додавши до обох частин рівності вираз і звівши подібні доданки, отримаємо:. Врахувавши межі зміни похідної (4) (5).

Виникає питання про можливість використання оцінки (5), коли мінімум похідної =0.

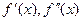Теорема: нехай на відрізку [a,b] функція f(x) неперервна разом зі своїми похідними до 2-го порядку включно, причому . Нехай також похідні зберігають на [a,b] сталі знаки, тобі існує такий окіл кореня , що для 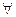початкового наближення 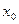з цього околу послідовність (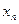), яка обчислюється за формулою (3), збігається до .

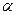Доведення

Щоб скористатися принципом стискуючого відображення досить показати, що в деякому околі R кореня 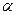похідна функції , задовільняє умову .

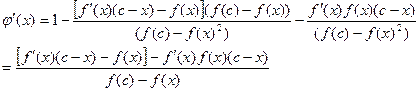
Підставимо :. Запишемо для f(x) формулу Тейлора і обмежимося 3-ма доданками, тобі: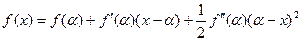. Підставивши в останню рівність x=c, отримаємо: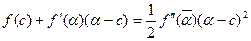 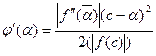, оскільки при : то можна виділити такий окіл R:

§5 МЕТОД ДОТИЧНИХ (МЕТОД НЬЮТОНА)

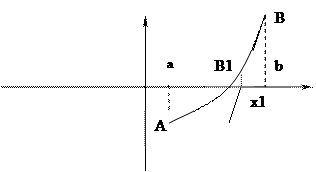
Розглянемо геометричну інтерпритацію даного методу. Нехай маємо рівняння 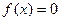(1) і всі умови попереднього § виконуються. Беремо точку B, проводимо в ній дотичну.

Рівняння дотичної в точці 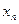має вигляд , знайдемо точку :

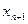(2)

Зауваження: в якості вихідної точки 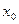слід вибирати той кінець відрізка [a,b] в якому функція має той самий знак, що і її друга похідна.

У випадку зображеному на малюнку послідовність 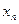монотонно спадає і обмежена знизу, а отже вона збіжна, тобто 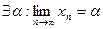. Перейшовши до границі в рівності (2) отримаємо: В загальному випадку справедлива така теорема.

Теорема: нехай на відрізок [a,b] функція f(x) неперервна разом з своїми похідними другого порядку включно. Тоді існує деякий окіл 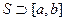, що 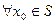послідовність 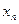обчислена за формулою (2) збігається до кореня рівняння.

Дата добавления: 2014-01-07