Обернена матриця

Означення. Оберненою до даної квадратної матриці 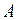називається така матриця , добуток на яку матриці 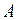справа є одиничною матрицею: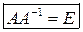

Теорема. Для кожної неособливої квадратної матриці існує обернена, притому тільки одна. Для особливої квадратної матриці обернена не існує.

Робоча формула для обчислення матриці , оберненої для матриці 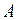, має вигляд:

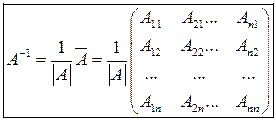
2.4. Означення рангу матриці.

Розглянемо прямокутну матрицю А, яка складається з т рядків та п стовпців:

.

Нехай 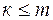і . Виділимо в цій матриці 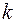рядків і 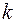стовпців. Із елементів, що стоять на перетині виділених рядків і стовпців, складtмо визначник 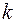-го порядку. Будь-який подібний визначник називається мінором матриці А.

Означення. Рангом матриці А називається найвищий порядок відмінного від нуля мінора цієї матриці.

Якщо ранг матриці 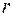, то серед мінорів цієї матриці є принаймні один мінор 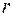-го порядку, відмінний від нуля. В той же час всі мінори -го і вищих порядків дорівнюють нулеві. Позначають ранг матриці через 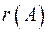. Для обчислення рангу матриці її спочатку спрощують за допомогою елементарних перетворень.

2.5. Елементарні перетворення матриць.

До елементарних перетворень матриці відносять: транспонування; перестановку двох рядків (стовпців); множення всіх елементів рядка (стовпця) на довільне число 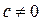; додавання до всіх елементів рядка (стовпця) відповідних елементів паралельного рядка (стовпця), помножених на одне і те ж число.

Теорема 1. (про елементарні перетворення). При елементарних перетвореннях матриці її ранг не змінюється.

2.6. Обчислення рангу матриці.

За допомогою елементарних перетворень будь-яку матрицю можна звести до матриці виду:

,

де на головній діагоналі стоять 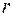одиниць а всі інші елементи дорівнюють нулю. Ранг одержаної, а отже, і даної матриць дорівнює .

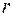Приклад. За допомогою елементарних перетворень обчислити ранг матриці:

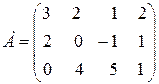
Розв’язання. Віднімаючи від ІІІ рядка подвоєний І і додаючи потроєний ІІ, одержимо:

Віднімаючи ІV стовпчик від I, II від IV, маємо:

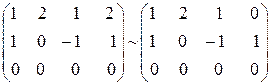
Віднімаючи ІV стовпчик від I, скорочуючи II на 2 і віднімаючи від III, маємо:

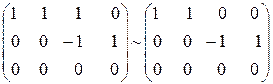
Віднявши I від II, додавши ІV до III і помінявши місцями II і ІV стовпчик, маємо:

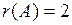
2.7. Поняття лінійної залежності.

Важливе значення в лінійній та векторній алгебрі має поняття лінійної залежності елементів. Позначимо рядки матриці А через l₁ , l₂ , …, l_m.

Означення. Рядки матриці називаються лінійно залежними, якщо можна підібрати числа , не рівні одночасно нулеві, такі, що: . Якщо таких чисел не існує, тобто дана рівність виконується лише при умові , то рядки називають лінійно незалежними.

Коли один рядок матриці лінійно виражається через інші, то система рядків лінійно залежна, наприклад:

.

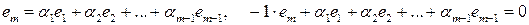І навпаки, якщо система рядків лінійно залежна, то принаймні один рядок лінійно виражається через інші; наприклад, .

2.8. Теорема про ранг матриці.

Теорема 2 (про ранг матриці). Якщо ранг матриці r, то в цій матриці можна знайти r лінійно незалежних рядків (стовпців), через які лінійно виражаються всі інші її рядки (стовпці).

Наслідок 1. Максимальне число лінійно незалежних стовпців матриці дорівнює максимальному числу лінійно незалежних рядків, бо при транспонуванні матриці ранг не змінюється.

Наслідок 2. Для того, щоб визначник дорівнював нулю, необхідно і достатньо, щоб його рядки (стовпці) були лінійно залежними.

Якщо , то – рядки лінійно залежні. Якщо рядки лінійно залежні, то ранг менше 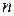i .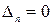

3. Поняття про СЛАР та її розв’язки.

3.1. Поняття про систему рівнянь та її розв’язки.

Розглянемо систему m лінійних рівнянь з n невідомими:

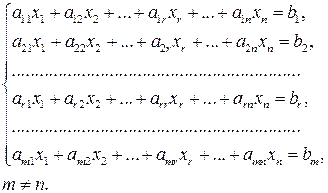
Розв’язком даної системи називається сукупність 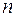значень невідомих , при підстановці яких в систему кожне рівняння перетворюється на тотожність. Система, що має принаймні один розв’язок, називається сумісною; система, що не має жодного розв’язку, – несумісною. Сумісна система, що має єдиний розв’язок, називається визначеною; система, що має більше одного розв’язку, – невизначеною.

Розглянемо основну матрицю системи, складену з коефіцієнтів при невідомих, і матрицю 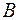, одержану з матриці приєднанням стовпця вільних членів і названу розширеною.

Очевидно, що 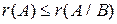, т. я. кожний мінор матриці 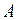є мінором матриці .

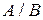3.2. Сумісність СЛАР. Теорема Кронекера-Капеллі.

Теорема Кронекера-Капеллі. Для сумісності системи необхідно і достатньо, щоб ранг розширеної матриці 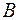системи дорівнював рангу основної матриці .

Отже, якщо 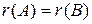, то система сумісна (визначена, невизначена), якщо – система несумісна.

Еквівалентні перетворення системи.

Розглянемо систему:

Теорема. Якщо обидві частини деякого рівняння системи 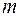лінійних рівнянь з 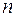невідомими помножити на довільне число 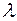і відняти від відповідних частин другого рівняння, то одержимо нову систему, еквівалентну початковій, тобто вони або обидві несумісні, або обидві сумісні і мають одні і ті ж розв’язки.

Наслідок. Якщо скінченне число разів від довільних рівнянь системи відняти будь-які інші рівняння, помножені на сталі, то одержимо систему, еквівалентну даній.

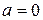При виконанні вказаного перетворення одно або декілька рівнянь можуть набути вигляду: . Якщо , то рівняння лінійно залежні. Якщо 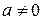, то рівняння і система не мають розв’язку.

4. Методи розв’язання СЛАР

4.1. Правило Крамера розв’язуванння системи n рівнянь з n невідомими.

Застосуємо визначники та їх властивості до розв’язування системи трьох лінійних рівнянь з трьома невідомими.

Нехай дано систему трьох лінійних рівнянь з трьома невідомими:

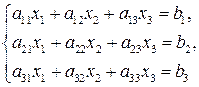
де - коефіцієнти системи, - вільні члени. Якщо , система називається однорідною, якщо хоч один вільний член відмінний від нуля, – неоднорідною. Розв’язком системи називається будь-яка трійка чисел , що перетворює рівняння системи в тотожності.

Розглянемо визначник 3-го порядку, складений з коефіцієнтів при невідомих, назвемо його основним визначником системи:

Введемо також наступні позначення:

,

Припустивши, що, одержимо єдиний розв’язок системи:

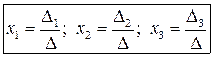
Підставляючи знайдені значення в рівняння системи, переконуємося, що кожне з рівнянь перетворюється в тотожність. Пропонується зробити це самостійно.

Теорема (правило) Крамера. Якщо визначник системи не дорівнює нулю, то система має єдиний розв’язок, який розв’язок знаходимо за формулами:

,

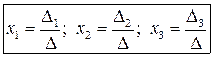де 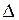- головний визначник системи, а – визначники, одержані з нього заміною відповідно І, ІІ, ІІІ, стовпця вільними членами.

Приклад. Розв’язати систему рівнянь:

Розв’язання.

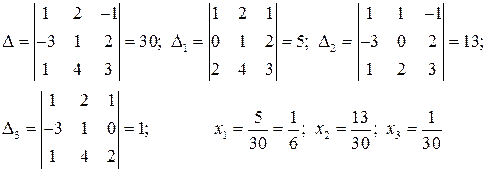
Нехай головний визначник системи дорівнює нулю. Якщо при цьому хоч один з визначників не дорівнює нулеві, то система несумісна.

Дійсно, якщо , то 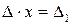не виконується при кожному значенні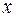. Якщо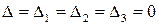, то система або не має розв’язку, або має незчислену множину розв’язків.

Ми записали формули Крамера для розв’язування системи трьох рівнянь з трьома невідомими, ці формули справедливі і для n рівнянь з n невідомими, якщо :

.

4.2. Матричний метод розв‘язування систем n лінійних рівнянь з n невідомими.

Розглянемо систему n лінійних рівнянь з n невідомими:

Виведемо наступні позначення

;

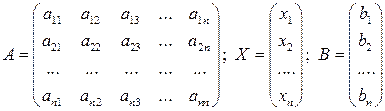Отже, – матриця коефіцієнтів при невідомих, 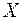– матриця-стовпчик із невідомих, 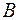– матриця-стовпчик вільних членів.

Тоді систему 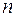лінійних рівнянь з 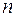невідомими можна записати у матричній формі 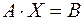або:

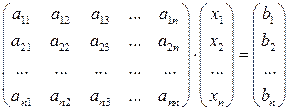
Дійсно, виконавши множення в лівій частині, одержимо

Пригадавши означення рівності двох матриць одержимо дану систему 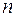рівнянь з 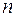невідомими.

Розв’язування матричних рівнянь.

Рівність 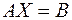являє собою матричне рівняння, в якому невідома матриця – стовпчик 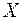. Це рівняння можна розв’язати, якщо матриця – неособлива (тобто визначник системи не дорівнює нулю). В цьому випадку для матриці існує обернена матриця . Помноживши обидві частини матричного рівняння на зліва одержимо:

Останнюрівність називають розв’язком системи в матричній формі. Невідома матриця 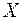виражена через відомі матриц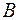і і .

Приклад. Розв’язати систему:

Розв’язання.

;

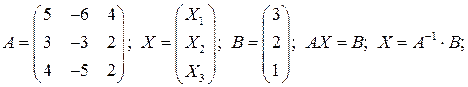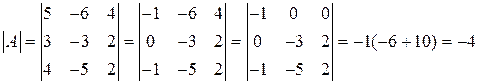
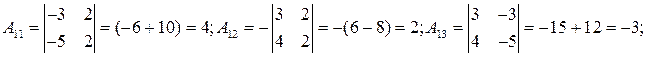
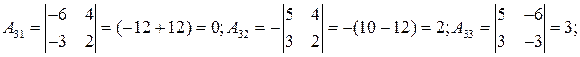
тоді маємо обернену матрицю та шуканий розв’язок:

;

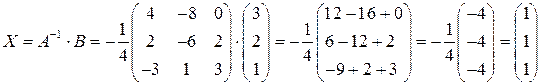
Відповідь:

Дата добавления: 2014-01-07