Корреляционная функция случайной функции

Рассмотрим случайную функцию X(t). При двух фиксированных значениях аргумента, например при t = t₁ и t = t₂ получим два сечения - систему двух случайных величин X(t₁) и Х(t₂) с корреляционным моментом , где

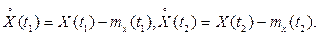
Таким образом, каждая пара чисел t₁ и t₂ определяет систему двух случайных величин, а каждой такой системе соответствует ее корреляционный момент. Отсюда следует, что каждой паре фиксированных значений t₁ и t₂, соответствует определенный корреляционный момент; это означает, что корреляционный момент случайной функции есть функция (неслучайная) двух независимых аргументов t₁ и t₂; ее обозначают через K_x(t₁, t₂). В частном случае значения обоих аргументов могут быть равны между собой.

Приведем теперь определение корреляционной функции.

Определение 2.6. Корреляционной функцией случайной функции X(t) называют неслучайную функцию K_x(t₁, t₂) двух независимых аргументов t₁ и t₂, значение которой при каждой паре фиксированных значений аргументов равно корреляционному моменту сечений, соответствующих этим же фиксированным значениям аргументов:

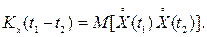
Замечание. При равных между собой значениях аргументов t₁ = t₂= t корреляционная функция случайной функции равна дисперсии этой функции:

K_x(t₁, t₂) = D_x(t).

Таким образом, достаточно знать корреляционную функцию, чтобы найти дисперсию случайной функции.

Свойства корреляционной функции

Свойство 1. При перестановке аргументов корреляционная функция не изменяется (свойство симметрии.):

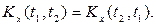
Прибавление к случайной функции X(t) неслучайного слагаемого не изменяет ее центрированной функции.

Свойство 2. Прибавление к случайной функции X(t) неслучайного слагаемого j(t) не изменяет ее корреляционной функции:

если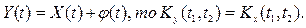

Замечание 1. При умножении случайной функции X(t) на неслучайный множитель j(t) ее центрированная функция умножается на этот множитель.

Свойство 3. При умножении случайной функции X(t) на неслучайный множитель j(t) ее корреляционная функция умножается на произведение j(t₁) j(t₂):

если

Свойство 4. Абсолютная величина корреляционной функции не превышает среднего геометрического дисперсий соответствующих сечений:

.

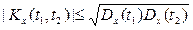Определение 2.7. Нормированной корреляционной функцией случайной функции X(t), называют неслучайную функцию двух независимых переменных t₁ и t₂, значения которой при каждой паре фиксированных значений аргументов равно коэффициенту корреляции сечений, соответствующих этим же фиксированным значениям аргументов:

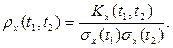(1)

Учитывая, что и 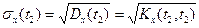, получим

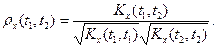(2)

Нормированная корреляционная функция имеет те же свойства, что и корреляционная функция, причем абсолютная величина нормированной корреляционной функции не превышает единицы

Вероятностный смысл нормированной корреляционной функции заключается в том, что чем ближе модуль этой функции к 1, тем линейная связь между сечениями сильнее, и наоборот, чем ближе модуль этой функции к 0, тем линейная связь между сечениями слабее.

Определение 2.8. Взаимной корреляционной функцией двух случайных функций X(t) и Y(t) называют неслучайную функцию R_xy(t₁, t₂) двух независимых аргументов t₁ и t₂, значение которой при каждой паре фиксированных значений аргументов равно корреляционному моменту сечений обеих функций, соответствующих этим же фиксированным значе­ниям аргументов:

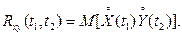
Коррелированными называют две случайные функции, если их взаимная корреляционная функция не равна тождественно нулю.

Некоррелированными называют две случайные функции, если их взаимная корреляционная функция тождественно равна нулю.

Свойства взаимной корреляционной функции

Свойство 1. При одновременной перестановке индексов и аргументов взаимная корреляционная функция не изменяется:

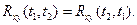
Свойство 2. Прибавление к случайным функциям X(t) и Y(t) неслучайных слагаемых, соответственно j(t) и y(t), не изменяет их взаимную корреляционную функцию:

если и то

Свойство 3. При умножении случайных функций X(t) и Y(t) на неслучайные множители, соответственно j(t) и y(t), взаимная корреляционная функция умножается на произведение j(t₁)y(t₂):

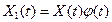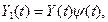если и то

Свойство 4. Абсолютная величина взаимной корреляционной функции двух случайных функций не превышает среднего геометрического их дис­персий:

Определение 2.9. Нормированной взаимной корреляционной функцией двух случайных функций X(t) и Y(t) называют неслучайную функцию двух независимых аргументов t₁ и t₂:

.

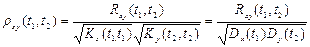Теорема 2.1. Корреляционная функция суммы двух коррелированных случайных функций равна сумме корреляционных функций слагаемых и взаимной корреляционной функции, которая прибавляется дважды (с разным порядком следования аргументов):

если Z(t)=X(t) + Y(t),

то K_z(t₁,t₂)= K_x (t₁,t₂) + K_y(t₁,t₂)+ R_xy (t₁,t₂)+ R_xy (t₂,t₁)

Следствие 1. Корреляционная функция суммы двух некоррелированных случайных функций равна сумме корреляционных функций слагаемых:

если Z(t)=X(t) + Y(t), то K_z(t₁,t₂)= K_x (t₁,t₂) + K_y (t₁,t₂).

Следствие 2. Корреляционная функция случайной функции X(t) и некоррелированной с ней случайной величины Y равна сумме корреляционных функций случайной функции и дисперсии случайной величины:

если Z(t)=X(t) + Y, то K_z(t₁,t₂)= K_x (t₁,t₂) +D_y.

Заключение

Задание студентам для самостоятельной учебной работы, список рекомендуемой литературы и методические указания.

1. Доказать самостоятельно свойства математического ожидания и дисперсии случайной функции, свойства корреляционной функции.

2. Использованная для подготовки лекции литература:

1) Гмурман В.Е. Теория вероятностей и математическая статистика. Учеб. пособие для вузов. - Изд. 11-е, стер. - М.: Высш.шк., 2005. - 479с: ил.

2) Вентцель Е.С., Овчаров Л.А. Теория случайных процессов и ее инженерные приложения. - Учеб. Пособие для втузов. - 2-е изд., стер. - М.: Высш.шк., 2000. - 383с: ил.

3) Волков И.К., Зуев С.М., Цветкова Г.М. Случайные процессы: Учебник для вузов / Под редакцией В.С. Зарубина, А.П. Крищенко. – 2-е изд., стереотип. – М.: Изд-во МГТУ им. Баумана, 2003. – 448 с.

Лекция разработана

доцентом кафедры КБ

к.ф.-м.н, Зайцевой И.В.

_______________________

«____»___________200__г.

Дата добавления: 2014-01-07