
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Несимметричные двойственные задачи
|
|
|
|
Запишем задачу линейного программирования на max в каноническом виде.
Max Z = 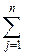 c j x j
c j x j
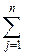 a ij x j = b i
a ij x j = b i
Для записи двойственной задачи представим ограничения равенства в виде системы равносильных неравенств.
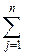 a ij x j <= b I
a ij x j <= b I 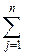 a ij x j => b I,умножим на(-
a ij x j => b I,умножим на(-
1)получим задачу в симметричной форме. Max Z =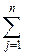 c j x j
c j x j
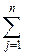 a ij x j <= b I
a ij x j <= b I
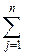 (-a ij) x j <= -b I
(-a ij) x j <= -b I
Введем двойственные переменные Y’i, Y” i, тогда двойственная задача примет следующий вид:
Min f = 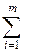 bi (Y’i -Y” i)
bi (Y’i -Y” i)
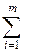 a ij (Y’i -Y” i)=> c j
a ij (Y’i -Y” i)=> c j
Y’I =>0
Y” i =>0
Введем (Y’i -Y” i)= Y i
Min f = ∑bi Y i
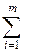 a ij Y i => c j
a ij Y i => c j
Y’I и Y” i, были введены для каждой системы ограничений. Получается, что Y i может принимать как положительные, так и отрицательные значения. Таким образом эта модель представляет собой пару несимметричных двойственных задач. Так же формируется двойственная задача в случае, когда в ограничении исходной задачи входят как неравенства, так и равенства.
Max Z=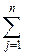 c j x j c j x j
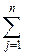 a ij x j <= b I (i=1,…,m) a ij x j <= b I (i=1,…,m)
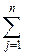 a ij x j =b i (i = M1+1…,m)
x j =>0 (j=1,..n1)
x j (J=n1+1) a ij x j =b i (i = M1+1…,m)
x j =>0 (j=1,..n1)
x j (J=n1+1)
| Min f=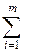 b i x i b i x i
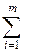 a ij Y i => c j a ij Y i => c j
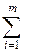 a ij Y i = c j (j= n1+1,…,n)
Y i=>0 (i=1,….,1m 1) a ij Y i = c j (j= n1+1,…,n)
Y i=>0 (i=1,….,1m 1)
|
При этом выполняется ряд правил:
1.Если на переменную xj прямой задачи накладывается условие неотрицательности, то j – условие системы ограничений двойственной задачи записывается в виде неравенств и наоборот.
2.Если на переменную xj прямой задачи не наложено условие неотрицательности, то j – ограничение двойственной задачи запишется в виде строгого равенства.
3.Если в прямой задаче имеются ограничения равенства, то на соответствующие переменные двойственной задачи не налагаются условия неотрицательности.
ТЕОРЕМЫ:
1.Для любых допустимых планов x = (x1,…,x n) и y = (y1,…y m) прямой и двойственной задач линейного программирования справедливо неравенство:
|
|
|
Z (x)<= f (x)
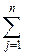 c j x j <=
c j x j <= 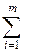 b i y i
b i y i
2.Критерий оптимальности Канторовича. Если для некоторых дополнительных планов x* и y* пары двойственных задач выполняется равенство Z (x*)= f (y*), то x* и y* являются оптимальными планами соответствующих задач.
3. Малая теорема двойственности. Для существования оптимального плана любой из пары двойственных задач необходимо и достаточно существование допустимого плана для каждой из них.
4.Если одна из двойственных задач имеет оптимальное решение, то и другая имеет оптимальное решение. Причем экстремальные значения целевых функций должны быть равны. Если одна из двойственных задач не разрешима вследствие неограниченности целевой функции на множестве допустимых решений, то система ограничений другой задачи противоречива.
5. Теорема о допускающей нежесткости. Для того, чтобы планы x* и y* пары двойственной задачи были оптимальны, необходимо и достаточно выполнение условий:
X*j (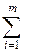 a ij y j * - c j) =0 j= 1,…., n
a ij y j * - c j) =0 j= 1,…., n
Y i* (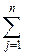 a ij x*j - b i) =0 i= 1,…., m
a ij x*j - b i) =0 i= 1,…., m
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 464; Нарушение авторских прав?; Мы поможем в написании вашей работы!