
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Типы линейных дифференциальных уравнений в частных производных второго порядка
|
|
|
|
Рассмотрим линейное д.у. в ч.п. второго порядка от 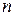 независимых переменных
независимых переменных
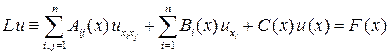
где 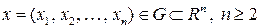 . Коэффициенты
. Коэффициенты 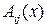 ,
, 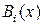 ,
, 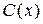 и
и  – заданные в области
– заданные в области  достаточно гладкие функции. В точках
достаточно гладкие функции. В точках  , где все коэффициенты
, где все коэффициенты 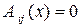 , где
, где  , уравнение (1) вырождается в уравнение первого порядка. Далее будем предполагать, что всюду в области
, уравнение (1) вырождается в уравнение первого порядка. Далее будем предполагать, что всюду в области  порядок уравнения равен двум, то есть коэффициенты
порядок уравнения равен двум, то есть коэффициенты  одновременно в области
одновременно в области  в нуль не обращаются, причем
в нуль не обращаются, причем  .
.
Пусть  – произвольная, но фиксированная точка области
– произвольная, но фиксированная точка области  . Составим квадратичную форму от переменных
. Составим квадратичную форму от переменных  , соответствующую уравнению (1):
, соответствующую уравнению (1):
 . (2)
. (2)
Как известно из курса алгебры квадратичная форма (2) при помощи неособого линейного преобразования переменных 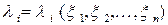 ,
, 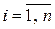 приводится к каноническому виду:
приводится к каноническому виду:
 ,
, 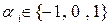 . (3)
. (3)
Причем, согласно закону инерции, число положительных, отрицательных и равных нулю коэффициентов формы (3) являются инвариантами неособенных линейных преобразований.
Определение 1. Когда все 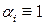 или
или 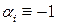 ,
, 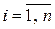 , т.е. когда форма (2) соответственно положительно или отрицательно определена, то д.у. (1) называют эллиптическим в точке
, т.е. когда форма (2) соответственно положительно или отрицательно определена, то д.у. (1) называют эллиптическим в точке 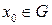 .
.
Если один из коэффициентов  отрицателен, а все остальные положительны (или наоборот), то д.у. (1) называют гиперболическим в точке
отрицателен, а все остальные положительны (или наоборот), то д.у. (1) называют гиперболическим в точке 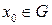 .
.
В случае, когда 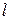 (
( ) коэффициентов
) коэффициентов  положительны, а остальные
положительны, а остальные 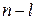 отрицательны, то д.у. (1) в точке
отрицательны, то д.у. (1) в точке  называют ультрагиперболическим.
называют ультрагиперболическим.
Если хотя бы один из коэффициентов  , то д.у. в точке
, то д.у. в точке  называют параболическим. При этом, если остальные коэффициенты одного знака, то д.у. (1) в точке
называют параболическим. При этом, если остальные коэффициенты одного знака, то д.у. (1) в точке  называют параболо-эллиптическим; если же остальные коэффициенты имеют разные знаки, то д.у. (1) в точке
называют параболо-эллиптическим; если же остальные коэффициенты имеют разные знаки, то д.у. (1) в точке  называют параболо-гиперболическим.
называют параболо-гиперболическим.
Говорят, что в области  своего задания уравнение (1) является уравнением эллиптического, гиперболического и параболического типа, если оно соответственно эллиптично, гиперболично и параболично в каждой точке области
своего задания уравнение (1) является уравнением эллиптического, гиперболического и параболического типа, если оно соответственно эллиптично, гиперболично и параболично в каждой точке области  .
.
|
|
|
Если в различных частях области  уравнение (1) принадлежит различным типам, то говорят, что уравнение (1) является уравнением смешанного типа в данной области
уравнение (1) принадлежит различным типам, то говорят, что уравнение (1) является уравнением смешанного типа в данной области  .
.
Пример 1. Рассмотрим 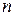 -мерное уравнение Лапласа
-мерное уравнение Лапласа
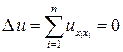 , (4)
, (4)
которое определено во всем пространстве  .
.
Составим соответствующую квадратичную форму
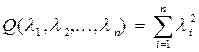 ,
,
так как 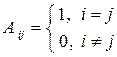 и поэтому
и поэтому 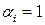 ,
, 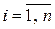 . Следовательно, уравнение (4) является эллиптическим во всем пространстве
. Следовательно, уравнение (4) является эллиптическим во всем пространстве  .
.
Пример 2. Рассмотрим 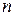 -мерное волновое уравнение
-мерное волновое уравнение
ð 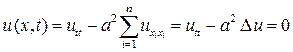 , (5)
, (5)
которое определено в пространстве 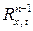 ,
, 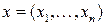 .
.
Составим соответствующую квадратичную форму
 .
.
После замены 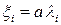 ,
, 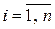 ,
, 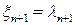 квадратичная форма
квадратичная форма 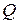 примет вид
примет вид
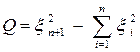 .
.
Здесь один коэффициент положительный, все остальные коэффициенты отрицательные. Следовательно, уравнение (5) является уравнением гиперболического типа во всем пространстве  .
.
Пример 3. Рассмотрим 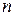 -мерное уравнение теплопроводности, заданное в
-мерное уравнение теплопроводности, заданное в 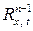 :
:
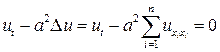 . (6)
. (6)
Составим квадратичную форму
 ,
,
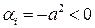 ,
, 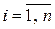 ,
, 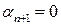 .
.
Таким образом, уравнение (6) является уравнением параболического типа во всем пространстве  .
.
В случае уравнения второго порядка от двух переменных 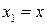 и
и 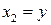 , уравнение (1) примет вид
, уравнение (1) примет вид
 . (7)
. (7)
Соответствующая квадратичная форма равна
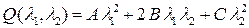 . (8)
. (8)
Если 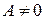 , то квадратичную форму (8) можно представить в виде
, то квадратичную форму (8) можно представить в виде
 . (9)
. (9)
Поэтому квадратичная форма (8) положительна или отрицательно определена в точке  , если
, если 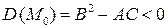 . В самом деле, полагая в (9)
. В самом деле, полагая в (9)
 ,
,  ,
,
получим

Следовательно, если  , то д.у. (7) в точке
, то д.у. (7) в точке 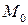 принадлежит эллиптическому типу.
принадлежит эллиптическому типу.
Пусть 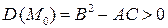 . Тогда после замены
. Тогда после замены
 ,
, 
квадратичная форма (9) принимает вид

т.е. один из коэффициентов  ,
, 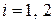 , формы
, формы 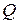 положителен, а другой отрицателен. Таким образом, в точке
положителен, а другой отрицателен. Таким образом, в точке 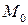 д.у. (7) принадлежит гиперболическому типу.
д.у. (7) принадлежит гиперболическому типу.
Пусть  . Тогда заменой
. Тогда заменой
 ,
, 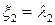
квадратичная форма (9) приводится к виду
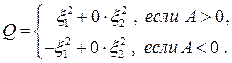
Отсюда видно, что один из двух коэффициентов формы 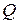 равен нулю, а другой отличен от нуля. Значит д.у. (7) в точке
равен нулю, а другой отличен от нуля. Значит д.у. (7) в точке 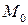 является уравнением параболического типа.
является уравнением параболического типа.
|
|
|
Поэтому в случае д.у. (7) классификация уравнения определяется знаком дискриминанта 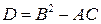 .
.
Определение 2. Если в точке  :
:
1)  , то в этой точке д.у. (7) называется уравнением эллиптического типа;
, то в этой точке д.у. (7) называется уравнением эллиптического типа;
2)  , то в этой точке д.у. (7) называется уравнением параболического типа;
, то в этой точке д.у. (7) называется уравнением параболического типа;
3) 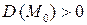 , то в этой точке д.у. (7) называется уравнением гиперболического типа.
, то в этой точке д.у. (7) называется уравнением гиперболического типа.
Пример 4. Определить тип д.у. в ч.п.
а)  ,
,
б)  ,
,
в)  ,
,
г)  .
.
Решение. Прежде всего заметим, что в примерах а) – в) коэффициенты д.у. в ч.п. при производных второго порядка постоянные, поэтому тип этих уравнений определяется во всем пространстве.
а). Согласно изложенной выше теории составим соответствующую данному уравнению квадратичную форму
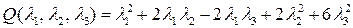 (10)
(10)
и методом выделения полных квадратов приведем ее к каноническому виду
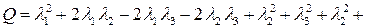
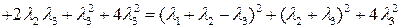 .
.
Полагая здесь
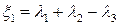 ,
, 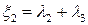 ,
,  ,
,
получим
 ,
,
следовательно, д.у. а) в 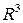 является уравнением эллиптического типа. В этом случае можно было воспользоваться критерием Сильвестра о положительной определенности квадратичных форм. Для этого для данного д.у. составим аналог матрицы (*) и вычислим все главные диагональные миноры
является уравнением эллиптического типа. В этом случае можно было воспользоваться критерием Сильвестра о положительной определенности квадратичных форм. Для этого для данного д.у. составим аналог матрицы (*) и вычислим все главные диагональные миноры
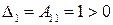 ,
, 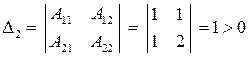 ,
, 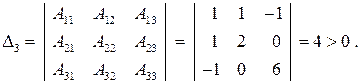
Поскольку все определители 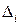 ,
, 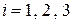 , положительны, то в силу теоремы Сильвестра форма (10) положительно определена, поэтому данное д.у. является эллиптическим во всем пространстве.
, положительны, то в силу теоремы Сильвестра форма (10) положительно определена, поэтому данное д.у. является эллиптическим во всем пространстве.
б). В этом случае форма имеет вид

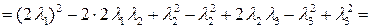
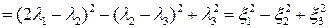 ,
,
где  ,
,  ,
, 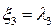 . Отсюда видим, что данное д.у. является гиперболическим во всем пространстве.
. Отсюда видим, что данное д.у. является гиперболическим во всем пространстве.
в). Составим соответствующую квадратичную форму и приведем ее к каноническому виду
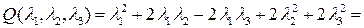
 ,
,
где 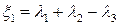 ,
, 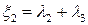 ,
, 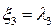 . Один из коэффициентов канонической формы равен нулю, а остальные отличны от нуля. Следовательно, данное д.у. является параболическим в
. Один из коэффициентов канонической формы равен нулю, а остальные отличны от нуля. Следовательно, данное д.у. является параболическим в 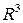 .
.
г). Для данного уравнения  ,
,  ,
,  , поэтому
, поэтому  . Следовательно, при
. Следовательно, при 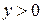 уравнение принадлежит эллиптическому типу, при
уравнение принадлежит эллиптическому типу, при  оно является уравнением гиперболического типа, а при
оно является уравнением гиперболического типа, а при 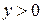 (
( ) становится уравнением параболического типа. Таким образом, данное уравнение на плоскости
) становится уравнением параболического типа. Таким образом, данное уравнение на плоскости 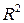 является уравнением смешанного типа.
является уравнением смешанного типа.
§ 3. Приведение к каноническому виду дифференциального уравнения второго порядка от двух независимых переменных.
Понятие характеристики
Рассмотрим д.у. в ч.п. второго порядка, линейное относительно старших производных
|
|
|
 , (1)
, (1)
в области 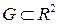 , где
, где 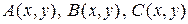 – заданные дважды непрерывно дифференцируемые в
– заданные дважды непрерывно дифференцируемые в  функции,
функции,  – заданная функция от своих аргументов.
– заданная функция от своих аргументов.
Будем предполагать, что коэффициенты 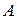 ,
, 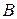 и
и  не обращаются одновременно в нуль в области
не обращаются одновременно в нуль в области  , т.е. при любом
, т.е. при любом 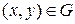
 .
.
Введем вместо переменных 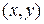 новые независимые переменные
новые независимые переменные 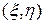 :
:
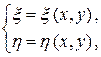 (2)
(2)
где  и
и  – дважды непрерывно дифференцируемые функции в области
– дважды непрерывно дифференцируемые функции в области  , причем якобиан отображения (2) отличен от нуля в области
, причем якобиан отображения (2) отличен от нуля в области  :
:
 . (3)
. (3)
Тогда систему (2) можно однозначно разрешить относительно  и
и 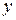 в некоторой области точек
в некоторой области точек 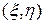 . При этом полученные функции
. При этом полученные функции 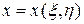 ,
, 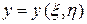 будут также дважды непрерывно дифференцируемыми функциями от
будут также дважды непрерывно дифференцируемыми функциями от 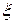 и
и  .
.
Далее будем считать, что функция  . Вычислим производные функции
. Вычислим производные функции 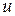 по новым переменным
по новым переменным 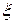 и
и  . На основании теоремы о дифференцировании сложной функции имеем:
. На основании теоремы о дифференцировании сложной функции имеем:
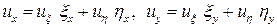 ,
,
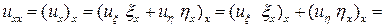
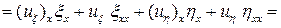
 ,
,


 ,
,
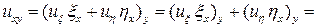

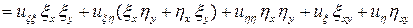 .
.
Итак, производные функции 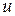 выражаются через производные от новых переменных
выражаются через производные от новых переменных 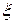 и
и  по следующим формулам:
по следующим формулам:
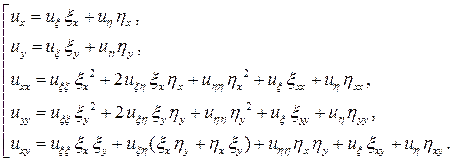 (4)
(4)
Подставляя значения производных из формулы (4) в уравнение (1), получим
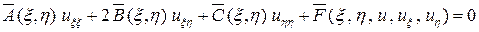 , (5)
, (5)
где
 (6)
(6)
Непосредственной подстановкой нетрудно показать, что
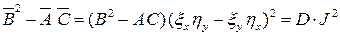 . (7)
. (7)
Из равенства (7) видно, что преобразование (2) и (3) независимых переменных не меняет типа уравнения (1).
Поставим следующую задачу: как выбрать переменные 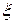 и
и  , чтобы уравнение (1) в этих переменных имело наиболее простую форму?
, чтобы уравнение (1) в этих переменных имело наиболее простую форму?
Для решения данной задачи попытаемся выбрать функции 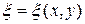 и
и 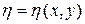 , так чтобы обратить в нуль некоторые из коэффициентов
, так чтобы обратить в нуль некоторые из коэффициентов 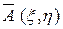 ,
,  ,
,  . Заметим, что вопрос об обращении в нуль коэффициентов
. Заметим, что вопрос об обращении в нуль коэффициентов 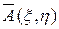 и
и  эквивалентен разрешимости д.у. в ч.п. первого порядка
эквивалентен разрешимости д.у. в ч.п. первого порядка
 . (8)
. (8)
Лемма. Пусть функция  (
( ) и
) и  в области
в области 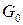 (или
(или 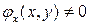 в области
в области 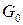 ). Функция
). Функция 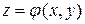 является частным решением уравнения (8), тогда и только тогда, когда равенство
является частным решением уравнения (8), тогда и только тогда, когда равенство  , где
, где 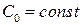 , представляет собой общий интеграл обыкновенного д.у.
, представляет собой общий интеграл обыкновенного д.у.
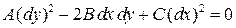 . (9)
. (9)
Обыкновенное д.у. (9) называется характеристическим уравнением для уравнения (1), а его решения – характеристиками уравнения (1).
Рассмотрим три случая в зависимости от типа уравнения (1).
Первый случай. Пусть 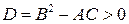 в области
в области  . Тогда в этой области уравнение (1) является уравнением гиперболического типа. Рассмотрим произвольную точку
. Тогда в этой области уравнение (1) является уравнением гиперболического типа. Рассмотрим произвольную точку 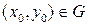 , в окрестности которой уравнение (1) будем приводить к каноническому виду. В этой точке
, в окрестности которой уравнение (1) будем приводить к каноническому виду. В этой точке  или
или 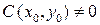 , в противном случае уравнение (1) уже имеет канонический вид. Пусть
, в противном случае уравнение (1) уже имеет канонический вид. Пусть  . Поскольку
. Поскольку 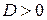 , тогда уравнение (9) распадается на совокупность двух обыкновенных д.у. первого порядка
, тогда уравнение (9) распадается на совокупность двух обыкновенных д.у. первого порядка
|
|
|
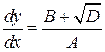 , (11)
, (11)
 . (12)
. (12)
Поскольку правые части обыкновенных д.у. (11) и (12) имеют по условию непрерывные частные производные до 2-го порядка включительно и  в окрестностях точки
в окрестностях точки  , то из теоремы существования и единственности решения задачи Коши для обыкновенных д.у. 1-го порядка следует существование общих интегралов:
, то из теоремы существования и единственности решения задачи Коши для обыкновенных д.у. 1-го порядка следует существование общих интегралов:
 ,
, 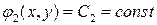 , (13)
, (13)
уравнений (11) и (12) и их левые части имеют непрерывные частные производные до второго порядка в окрестности точки  .
.
Для уравнений гиперболического типа общие интегралы (13) вещественны и различны. Значит, уравнения гиперболического типа имеют два различных семейства вещественных характеристик.
В преобразовании (2) положим, что
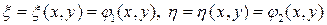 ,
,
где функции 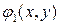 и
и 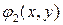 в силу леммы являются соответственно непрерывно дифференцируемыми решениями уравнения (8). Тогда в силу равенств (6) в уравнении (5)
в силу леммы являются соответственно непрерывно дифференцируемыми решениями уравнения (8). Тогда в силу равенств (6) в уравнении (5) 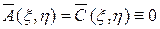 . Коэффициент
. Коэффициент 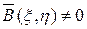 в окрестности точки
в окрестности точки  , так как в противном случае либо
, так как в противном случае либо  , либо
, либо 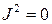 . Разделив на коэффициент
. Разделив на коэффициент 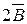 уравнение (5), получим
уравнение (5), получим
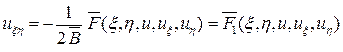 . (14)
. (14)
Уравнение (14) есть канонический вид уравнений гиперболического типа (1).
При 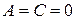 уравнение (1) уже имеет канонический вид (14).
уравнение (1) уже имеет канонический вид (14).
Если уравнение (1) является линейным относительно производных первого порядка и самой функции 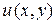 , то преобразованное уравнение так же будет линейным
, то преобразованное уравнение так же будет линейным
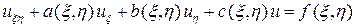 .
.
Второй случай. Пусть 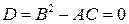 в области
в области  . Тогда в области
. Тогда в области  уравнение (1) является уравнением параболического типа. Так как по предположению коэффициенты
уравнение (1) является уравнением параболического типа. Так как по предположению коэффициенты 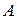 ,
, 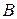 и
и  уравнения (1) не обращаются одновременно в нуль, то в силу условия
уравнения (1) не обращаются одновременно в нуль, то в силу условия  следует, что в каждой точке области
следует, что в каждой точке области  один из коэффициентов
один из коэффициентов 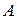 и
и  отличен от нуля. Не нарушая общности можно считать, что
отличен от нуля. Не нарушая общности можно считать, что 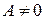 в точке
в точке 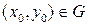 , в окрестности
, в окрестности 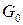 которой будем приводить уравнение (1) к каноническому виду. В этом случае оба уравнения (11) и (12) совпадают и обращаются в уравнение
которой будем приводить уравнение (1) к каноническому виду. В этом случае оба уравнения (11) и (12) совпадают и обращаются в уравнение
 .
.
Для уравнения параболического типа имеется только одно семейство вещественных характеристик  . В преобразовании (2) положим
. В преобразовании (2) положим  , где
, где  и есть решение уравнения (8). Возьмем за функцию
и есть решение уравнения (8). Возьмем за функцию 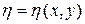 любую дважды непрерывно дифференцируемую функцию так, чтобы якобиан в окрестности
любую дважды непрерывно дифференцируемую функцию так, чтобы якобиан в окрестности 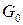 точки
точки  был отличен от нуля:
был отличен от нуля: 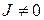 . В уравнении (5) коэффициент
. В уравнении (5) коэффициент  , так как
, так как  является решением д.у. (8). Тогда из равенства (7) следует, что коэффициент при частной производной
является решением д.у. (8). Тогда из равенства (7) следует, что коэффициент при частной производной  также равен нулю, т.е.
также равен нулю, т.е.  . Коэффициент
. Коэффициент 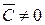 в
в 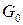 . Если
. Если 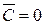 в некоторой точке
в некоторой точке 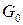 , то из (6) с учетом
, то из (6) с учетом  , найдем (для определенности
, найдем (для определенности 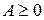 и
и 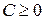 )
)
 (*)
(*)
Поскольку определитель системы (*)
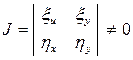 ,
,
то система (*) имеет только нулевое решение  . Тогда
. Тогда  что противоречит условию
что противоречит условию 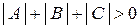 в
в 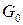 . Разделив на
. Разделив на 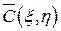 уравнение (5), получим
уравнение (5), получим
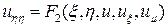 . (15)
. (15)
Выражение (15) является каноническим видом уравнений параболического типа.
Третий случай. Пусть  в области
в области  . Тогда в этой области уравнение (1) является уравнением эллиптического типа. Будем считать, что коэффициенты
. Тогда в этой области уравнение (1) является уравнением эллиптического типа. Будем считать, что коэффициенты  и
и  уравнения (1) являются аналитическими функциями в области
уравнения (1) являются аналитическими функциями в области  . Тогда правые части уравнения (11) и (12) также являются аналитическими функциями от переменных
. Тогда правые части уравнения (11) и (12) также являются аналитическими функциями от переменных  и
и 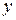 . По теореме Коши – Ковалевской уравнение (11) имеет аналитическое решение
. По теореме Коши – Ковалевской уравнение (11) имеет аналитическое решение
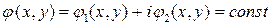
в малой окрестности точки 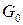 такой, что
такой, что  и
и
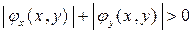 в
в 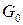 .
.
В преобразовании (2) положим  и
и 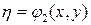 , причем они удовлетворяют условию
, причем они удовлетворяют условию
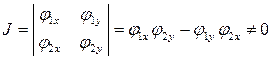 в
в 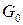 .
.
Действительно, допустим, что в некоторой точке 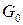
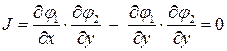 .
.
Тогда будем иметь
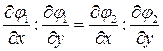 или
или  . (16)
. (16)
Поскольку функция  является аналитической в области
является аналитической в области 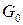 , то для нее справедливы условия Коши – Римана:
, то для нее справедливы условия Коши – Римана:
 ,
, 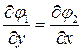 .
.
Отсюда
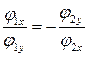 ,
,
что противоречит равенству (16). Полученное противоречие доказывает, что якобиан 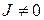 в
в 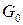 .
.
Итак, имеем 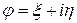 и подставляя данное равенство в д.у.(8), получим тождество:
и подставляя данное равенство в д.у.(8), получим тождество:
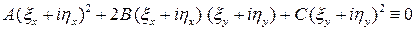 .
.
Разделив здесь вещественную и мнимую части тождества, будем иметь:
 ,
,
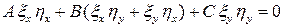 .
.
Из последних равенств следует, что  и
и  , причем
, причем  , в противном случае получим противоречие с равенством (7).
, в противном случае получим противоречие с равенством (7).
Разделив уравнение (5) на коэффициент 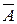 , получим:
, получим:
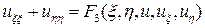 . (17)
. (17)
Выражение (17) является каноническим видом уравнений эллиптического типа.
При 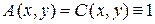 и
и  уравнение (1) уже имеет канонический вид (17).
уравнение (1) уже имеет канонический вид (17).
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 1090; Нарушение авторских прав?; Мы поможем в написании вашей работы!