Основных начально-граничных задач

Вывод уравнения теплопроводности. Постановка

Рассмотрим твердое тело, температура которого в каждой точке определяется функцией в момент времени . Если различные части тела находятся при различной температуре, то в теле будут происходить движение тепла от более нагретых частей к менее нагретым частям тела. Вывод уравнения распространения тепла базируется на законе Фурье, согласно которому количество тепла 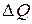, проходящее за время 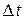через малую площадку 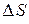, находящуюся внутри рассматриваемого тела, определяется формулой

, (1)

где 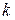– коэффициент теплопроводности, 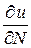– производная по нормали к площадке 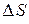и она определяется формулой

,

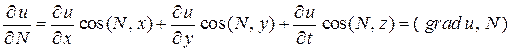т.е. производная по нормали представляет собой скалярное произведение двух векторов:

,

,

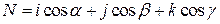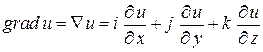где – направляющие единичные векторы соответственно осей координат – углы между нормалью с осями координат.

В формуле (1) знак " – " означает, что тепло переходит от более нагретых точек к менее нагретым. В дальнейшем предположим, что тело изотропно, это означает, что коэффициент теплопроводности 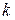зависит только от 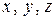и не зависит от 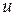и 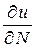. Если тело анизотропно, то .

z

Для вывода уравнения распределения тепла в изотропном теле выделим внутри тела достаточно малый параллелепипед (см. рис. 3)

h

x

.

		(x, y, z)

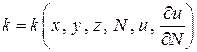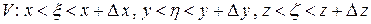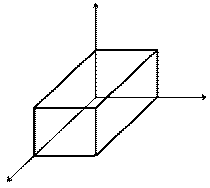
Рис. 3

Составим для параллелепипеда 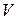тепловой баланс. Через площадку по закону (1) входит за время 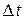количество тепла:

.

Через площадку 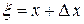выходит следующее количество тепла

.

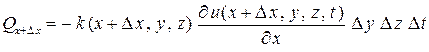Тогда остающееся количество тепла в теле 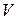вдоль оси равно

.

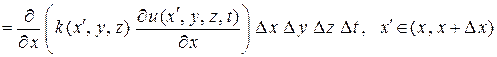Аналогично вычисляется приток тепла через другие грани тела :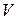

,

.

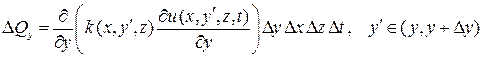Тогда общее количество теплоты, притекающее в тело 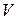за промежуток времени 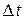, равняется

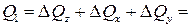
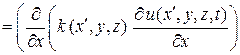
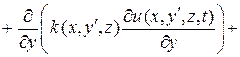
. (2)

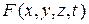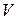Предположим, что внутри рассматриваемого тела имеются источники тепла. Пусть – непрерывная плотность тепла в единицу времени в единице объема тела. Тогда количество тепла , образующееся в теле за счет внешних источников тепла за время 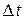, равно

. (3)

С другой стороны для изменения температуры тел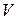а на 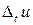за промежуток времени 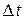нужно затратить количество тепла

,

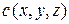где – плотность тела, – теплоемкость тела, которые будем считать непрерывными функциями. На основании теоремы Лагранжа имеем

. (4)

Составим уравнение баланса выделенного тепла для тела 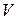. Ясно, что . Тогда с учетом выражений (2) – (4) получим

.

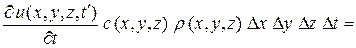
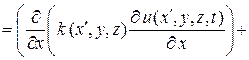
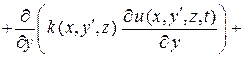
Сократив полученное равенство на 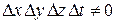и переходя к пределу при , , 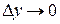, , 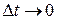будем иметь

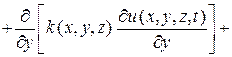
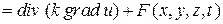, (5)

где дивергенция вектор – функции

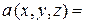
определяется формулой

.

Уравнение (5) называется уравнением теплопроводности неоднородного изотропного тела.

Если тело однородное, то , , ,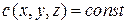

,

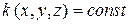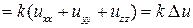где называется оператором Лапласа. Тогда уравнение (5) примет вид

,

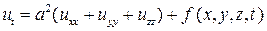где , .

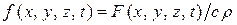Если в рассматриваемом однородном теле нет внешних источников тепла, т.е. 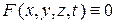, то получим однородное уравнение теплопроводности

.

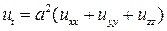В частности, когда температура 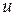зависит только от координат , что, например, имеет место при распределении тепла в тонкой однородной пластинке, то уравнение (5) переходит в следующее уравнение

.

Для тела линейного размера, например, для однородного стержня уравнение теплопроводности имеет вид

.

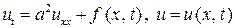Дата добавления: 2014-01-07