Правила перевода

Алфавит десятичной, двоичной, восьмеричной и шестнадцатеричной систем счисления

Двоичная система счисления

Десятичная система счисления

Какие позиционные системы счисления используются сейчас?

Шестидесятеричная система счисления

Следующая позиционная система счисления была придумана еще в Древнем Вавилоне, причем вавилонская нумерация была шестидесятеричная, т.е. в ней использовалось шестьдесят цифр.

В более позднее время использовалась арабами, а также древними и средневековыми астрономами. Шестидесятеричная система счисления, как считают исследователи, являет собой синтез уже вышеупомянутых пятеричной и двенадцатеричной систем.

В настоящее время наиболее распространены десятичная, двоичная, восьмеричная и шестнадцатеричная системы счисления.

Двоичная, восьмеричная (в настоящее время вытесняется шестнадцатеричной) и шестнадцатеричная система часто используется в областях, связанных с цифровыми устройствами, программировании и вообще компьютерной документации.

Современные компьютерные системы оперируют информацией представленной в цифровой форме. Числовые данные преобразуются в двоичную систему счисления.

Десятичная система счисления – позиционная система счисления по основанию 10.

Предполагается, что основание 10 связано с количеством пальцев рук у человека.

Наиболее распространённая система счисления в мире.

Для записи чисел используются символы 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, называемые арабскими цифрами.

Двоичная система счисления – позиционная система счисления с основанием 2. Используются цифры 0 и 1.

Двоичная система используется в цифровых устройствах, поскольку является наиболее простой и удовлетворяет требованиям:

· Чем меньше значений существует в системе, тем проще изготовить отдельные элементы.

· Чем меньше количество состояний у элемента, тем выше помехоустойчивость и тем быстрее он может работать.

· Простота создания таблиц сложения и умножения – основных действий над числами

Десятичная: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9

Двоичная: 0, 1

Восьмеричная: 0, 1, 2, 3, 4, 5, 6, 7

Шестнадцатеричная: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F

Правила перевода чисел из десятичной системы в двоичную:

§ целая и дробная часть переводятся порознь,

§ для перевода целой части числа ее необходимо разделить на основание системы, т.е. на 2 и продолжить делить частные от деления до тех пор, пока частное не станет равным 0,

§ значения получившихся остатков, взятые в обратной последовательности образуют искомое двоичное число.

Например: 25₍₁₀₎ = 11001₍₂₎

25 / 2 = 12 остаток (1)

12 / 2 = 6 (0)

6 / 2 = 3 (0)

3 / 2 = 1 (1)

1 / 2 = 0 (1)

Для перевода дробной части надо умножить ее на 2. Целая часть произведения будет первой цифрой числа в двоичной системе. Затем дробную часть у полученного результата вновь умножают на 2 и т.д.

Например: 0,73 ₍₁₀₎ = 0,1011₍₂₎

0,73 * 2 = 1,46 целая часть (1)

0,46 * 2 = 0,92 (0)

0,92 * 2 = 1,84 (1)

0,84 * 2 = 1,68 (1)

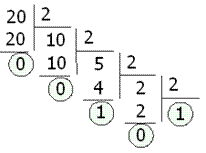Перевод из десятичной системы счисления в систему счисления с основанием p осуществляется последовательным делением десятичного числа и его десятичных частных на p, а затем выписыванием последнего частного и остатков в обратном порядке.

Чтобы перевести число из позиционной системы счисления с основанием p в десятичную, надо представить это число в виде суммы степеней p и произвести указанные вычисления в десятичной системе счисления.

1101 (2) =1*23 + 1*22+ 0*21 + 1*20

341,5 (8) = 3*82 + 4*81 + 1*80 5*8–1

A1F,4 (16) = 10*162 + 1*161 +15*160 + 4*16–1

4602₍₇₎=4*7³+6*7²+0*7¹+2*7⁰=1668₍₁₀₎.

Дата добавления: 2014-01-07